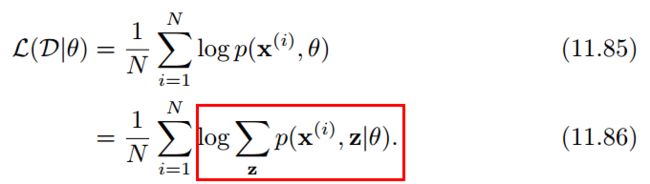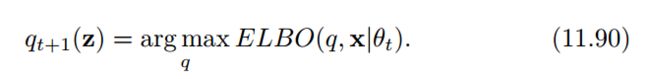概率图模型学习问题
图模型的学习可以分为两部分:
一是网络结构学习,即寻找最优的网络结构。网络结构学习一般比较困难,一般是由领域专家来构建。
二是网络参数估计,即已知网络结构,估计每个条件概率分布的参数。
不含隐变量的参数估计
如果图模型中不包含隐变量,即所有变量都是可观测的,那么网络参数一般可以直接通过最大似然来进行估计。
含隐变量的参数估计
如果图模型中包含隐变量,即有部分变量是不可观测的,就需要用 EM算法进行参数估计。
带隐变量的贝叶斯网络。图中的矩形表示其中的变量重复 N 次。
EM 算法
EM 算法是含隐变量图模型的常用参数估计方法,通过迭代的方法来最大化边际似然。 EM算法具体分为两个步骤: E步和 M步。这两步不断重复,直到收敛到某个局部最优解。
EM算法的应用例子:高斯混合模型。
高斯混合模型(Gaussian Mixture Model, GMM)是由多个高斯分布组成的模型,其密度函数为多个高斯密度函数的加权组合。
在一个包含隐变量的图模型中,令 X定义可观测变量集合,令 Z定义隐变量集合,一个样本 x的边际似然函数(marginal likelihood)为
边 际 似 然 也 称 为 证 据(evidence)。
给定 N 个训练样本D = {x(i)}, 1 ≤ i ≤ N,其训练集的对数边际似然为
通过最大化整个训练集的对数边际似然L(D|θ),可以估计出最优的参数θ∗。然而计算边际似然函数时涉及 p(x)的推断问题,需要在对数函数的内部进行求和(或积分)。这样,当计算参数 θ 的梯度时,
这个求和操作依然存在。除非p(x, z|θ)的形式非常简单,否则这个求和难以直接计算。 因此,含有隐变量时,直接进行最大似然估计行不通(如何计算log p(x|θ)成为关键)。
为了计算log p(x|θ),我们引入一个额外的变分函数 q(z), q(z)为定义在隐变量 Z上的分布。样本 x的对数边际似然函数改写为
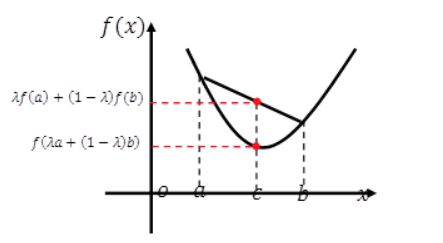
Jensen不等式:即对于凸函数 g,有g (E[X]) ≤ E [g(X)]。
其中ELBO(q, x|θ)为对数边际似然函数log p(x|θ)的下界,称为证据下界(EvidenceLower Bound, ELBO)。
由 Jensen不等式的性质可知,仅当q(z) = p(z|x, θ)时, 对数边际似然函数log p(x|θ)和其下界 ELBO(q, x|θ)相等,
将最大化对数边际似然函数 log p(x|θ)的过程可以分解为两个步骤:
- (1)固定参数 θ ,先找到近似分布 q(z)使得 log p(x|θ) = ELBO(q, x|θ);
- (2)固定分布 q(z),再寻找参数 θ 最大化 ELBO(q, x|θ)。
这就是期望最大化(Expectation-Maximum, EM)算法。
EM 算法是含隐变量图模型的常用参数估计方法,通过迭代的方法来最大化边际似然。 EM算法具体分为两个步骤: E步和 M步。这两步不断重复,直到收敛到某个局部最优解。
在第 t步更新时, E步和 M步分布为:
E步(Expectation step)
固定参数θt,找到一个分布q(z)使得ELBO(q, x|θt)最大(即等于log p(x|θt))。
根据 Jensen不等式的性质, 仅当q(z) = p(z|x, θt)时, ELBO(q, x|θt)最大(ELBO(q, x|θt) = log p(x|θt))。
因此, E步可以看作是一种推断问题,即计算后验概率 p(z|x, θt)。
M步(Maximization step)
固定 qt+1(z),找到一组参数θ 使得证据下界ELBO最大,即
这一步可以看作是全观测变量图模型(不含隐变量)的参数估计问题,可以使用极大似然估计进行参数估计。
可以看到,每经过一次迭代对数边际似然都在增加,log p(x|θt+1) ≥ log p(x|θt)。
在 E 步中,最理想的变分分布 q(z) 是等于后验分布 p(z|x, θ)。而后验分布p(z|x, θ)需要进行推断得到。如果 z是有限的一维离散变量(比如混合高斯模型),计算起来还比较容易。
否则, p(z|x, θ)一般情况下很难计算。因此需要通过近似推断的方法来进行估计,比如变分自编码器。
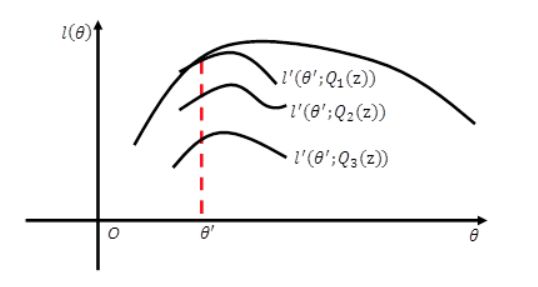
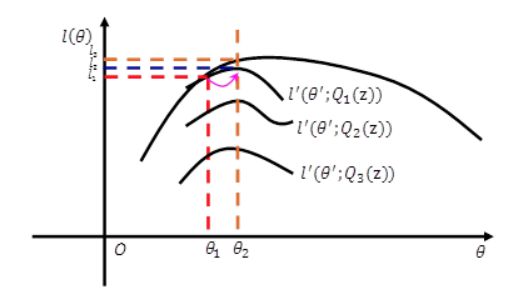
几何解释
EM算法本质是一个不断取最优下界,抬高下界的过程。
Jensen不等式的几何解释
在E步固定模型参数,改变q(z)可以得到一组下界,当q取后验概率时得到最优下界(Jensen不等式)。
在M步将q固定,对模型参数优化得到局部最优值。
反复迭代最终得到收敛解(见收敛性证明),即最大似然值。
因此,EM算法本质是一个不断取最优下界,抬高下界的过程。通过构造下界,并抬高下界的方式对无法直接优化的边际似然进行间接优化。