题目大意
给定一个 $n$ 个点 $m$ 条边的带正权无向图。要求找一条路径满足:
它是一条简单路径
它是一条严格次短路
对于任何一条可能存在于最短路上的边,不能包含它的反向边。
不存在这条路径输出 - 1。
题解
良心的最短路性质题,涵盖了大部分最短路径树和最短路径图上的常用性质。
然后开始讲正题。
最短路径图的基本性质
将 $d\left (u, v \right)$ 记为点 $u$ 到点 $v$ 的最短路的长度。
记 $d_{s}\left (x \right ) = d\left (s, x \right ), d_{t}\left (x \right ) = d\left (x, t \right )$。
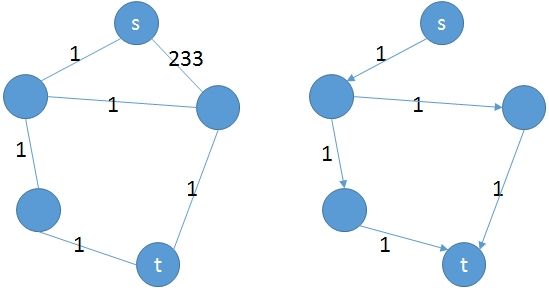
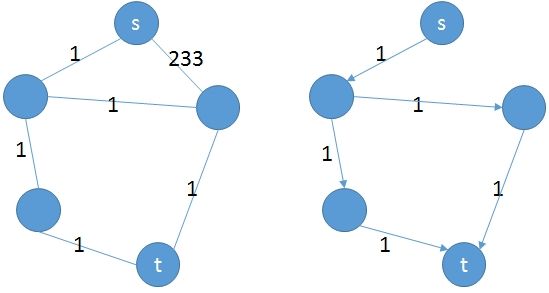
最短路径图是 $s$ 到 $t$ 的所有最短路径的并集。
举个例子有助于说明:
左边为原图,右边为最短路径图。
注意 最短路径图是一个有向图。
这里将原图记为 $G = (V, E)$,最短路径图记为 $G* = (V*, E*)$。
最短路径图的基本性质 I(定义 1.1)
对于任意 $e \in E*$,若 $e = (u, v)$,那么 $d_{s}(u) + w (e) + d_{t}(v) = d (s, t)$。
显然最短路径图一定是一个 DAG。
最短路径图的基本性质 II(定理 1.1)
对于任意 $x \in V*$,那么有 $d_{s}(x) + d_{t}(x) = d (s, t)$。
证明 如果 $s = x$,那么结论显然成立。
现在考虑 $s \neq x$ 的情况。暂时记 $L = d (s, t)$
由最短路径图的定义可知 $d_{s}(x) \geqslant L - d_{t}(x)$。因为 $x$ 不是起点,所以必然存在一个前驱 $x'$。
根据基本性质 I 有 $d_{s}(x') + w (x', x) + d_{t}(x) = L$。由 $d_{s}(x)$ 的定义可知 $d_{s}(x) \leqslant d_{s}(x') + w (x, x') = L - d_{t}(x)$。
所以 $d_{s}(x) = L - d_{t}(x)$。
因此定理得证。
最短路径图的基本性质 III(推论 1.2)
对于 $e = (x, y) \in E*$,那么有 $d_{s}(x) + w (x, y) = d_{s}(y)$。
证明 根据定理 1.1 有 $d_{s}(y) = d (s, t) - d_{t}(y)$。根据定义 1.1 有 $d_{s}(x) + w (x, y) = d (s, t) - d_{t}(y)$。然后定理得证。
最短路径图的基本性质 IV(推论 1.3)
如果最短路径图中存在一条 $x$ 到 $y$ 的简单路径,那么 $d_{s}(x) + l (P*(x, y)) + d_{t}(y) = L$。其中 P*(x, y) 表示一条在 $G*$ 上的路径,l (P*(x, y)) 表示这条路径的长度。
重复使用推论 1.2 可以得到 $d_{s}(x) + l (P*(x, y)) = d_{s}(y)$。然后根据定理 1.1 易证。详细证明留给读者。
最短路径图的基本性质 V(推论 1.4)
最短路径图中一条 $x$ 到 $y$ 的简单路径,对应原图中一条 $x$ 到 $y$ 的最短路。
有了推论 1.3 就可以使用反证法。详细证明留给读者。同时可以推出上面的 $ l (P*(x, y)) = d (x, y)$。
定理 1.5
若 $x, y \in V*$,且满足 $x \neq y, d_{s}(x) \leqslant d_{x}(y)$,那么在 $G*$ 中 $s$ 到 $x$ 的最短路与 $y$ 到 $t$ 的最短路不相交。
证明 根据最短路径图的定义(定义 1.1)可知,$s$ 到 $x$ 的过程中 $d_{s}(x')$ 递增,$y$ 到 $t$ 的过程中 $d_{s}(y')$ 递增。又因为 $x \neq y, d_{s}(x) \leqslant d_{x}(y)$,所以它们不相交。
定理 2
然后来讲一些约定吧。
正向边:对于一条有向边 $(u, v)$,它在 $E*$ 中,那么我们称它为一条正向边。
反向边:对于一条有向边 $(u, v)$,如果 $(v, u) \in E*$,那么我们称它为一条反向边。
内部边:正向边和反向边统称为内部边。
外部边:在 $E$ 中,但不属于 $E*$ 的边。
现在来明确一下约定路径的符号。
$P (u, v)$,表示一条 $u$ 到 $v$ 的路径。
$P*(u, v)$,表示一条在 $G*$ 中 $u$ 到 $v$ 的路径。
$P (x, y) + Q (y, z)$,表示一条沿着路径 $P$ 从 $x$ 走到 $y$ 的,然后沿着 $Q$,从 $y$ 走到 $z$ 的路径。
$P^{-1}(x, y)$,表示沿着路径 $P$ 的反向边(不是上面的定义的反向边),从 $y$ 到 $x$ 的一条路径。
$P^{0}(x', y')$,路径 $P$ 上,一条 $x'$ 到 $y'$ 的子路径。
$l (P)$,表示路径 $P$ 的长度。
设所求路径为 $S$。
外部路径:起点和终点在 $G*$ 中,经过的变都是外部边的一条简单路径。称起点是这条路径的拐出点,终点是这条路径的回归点。
定理 2.1
路径 $S$ 中存在至少 1 条外部路径。
证明 如果不包含外部路径,那么路径 $S$ 中的边都是正向边(因为不能走反向边)。由于 $G*$ 是一个 DAG,所以 $l (S) = d (s, t)$,不符合题目要求。
定理 2.2
路径 $S$ 的包含一条外部路径的拐出点为 $x$,回归点为 $y$,那么有 $d_{s}(x) \leqslant d_{s}(y)$。
证明:
假设结论不成立,那么有 $d_{s}(x) > d_{s}(y)$。
设 $S = P (s, x) + Q (x, y) + R (y, t)$。那么令 $U = P*(s, y) + Q^{-1}(x, y) + R*(x, t)$。因为路径 $Q$ 是一条简单路径,P * 和 R * 都是由正向边组成,根据定理 1..5 可得 P * 与 R * 不相交。所以 $U$ 是一条简单路径。
又因为 $U$ 包含了至少一条外部边,所以它不是最短路。因此是一条满足题目要求的路径。
又因为 $P*(s, y) < P*(s, x) \leqslant P (s, x), R*(x, t) < R*(y, t) \leqslant R (y, t), Q (x, y) = Q^{-1}(x, y)$,所以 $l (U) < l (S)$。
与 $S$ 的最优性矛盾。
定理 2.3
路径 $S$ 恰好包含一条外部路径。
证明:
假设包含的外部路径数目不是一条。
如果不包含外部路径,显然矛盾。
如果包含超过一条外部路径,设 $S = P*(s, x) + Q (x, y) + R (y, t)$,令 $U = P*(s, x) + Q (x, y) + R*(y, t)$,其中 $Q (x, y)$ 是一条外部路径。
根据定理 1.5 易证 $U$ 是一条简单路径,根据最短路径图的定义有 $R*(y, t) < R (y, t)$,因此 $l (U) < l (S)$,与 $S$ 的最优性矛盾。
最短路径树的性质
约定 $S$ 的拐出点为 $S$ 包含的外部路径的拐出点,它的回归点为它包含的外部路径的回归点。
定义 3.1
定义一棵以 $p$ 为根的最短路径树 $T_{p} = (V, E_{T})$ 是原图中以 $p$ 为根的一棵有向路径生成树。其中一条边 $e (v, u)$ 满足 $d (u, p) + w (e) = d (v, p)$。
由于下面只会用到 $T_{t}$,因此,以下可能会直接将它简记 $T$。
注意
这里的最短路径树是一个有向图。
所有有向边都指向根节点。
一张无向图的最短路径图唯一,但指定点的最短路径生成树可能不唯一。
然后再来定义定义子树。
定义 3.2
在以 $p$ 为根的最短路径生成树中:
点 $x$ 的子树,在 $T_{p}$ 点 $x$ 断掉点 $x$ 的唯一一条出边后,剩下的以 $x$ 为根的树是点 $x$ 的子树。记为 $T_{p}(x)$。
点 $x$ 的真子树,点 $x$ 的真子树是 $T_{p}(x)$ 的一个子图。在 $T_{p}(x)$ 中,存在于点 $x$ 的真子树的点,当且仅当它到 $x$ 的路径上不经过除了 $x$ 以外的任何属于 $G*$ 的点。也就是说一个 不是 $x$ 的点,但属于 $G*$,一定不存在于 $x$ 的真子树中。记为 $T*_{p}(x)$。
真子树的定义可能不是很好理解(再加上我语文不好),那么来举个栗子:
在第三幅图之后,边权都被省略。在第四幅图和第五幅图中间橙色点标出的是在 $G*$ 中的点。
下面有一个关于真子树的很基本的性质。
定理 3.1
对于任意 $x,y \in G*$,都有 $T*(x)\cap T*(y) = \varnothing $。
根据真子树的定义易证。
接下来再来约定一个记号。
$P_{T}(x, y)$,在树 $T_{t}$ 中,一条 $x$ 到 $y$ 的路径。
最短路径树中的基本性质(定理 3.2)
在最短路径树 $T_{t}$ 中,任意一个点 $x$ 到其祖先 $y$ 的一条简单路径,对应原图中一条 $x$ 到 $y$ 的最短路。
证明
证当 $y = t$ 时结论成立。
考虑 $y \neq t$ 的情况。
仍然假设不是最短路。那么存在一条更优的路径的从 $x$ 到 $y$,然后到 $t$ 的路径。与 $T_{t}$ 的定义矛盾。
因此定理得证。
注意到如果将这条路径反向,可以对应 $y$ 到 $x$ 在原图中的一条最短路。
定义 3.3
在 $T$ 中,$x$ 的真祖先是在路径 $P_{T}(x, t)$ 中,离 $x$ 最近的一个在 $G*$ 中的点。将它记作 $prt (x)$。
换一个说法就是沿着 $x$ 向它的出边走,直到遇到一个在 $G*$ 中的点。注意,它可能是 $x$ 也可能是 $t$。
设 $S$ 的拐出点为 $x$,回归点为 $z$,显然 $x \in T*(x), z \in T*(z)$,根据定理 3.1,那么 $T*(x)$ 和 $T*(z)$ 不存在交集。所以在 $S$ 上必然存在一条外部边 $(w, w')$ 使得 $w \in T*(x)$,且 $S^{0}(w', z)$ 中的各点均不在 $T*(x)$ 中。有一个很显然的事实是 $prt (w) = x$。
定理 3.3
$d_{s}(x) \leqslant d_{s}(prt(w'))$。
注意以下证明非常繁琐,请先喝口水再继续阅读。
证明
仍然假设结论不成立。那么有 $d_{s}(x) > d_{s}(prt (w'))$。所以 $d_{t}(x) < d_{t}(prt (w'))$。根据定理 2.2 有 $d_{s}(x) <= d_{s}(z)$,因此 $d_{s}(prt (w')) < d_{s}(z)$,所以 $prt (w') \neq z$。根据定理 3.1,可知,必然存在一条边 $(y, y')$ 使得 $y \in T*(prt (w'))$ 且 $S^{0}(y', z)$ 中的各点均不在 $T*(prt (w'))$。显然 $prt (w') = prt (y)$。
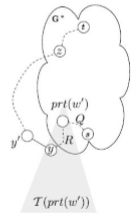
令 $Q = P*(s, prt (w')), R = P_{T}(prt (w'), y), P = Q + R + S^{0}(y, t)$(见下图)。
可以证明 $R$ 实际上是在 $T*(prt (w'))$ 中。假设路径上经过了其它的在 $G*$ 中的点,那么可知 $prt (y)$ 不等于 $prt (w')$,矛盾。
因为 $d_{s}(prt (w'))< d_{s}(z)$,根据定理 1.5 可知 $Q$ 不与 $S^{0}(z, t)$ 相交,又因为 $R$ 在 $T*(prt (w'))$ 中,所以经过的边都是外部边,所以 $P$ 中的内部边不相交。又因为 $S^{0}(y'. z)$ 是一条外部的简单路径,且不在 $T*(prt (w'))$。所以路径 $P$ 中的外部边不相交。因此路径 $P$ 是一条简单路径。(注意:这里的相交指的是存在环,而不是边与边存在公共点。)
又因为 $P$ 包含了至少一条外部边,所以 $P$ 是一条满足要求的路径(除了严格次短)。
因为 $S$ 是所求路径,所以有:
$l(S) \leqslant l(P)$
$l(S^{0}(s, x)) + l(S^{0}(x, y)) + l(S^{0}(y, t)) \leqslant l(Q) + l(R) + l(S^{0}(y, t))$
$l(S^{0}(s, x)) + l(S^{0}(x, y)) \leqslant l(Q) + l(R)$
$d_{s}(x) + l (S^{0}(x, y)) \leqslant d_{s}(prt (w')) + l (R)$(推论 1.4)
又因为 $prt (w') < d_{s}(x)$,所以 $l (S^{0}(x, y)) < l (R)$。
令 $U = S^{0}(x, y)^{-1} + P*(x, t)$。那么有:
$l(U) = l(S^{0}(x, y)^{-1}) + l(P*(x, y))\\=l(S^{0}(x,y)) + d_{t}(x)\\ 但是 $U$ 经过了至少一条外部边,所以有 $l (U) > l (P_{T}(y, t)) = d_{t}(y)$。但是刚刚却推出了与之矛盾的式子。 所以假设不成立,定理得证:$d_{s}(x) \leqslant (prt (w'))$。 必然存在一个满足所有条件的路径 S*,满足$S* = P_{T}(s, w) + (w, w') + P_{T}(w', t)$ 其中 $(w, w')$ 是定理 3.3 中涉及到的一条边。 证明 令 $Q = P_{T}(s, w), R = P_{T}(w', t)$,根据定理 3.1 易证 $S*$ 的外部边不相交,根据定理 3.3 和定理 1.5 易证 $S*$ 的内部边不会相交。又因为 $(w, w')$ 一定是一条外部边。所以 $S*$ 是一条简单路径但不是最短路径。 因为 $S$ 中包含至少一条非树边,然后用反证法易证存在一个 $S*$ 是满足题目所有要求的路径(除非原问题不存在解)。 于是定理 3.4 创造了无限可能。 我们只需要枚举一条非内部边,非树边 $e (x, y)$,且满足 $prt (x) \neq prt (y)$ 且 $d_s (prt (x)) \leqslant d_s (prt (y))$,然后用 $d_{s}(x) + w (e) + d_{t}(y)$ 去更新答案即可。 虽然证明很复杂,但是算法却异常简单。 转载至:http://www.cnblogs.com/yyf0309/p/8563071.html定理 3.4
做法
代码
![]()
![]()
1 #include