转载请注明出处:優YoU http://user.qzone.qq.com/289065406/blog/1305308196
为了简化说明,以三位数举例,
因为153、135、315、351、513、531的立方和都是一样的,均等于 1^3+3^3+5^3 = 153
而我们可以通过逐位检查 立方和153,发现1出现1次,3出现1次,5出现1次,而0~9中的其他数字均出现0次,出现的次数之和为3,刚好等于153的长度。
由此我们可以得到 利用枚举0~9各个数字出现的次数,得到水仙花数。
得到21位水仙花数的具体方法为:
通过10层循环,枚举0~9这10个数字出现的次数(每个数字都可能出现0~21次),当所有数字出现次数之和等于21时,说明这时数字的组合有可能为21位水仙花数。进而求出{[(每个数字的3次方)并分别乘以其出现的次数]后的值 之和sum}。例如 当我们枚举到数字6出现了5次,8出现16次 时,由于8+16=21,此时我们计算sum=6^21*5+8^21*16,检查得到的和sum的各个位,若恰好出现5个6和16个8,说明这种数字组合使得其和为水仙花数。
为了减少程序运行时间,我们可以先把0~9的21次方及其不同的出现次数的值利用另外的程序打表,数值存储到本程序的3维数组valus[i][j][k],表示数字i的21次方 乘以 j(出现次数)得到的值。需要用到这些值时可直接调用,此时我们只需要计算的是10个大数连加,无需计算求幂和乘法,大大节约时间。
valus[i][j][k]数组内容如下红色部分:
数字 出现次数
0 1 2 。。。。。。。 19 20 21
0 0^21 0^21*0 0^21*1 0^21*2 。。。。。。。 0^21*19 0^21*20 0^21*21
1 1^21 1^21*0 1^21*1 1^21*2 。。。。。。。 1^21*19 1^21*20 1^21*21
2 2^21 2^21*0 2^21*1 2^21*2 。。。。。。。 2^21*19 2^21*20 2^21*21
3 3^21 3^21*0 3^21*1 3^21*2 。。。。。。。 3^21*19 3^21*20 3^21*21
4 4^21 4^21*0 4^21*1 4^21*2 。。。。。。。 4^21*19 4^21*20 4^21*21
5 5^21 5^21*0 5^21*1 5^21*2 。。。。。。。 5^21*19 5^21*20 5^21*21
6 6^21 6^21*0 6^21*1 6^21*2 。。。。。。。 6^21*19 6^21*20 6^21*21
7 7^21 7^21*0 7^21*1 7^21*2 。。。。。。。 7^21*19 7^21*20 7^21*21
8 8^21 8^21*0 8^21*1 8^21*2 。。。。。。。 8^21*19 8^21*20 8^21*21
9 9^21 9^21*0 9^21*1 9^21*2 。。。。。。。 9^21*19 9^21*20 9^21*21
剪枝:
9^21是一个21位数,9^21*10是一个22位数(超过21),即9^21最多出现9次,因此9只需从0~9次枚举其出现次数,而0不能做数字开头,0从0~20次枚举,其他数字从0~21次枚举。需要注意的是,在10层的多重枚举循环中, CPU切换循环层时也需要时间,所以一般来说将次数少的循环放在外层,将循环次数多的放在内层。故十重循环中将9放在最外层,然后是0 、1,然后是剩余的。
其他位的水仙花也可采用一样的做法,只需改变valus[i][j][k]存储的内容 及 数字出现的次数 即可。
#include
#include
using namespace std;
//value[i][j][k]为数字i的21次方出现j次的值(即i^21 * j),其中k为该值的长度
char value[10][22][22]={"000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000","000000000000000000000",
"000000000000000000000","000000000000000000001","000000000000000000002","000000000000000000003","000000000000000000004","000000000000000000005","000000000000000000006","000000000000000000007","000000000000000000008","000000000000000000009","000000000000000000010","000000000000000000011","000000000000000000012","000000000000000000013","000000000000000000014","000000000000000000015","000000000000000000016","000000000000000000017","000000000000000000018","000000000000000000019","000000000000000000020","000000000000000000021",
"000000000000000000000","000000000000002097152","000000000000004194304","000000000000006291456","000000000000008388608","000000000000010485760","000000000000012582912","000000000000014680064","000000000000016777216","000000000000018874368","000000000000020971520","000000000000023068672","000000000000025165824","000000000000027262976","000000000000029360128","000000000000031457280","000000000000033554432","000000000000035651584","000000000000037748736","000000000000039845888","000000000000041943040","000000000000044040192",
"000000000000000000000","000000000010460353203","000000000020920706406","000000000031381059609","000000000041841412812","000000000052301766015","000000000062762119218","000000000073222472421","000000000083682825624","000000000094143178827","000000000104603532030","000000000115063885233","000000000125524238436","000000000135984591639","000000000146444944842","000000000156905298045","000000000167365651248","000000000177826004451","000000000188286357654","000000000198746710857","000000000209207064060","000000000219667417263",
"000000000000000000000","000000004398046511104","000000008796093022208","000000013194139533312","000000017592186044416","000000021990232555520","000000026388279066624","000000030786325577728","000000035184372088832","000000039582418599936","000000043980465111040","000000048378511622144","000000052776558133248","000000057174604644352","000000061572651155456","000000065970697666560","000000070368744177664","000000074766790688768","000000079164837199872","000000083562883710976","000000087960930222080","000000092358976733184",
"000000000000000000000","000000476837158203125","000000953674316406250","000001430511474609375","000001907348632812500","000002384185791015625","000002861022949218750","000003337860107421875","000003814697265625000","000004291534423828125","000004768371582031250","000005245208740234375","000005722045898437500","000006198883056640625","000006675720214843750","000007152557373046875","000007629394531250000","000008106231689453125","000008583068847656250","000009059906005859375","000009536743164062500","000010013580322265625",
"000000000000000000000","000021936950640377856","000043873901280755712","000065810851921133568","000087747802561511424","000109684753201889280","000131621703842267136","000153558654482644992","000175495605123022848","000197432555763400704","000219369506403778560","000241306457044156416","000263243407684534272","000285180358324912128","000307117308965289984","000329054259605667840","000350991210246045696","000372928160886423552","000394865111526801408","000416802062167179264","000438739012807557120","000460675963447934976",
"000000000000000000000","000558545864083284007","001117091728166568014","001675637592249852021","002234183456333136028","002792729320416420035","003351275184499704042","003909821048582988049","004468366912666272056","005026912776749556063","005585458640832840070","006144004504916124077","006702550368999408084","007261096233082692091","007819642097165976098","008378187961249260105","008936733825332544112","009495279689415828119","010053825553499112126","010612371417582396133","011170917281665680140","011729463145748964147",
"000000000000000000000","009223372036854775808","018446744073709551616","027670116110564327424","036893488147419103232","046116860184273879040","055340232221128654848","064563604257983430656","073786976294838206464","083010348331692982272","092233720368547758080","101457092405402533888","110680464442257309696","119903836479112085504","129127208515966861312","138350580552821637120","147573952589676412928","156797324626531188736","166020696663385964544","175244068700240740352","184467440737095516160","193690812773950291968",
"000000000000000000000","109418989131512359209","218837978263024718418","328256967394537077627","437675956526049436836","547094945657561796045","656513934789074155254","765932923920586514463","875351913052098873672","984770902183611232881"};
/*10个大数求和*/
void add(char* A0,char* A1,char* A2,char* A3,char* A4,char* A5,char* A6,char* A7,char* A8,char* A9,char* ans)
{
int a0[22]={0},a1[22]={0},a2[22]={0},a3[22]={0},a4[22]={0},a5[22]={0},a6[22]={0},a7[22]={0},a8[22]={0},a9[22]={0};
int p=20;
/*倒序 & 转换*/
for(int q=0;q<=20;q++,p--)
{
a0[q]=A0[p]-'0';
a1[q]=A1[p]-'0';
a2[q]=A2[p]-'0';
a3[q]=A3[p]-'0';
a4[q]=A4[p]-'0';
a5[q]=A5[p]-'0';
a6[q]=A6[p]-'0';
a7[q]=A7[p]-'0';
a8[q]=A8[p]-'0';
a9[q]=A9[p]-'0';
}
int w=0; //低位到高位的进位
char* b=new char[22];
for(p=0;p<=20;p++)
{
int temp=a0[p]+a1[p]+a2[p]+a3[p]+a4[p]+a5[p]+a6[p]+a7[p]+a8[p]+a9[p]+w;
b[p]=temp%10+'0';
w=temp/10;
}
if(w!=0) //说明ans有22位,不符合
{
ans[0]='0';
ans[1]='\0';
return;
}
for(p=20;w<=20;w++)
ans[w]=b[p--]; //ans可能不足21位
ans[w]='\0';
return;
}
/*判断ans内各个数字出现的次数 是否与 枚举各个数字时每个数字出现的次数分别相同*/
bool judge(int i0,int i1,int i2,int i3,int i4,int i5,int i6,int i7,int i8,int i9,char* ans)
{
int time[10]={0}; //ans各个数字出现的次数
for(int i=0;i<=20;i++)
time[ ans[i]-'0' ]++;
if(time[0]==i0 && time[1]==i1 && time[2]==i2 && time[3]==i3 && time[4]==i4 &&
time[5]==i5 && time[6]==i6 && time[7]==i7 && time[8]==i8 && time[9]==i9)
return true;
return false;
}
int main(void)
{
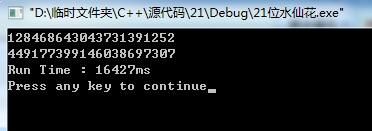
int time=GetTickCount();
char ans[22];
/*枚举数字0~9出现的次数*/
for(int i9=0;i9<=9;i9++)
{
for(int i0=0;i0<=20;i0++)
{
if(i0+i9==21)
{
add(value[0][i0],value[1][0],value[2][0],value[3][0],value[4][0],value[5][0],value[6][0],value[7][0],value[8][0],value[9][i9],ans);
if(ans[0]!='0' && judge(i0,0,0,0,0,0,0,0,0,i9,ans)) //ans[0]!='0'保证ans为21位
cout<