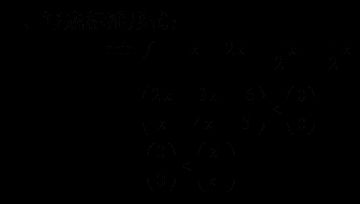MatLab的优化工具箱很不错,记得以前用的版本都是通过命令操作,但是在10版本中似乎有一个可视化的界面,不过命令我忘记了,悲哀。Matlab提供的功能主要有线性规划、非线性规划、极值问题等,这些也是比较常见的优化问题。
优化工具箱概述
1.MATLAB求解优化问题的主要函数
2.优化函数的输入变量
使用优化函数或优化工具箱中其它优化函数时, 输入变量见下表:
3. 优化函数的输出变量下表:
4.控制参数options的设置
Options中常用的几个参数的名称、含义、取值如下:
(1) Display: 显示水平.取值为’off’时,不显示输出; 取值为’iter’时,显示每次迭代的信息;取值为’final’时,显示最终结果.默认值为’final’.
(2) MaxFunEvals: 允许进行函数评价的最大次数,取值为正整数.
(3) MaxIter: 允许进行迭代的最大次数,取值为正整数
控制参数options可以通过函数optimset创建或修改。命令的格式如下:
(1) options=optimset(‘optimfun’)
创建一个含有所有参数名,并与优化函数optimfun相关的默认值的选项结构options.
(2)options=optimset(‘param1’,value1,’param2’,value2,...)
创建一个名称为options的优化选项参数,其中指定的参数具有指定值,所有未指定的参数取默认值.
(3)options=optimset(oldops,‘param1’,value1,’param2’,
value2,...)
创建名称为oldops的参数的拷贝,用指定的参数值修改oldops中相应的参数.
例:opts=optimset(‘Display’,’iter’,’TolFun’,1e-8)
该语句创建一个称为opts的优化选项结构,其中显示参数设为’iter’, TolFun参数设为1e-8.
用Matlab解无约束优化问题
一元函数无约束优化问题![]()
常用格式如下:
(1)x= fminbnd (fun,x1,x2)
(2)x= fminbnd (fun,x1,x2 ,options)
(3)[x,fval]= fminbnd(...)
(4)[x,fval,exitflag]= fminbnd(...)
(5)[x,fval,exitflag,output]= fminbnd(...)
其中(3)、(4)、(5)的等式右边可选用(1)或(2)的等式右边。
函数fminbnd的算法基于黄金分割法和二次插值法,它要求目标函数必须是连续函数,并可能只给出局部最优解。
例1 求![]() 在0
在0
主程序为wliti1.m:
f='2*exp(-x).*sin(x)';
fplot(f,[0,8]); %作图语句
[xmin,ymin]=fminbnd (f, 0,8)
f1='-2*exp(-x).*sin(x)';
[xmax,ymax]=fminbnd (f1, 0,8)
运行结果:
xmin = 3.9270 ymin = -0.0279
xmax = 0.7854 ymax = 0.6448
例2 对边长为3米的正方形铁板,在四个角剪去相等的正方形以制成方形无盖水槽,问如何剪法使水槽的容积最大?
先编写M文件fun0.m如下:
function f=fun0(x)
f=-(3-2*x).^2*x;
主程序为wliti2.m:
[x,fval]=fminbnd('fun0',0,1.5);
xmax=x
fmax=-fval
运算结果为: xmax = 0.5000,fmax =2.0000.即剪掉的正方形的边长为0.5米时水槽的容积最大,最大容积为2立方米.
2、多元函数无约束优化问题
标准型为:min F(X)
命令格式为:
(1)x= fminunc(fun,X0 );或x=fminsearch(fun,X0 )
(2)x= fminunc(fun,X0 ,options);
或x=fminsearch(fun,X0 ,options)
(3)[x,fval]= fminunc(...);
或[x,fval]= fminsearch(...)
(4)[x,fval,exitflag]= fminunc(...);
或[x,fval,exitflag]= fminsearch
(5)[x,fval,exitflag,output]= fminunc(...);
或[x,fval,exitflag,output]= fminsearch(...)
说明:
• fminsearch是用单纯形法寻优. fminunc的算法见以下几点说明:
[1] fminunc为无约束优化提供了大型优化和中型优化算法。由options中的参数LargeScale控制:
LargeScale=’on’(默认值),使用大型算法
LargeScale=’off’(默认值),使用中型算法
[2] fminunc为中型优化算法的搜索方向提供了4种算法,由
options中的参数HessUpdate控制:
HessUpdate=’bfgs’(默认值),拟牛顿法的BFGS公式;
HessUpdate=’dfp’,拟牛顿法的DFP公式;
HessUpdate=’steepdesc’,最速下降法
[3] fminunc为中型优化算法的步长一维搜索提供了两种算法, 由options中参数LineSearchType控制:
LineSearchType=’quadcubic’(缺省值),混合的二次和三次多项式插值;
LineSearchType=’cubicpoly’,三次多项式插
• 使用fminunc和 fminsearch可能会得到局部最优解.
例3 min f(x)=(4x12+2x22+4x1x2+2x2+1)*exp(x1)
1、编写M-文件 fun1.m:
function f = fun1 (x)
f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
2、输入M文件wliti3.m如下:
x0 = [-1, 1];
x=fminunc(‘fun1’,x0);
y=fun1(x)
3、运行结果:
x= 0.5000 -1.0000
y = 1.3029e-10
例4 Rosenbrock 函数 f(x1,x2)=100(x2-x12)2+(1-x1)2
的最优解(极小)为x*=(1,1),极小值为f*=0.试用
不同算法(搜索方向和步长搜索)求数值最优解.
初值选为x0=(-1.2 , 2).
1.为获得直观认识,先画出Rosenbrock 函数的三维图形,
输入以下命令:
[x,y]=meshgrid(-2:0.1:2,-1:0.1:3);
z=100*(y-x.^2).^2+(1-x).^2;
mesh(x,y,z)
2. 画出Rosenbrock 函数的等高线图,输入命令:
contour(x,y,z,20)
hold on
plot(-1.2,2,' o ');
text(-1.2,2,'start point')
plot(1,1,'o')
text(1,1,'solution')
3.用fminsearch函数求解
输入命令:
f='100*(x(2)-x(1)^2)^2+(1-x(1))^2';
[x,fval,exitflag,output]=fminsearch(f, [-1.2 2])
运行结果:
x =1.0000 1.0000
fval =1.9151e-010
exitflag = 1
output =
iterations: 108
funcCount: 202
algorithm: 'Nelder-Mead simplex direct search'
4. 用fminunc 函数
(1)建立M-文件fun2.m
function f=fun2(x)
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2
(2)主程序wliti44.m
Rosenbrock函数不同算法的计算结果
可以看出,最速下降法的结果最差.因为最速下降法特别不适合于从一狭长通道到达最优解的情况.
例5 产销量的最佳安排
某厂生产一种产品有甲、乙两个牌号,讨论在产销平衡的情况下如何确定各自的产量,使总利润最大. 所谓产销平衡指工厂的产量等于市场上的销量.
符号说明
z(x1,x2)表示总利润;
p1,q1,x1分别表示甲的价格、成本、销量;
p2,q2,x2分别表示乙的价格、成本、销量;
aij,bi,λi,ci(i,j =1,2)是待定系数.
基本假设
1.价格与销量成线性关系
利润既取决于销量和价格,也依赖于产量和成本。按照市场规律,
甲的价格p1会随其销量x1的增长而降低,同时乙的销量x2的增长也
会使甲的价格有稍微的下降,可以简单地假设价格与销量成线性关系,
即: p1 = b1 - a11 x1 - a12 x2 ,b1,a11,a12> 0,且a11 > a12;
同理, p2 = b2 - a21 x1- a22 x2 ,b2,a21,a22 > 0
2.成本与产量成负指数关系
甲的成本随其产量的增长而降低,且有一个渐进值,可以假设为
负指数关系,即:
![]()
![]()
同理, ![]()
![]()
模型建立
总利润为: z(x1,x2)=(p1-q1)x1+(p2-q2)x2
若根据大量的统计数据,求出系数b1=100,a11=1,a12=0.1,b2=280,
a21=0.2,a22=2,r1=30,λ1=0.015,c1=20, r2=100,λ2=0.02,c2=30,则
问题转化为无约束优化问题:求甲,乙两个牌号的产量x1,x2,使
总利润z最大.
为简化模型,先忽略成本,并令a12=0,a21=0,问题转化为求:
z1 = ( b1 - a11x1 ) x1 + ( b2 - a22x2 ) x2
的极值. 显然其解为x1 = b1/2a11 = 50, x2 = b2/2a22 = 70,
我们把它作为原问题的初始值.
模型求解
1.建立M-文件fun.m:
function f = fun(x)
y1=((100-x(1)- 0.1*x(2))-(30*exp(-0.015*x(1))+20))*x(1);
y2=((280-0.2*x(1)- 2*x(2))-(100*exp(-0.02*x(2))+30))*x(2);
f=-y1-y2;
2.输入命令:
x0=[50,70];
x=fminunc(‘fun’,x0),
z=fun(x)
3.计算结果:
x=23.9025, 62.4977, z=6.4135e+003
即甲的产量为23.9025,乙的产量为62.4977,最大利润为6413.5.
二次规划
 |
用MATLAB软件求解,其输入格式如下:
1. x=quadprog(H,C,A,b);
2. x=quadprog(H,C,A,b,Aeq,beq);
3. x=quadprog(H,C,A,b,Aeq,beq,VLB,VUB);
4. x=quadprog(H,C,A,b, Aeq,beq ,VLB,VUB,X0);
5. x=quadprog(H,C,A,b, Aeq,beq ,VLB,VUB,X0,options);
6. [x,fval]=quaprog(...);
7. [x,fval,exitflag]=quaprog(...);
8. [x,fval,exitflag,output]=quaprog(...);
例1 min f(x1,x2)=-2x1-6x2+x12-2x1x2+2x22
s.t. x1+x2≤2
-x1+2x2≤2
x1≥0, x2≥0
1、写成标准形式:
2、 输入命令:
H=[1 -1; -1 2];
c=[-2 ;-6];A=[1 1; -1 2];b=[2;2];
Aeq=[];beq=[]; VLB=[0;0];VUB=[];
[x,z]=quadprog(H,c,A,b,Aeq,beq,VLB,VUB)
3、运算结果为:
x =0.6667 1.3333 z = -8.2222
一般非线性规划
标准型为:
min F(X)
s.t AX<=b ![]() G(X)
G(X)![]()
Ceq(X)=0 VLB![]() X
X![]() VUB
VUB
其中X为n维变元向量,G(X)与Ceq(X)均为非线性函数组成的向量,其它变量的含义与线性规划、二次规划中相同.用Matlab求解上述问题,基本步骤分三步:
1. 首先建立M文件fun.m,定义目标函数F(X):
function f=fun(X);
f=F(X);
2. 若约束条件中有非线性约束:G(X)![]() 或Ceq(X)=0,则建立M文件nonlcon.m定义函数G(X)与Ceq(X):
或Ceq(X)=0,则建立M文件nonlcon.m定义函数G(X)与Ceq(X):
function [G,Ceq]=nonlcon(X)
G=...
Ceq=...
3. 建立主程序.非线性规划求解的函数是fmincon,命令的基本格式如下:
(1) x=fmincon(‘fun’,X0,A,b)
(2) x=fmincon(‘fun’,X0,A,b,Aeq,beq)
(3) x=fmincon(‘fun’,X0,A,b, Aeq,beq,VLB,VUB)
(4) x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’)
(5)x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’,options)
(6) [x,fval]= fmincon(...)
(7) [x,fval,exitflag]= fmincon(...)
(8)[x,fval,exitflag,output]= fmincon(...)
注意:
[1] fmincon函数提供了大型优化算法和中型优化算法。默认时,若在fun函数中提供了梯度(options参数的GradObj设置为’on’),并且只有上下界存在或只有等式约束,fmincon函数将选择大型算法。当既有等式约束又有梯度约束时,使用中型算法。
[2] fmincon函数的中型算法使用的是序列二次规划法。在每一步迭代中求解二次规划子问题,并用BFGS法更新拉格朗日Hessian矩阵。
[3] fmincon函数可能会给出局部最优解,这与初值X0的选取有关。
2、先建立M-文件 fun3.m:
function f=fun3(x);
f=-x(1)-2*x(2)+(1/2)*x(1)^2+(1/2)*x(2)^2
3、再建立主程序youh2.m:
x0=[1;1];
A=[2 3 ;1 4]; b=[6;5];
Aeq=[];beq=[];
VLB=[0;0]; VUB=[];
[x,fval]=fmincon('fun3',x0,A,b,Aeq,beq,VLB,VUB)
4、运算结果为:
x = 0.7647 1.0588
fval = -2.0294
例3
1.先建立M文件 fun4.m,定义目标函数:
function f=fun4(x);
f=exp(x(1))
*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
2.再建立M文件mycon.m定义非线性约束:
function [g,ceq]=mycon(x)
g=[x(1)+x(2);1.5+x(1)*x(2)-x(1)-x(2);-x(1)*x(2)-10];
3.主程序youh3.m为:
x0=[-1;1];
A=[];b=[];
Aeq=[1 1];beq=[0];
vlb=[];vub=[];
[x,fval]=fmincon('fun4',x0,A,b,Aeq,beq,vlb,vub,'mycon')
3. 运算结果为:
x = -1.2250 1.2250
fval = 1.8951
例4.资金使用问题
设有400万元资金, 要求4年内使用完, 若在一年内使用资金x万元, 则可得效益![]() 万元(效益不能再使用),当年不用的资金可存入银行, 年利率为10%. 试制定出资金的使用计划, 以使4年效益之和为最大.
万元(效益不能再使用),当年不用的资金可存入银行, 年利率为10%. 试制定出资金的使用计划, 以使4年效益之和为最大.
设变量![]() 表示第i年所使用的资金数,则有
表示第i年所使用的资金数,则有
1.先建立M文件 fun44.m,定义目标函数:
function f=fun44(x)
f=-(sqrt(x(1))+sqrt(x(2))+sqrt(x(3))+sqrt(x(4)));
2.再建立M文件mycon1.m定义非线性约束:
function [g,ceq]=mycon1(x)
g(1)=x(1)-400;
g(2)=1.1*x(1)+x(2)-440;
g(3)=1.21*x(1)+1.1*x(2)+x(3)-484;
g(4)=1.331*x(1)+1.21*x(2)+1.1*x(3)+x(4)-532.4;
ceq=0
3.主程序youh4.m为:
x0=[1;1;1;1];vlb=[0;0;0;0];vub=[];A=[];b=[];Aeq=[];beq=[];
[x,fval]=fmincon('fun44',x0,A,b,Aeq,beq,vlb,vub,'mycon1')
线性规划问题
线性规划问题是目标函数和约束条件均为线性函数的问题,MATLAB6.0 解决的线性规划问题的标准形式为:
min f(x)
sub.to:
x A ≤b ⋅ x Aeq = beq⋅ ub≤ x≤ lb
其中 f、x、b、beq、lb、ub 为向量,A、Aeq 为矩阵。 其它形式的线性规划问题都可经过适当变换化为此标准形式。
x = linprog(f,A,b,Aeq,beq,lb,ub,x0) %设置初值 x0
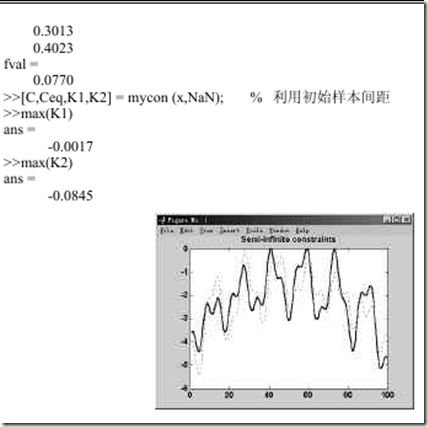
“半无限”有约束的多元函数最优解
x = fseminf(fun,x0,ntheta,seminfcon)
x = fseminf(fun,x0,ntheta,seminfcon,A,b)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub)
x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub,options)
[x,fval] = fseminf(⋯)
[x,fval,exitflag] = fseminf(⋯)
[x,fval,exitflag,output] = fseminf(⋯)
[x,fval,exitflag,output,lambda] = fseminf(⋯)
极小化极大问题
例子:
最小二乘最优问题
约束线性最小二乘
非线性数据拟合
非线性最小二乘
非负线性最小二乘
非线性方程的解
非线性方程的标准形式为 f(x)=0
函数 fzero
格式 x = fzero (fun,x0) %用 fun 定义表达式 f(x),x0 为初始解。
x = fzero (fun,x0,options)
[x,fval] = fzero(⋯) %fval=f(x)
[x,fval,exitflag] = fzero(⋯)
[x,fval,exitflag,output] = fzero(⋯)
说明 该函数采用数值解求方程 f(x)=0 的根。
非线性方程组的解
非线性方程组的标准形式为:F(x) = 0
其中:x 为向量,F(x)为函数向量。
函数 fsolve
格式 x = fsolve(fun,x0) %用 fun 定义向量函数,其定义方式为:先定义方程函数
function F = myfun (x)。
F =[表达式 1;表达式 2;⋯表达式 m] %保存为 myfun.m,并用下面方式调用:
x = fsolve(@myfun,x0),x0 为初始估计值。
x = fsolve(fun,x0,options)
[x,fval] = fsolve(⋯) %fval=F(x),即函数值向量
[x,fval,exitflag] = fsolve(⋯)
[x,fval,exitflag,output] = fsolve(⋯)
[x,fval,exitflag,output,jacobian] = fsolve(⋯) % jacobian 为解 x 处的 Jacobian 阵。
http://www.cnblogs.com/feisky/archive/2009/10/24/1589260.html