1 分布分析
1.1 定义
分布分析 ：研究数据的分布特征和分布类型，分定量数据、定性数据区分基本统计量
定量数据：了解其分布形式，对称或者非对称，发现某些特大或特小的异常值,可通过绘制散点图，频率分布直方图，茎叶图直观的分析
定性数据：可用饼图或和条形图直观的显示分布情况
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 数据读取
data = pd.read_csv('C:/Users/Hjx/Desktop/深圳罗湖二手房信息.csv',engine = 'python')
data.head()#查看数据
通过数据可见，一共8个字段
定量字段：房屋单价，参考首付，参考总价， 经度，纬度，*房屋编码
定性字段：小区，朝向
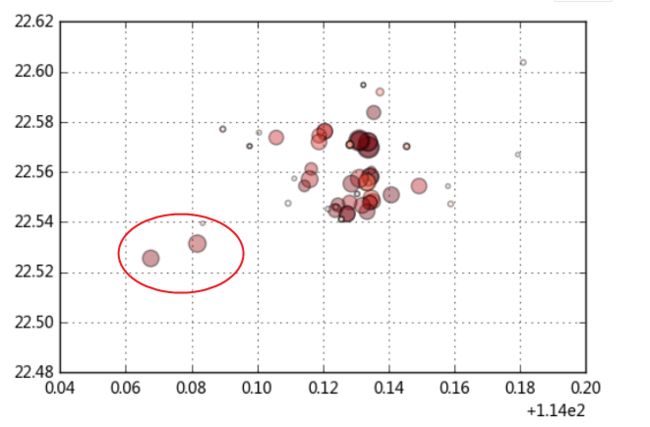
plt.scatter(data['经度'],data['纬度'], # 按照经纬度显示
s = data['房屋单价']/500, # 按照单价显示大小
c = data['参考总价'], # 按照总价显示颜色
alpha = 0.4, cmap = 'Reds')
plt.grid()
根据经纬度绘制散点图，查看异常值
红圈内两处住宅房屋单价较高，且离中心城区较远，可能为郊区豪宅
1.2 定量数据的分布分析
选择‘组数’和‘组宽’是做频率分布分析时最主要的问题，一般按照如下步骤进行
1）求极差
def d_range(df,*cols):
krange = []
for col in cols:
crange = df[col].max() - df[col].min()
krange.append(crange)
return(krange)
# 创建函数求极差
key1 = '参考首付'
key2 = '参考总价'
dr = d_range(data,key1,key2)
print('%s极差为 %f \n%s极差为 %f' % (key1, dr[0], key2, dr[1]))
参考首付极差为 52.500000
参考总价极差为 175.000000
2）决定‘组数’和‘组宽’
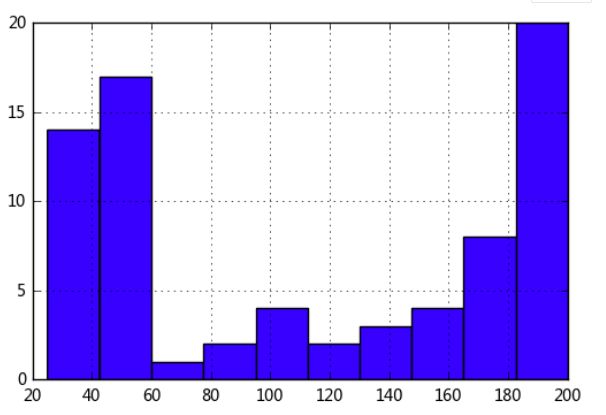
通过直方图直接判断分组组数
data[key2].hist(bins=10)
# 简单查看数据分布，确定分布组数 → 一般8-16即可
# 这里以10组为参考
3）决定分点
gcut = pd.cut(data['参考总价'],10,right = False)#等宽分成10组
data['参考总价分组'] = gcut.values
gcut.value_counts(sort = False)
分布区间表
4）列出频率分布表
r_zj = pd.DataFrame(gcut.value_counts())
r_zj.columns = ['频数']
r_zj['频率'] = r_zj / r_zj['频数'].sum() # 计算频率
r_zj['累计频率'] = r_zj['频率'].cumsum() # 计算累计频率
r_zj['频率%'] = r_zj['频率'].map(lambda x: "%.2f%%" % (x*100)) # 以百分比显示频率
r_zj['累计频率%'] = r_zj['累计频率'].map(lambda x: "%.2f%%" % (x*100)) # 以百分比显示累计频率
频率分布表
5）绘制频率分布直方图
r_zj['频率'].plot(kind = 'bar',
width = 0.8,
figsize = (12,2),
rot = 0,
color = 'k',
grid = True,
alpha = 0.5)
plt.title('参考总价分布频率直方图')
# 绘制直方图
x = len(r_zj)
y = r_zj['频率']
m = r_zj['频数']
for i,j,k in zip(range(x),y,m):
plt.text(i-0.1,j+0.01,'%i' % k, color = 'k')
# 添加频数标签
参考总价频率分布图
1.3定性数据的分布分析
根据变量的分类类型来分组，可以采用饼图和条形图来描述定性变量的分布
cx_g = data['朝向'].value_counts(sort=True)
# 统计频率
r_cx = pd.DataFrame(cx_g)
r_cx.rename(columns ={cx_g.name:'频数'}, inplace = True) # 修改频数字段名
r_cx['频率'] = r_cx / r_cx['频数'].sum() # 计算频率
r_cx['累计频率'] = r_cx['频率'].cumsum() # 计算累计频率
r_cx['频率%'] = r_cx['频率'].apply(lambda x: "%.2f%%" % (x*100)) # 以百分比显示频率
r_cx['累计频率%'] = r_cx['累计频率'].apply(lambda x: "%.2f%%" % (x*100)) # 以百分比显示累计频率
r_cx.style.bar(subset=['频率','累计频率'], color='#d65f5f',width=100)
频率分布图
plt.figure(num = 1,figsize = (12,2))
r_cx['频率'].plot(kind = 'bar',
width = 0.8,
rot = 0,
color = 'k',
grid = True,
alpha = 0.5,
figsize = (12,2))
# 绘制直方图
朝向频率直方图
直方图的高度代表每一类型的百分比或频数，条形图的宽度没有意义
plt.figure(num = 2)
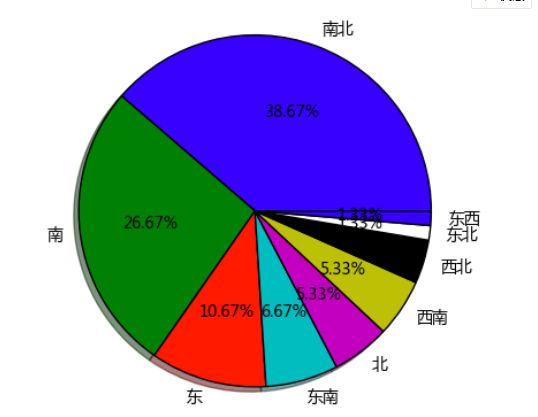
plt.pie(r_cx['频数'],
labels = r_cx.index,
autopct='%.2f%%',
shadow = True)
plt.axis('equal')
# 绘制饼图
朝向分布饼图
饼图的每一个扇形部分代表每一个类型的百分比或者频数
2 对比分析
2.1 定义
两个互相联系的指标进行比较，特别适用于指标间的纵横向比较，时间序列的比较分析
2.2 绝对数比较
利用绝对数进行对比，从而寻找差异的一种方法
data = pd.DataFrame(np.random.rand(30,2)*1000,
columns = ['A_sale','B_sale'],
index = pd.period_range('20170601','20170630'))
print(data.head())
# 创建数据
30天内A/B产品的日销售额
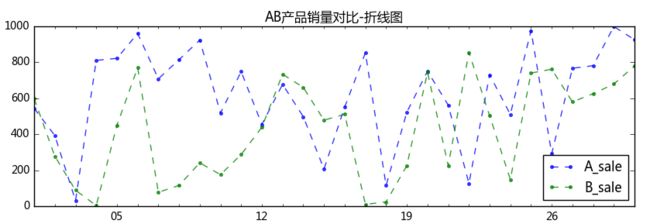
data.plot(kind='line',
style = '--.',
alpha = 0.8,
figsize = (10,3),
title = 'AB产品销量对比-折线图')
# 折线图比较
折线图比较
data.plot(kind = 'bar',
width = 0.8,
alpha = 0.8,
figsize = (10,3),
title = 'AB产品销量对比-柱状图')
# 柱状图比较
image.png
2.3 相对数比较
由连个有联系的指标对比计算，反映客观现象之间数量联系程度的综合指标，其数值表现为相对数
2.2.1 结构相对数
将同一总体内的部分数值与全部数值对比，求的比重，用以说明事物的性质，结构或者质量。如居民食品支出额占消费支出总额比重，销售额占比，完成率
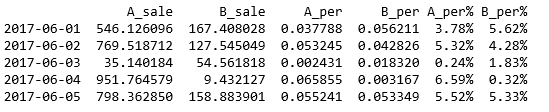
data = pd.DataFrame({'A_sale':np.random.rand(30)*1000,
'B_sale':np.random.rand(30)*200},
index = pd.period_range('20170601','20170630'))
# 创建数据 → 30天内A/B产品的日销售额
data['A_per'] = data['A_sale'] / data['A_sale'].sum()
data['B_per'] = data['B_sale'] / data['B_sale'].sum()
# 计算出每天的营收占比
data['A_per%'] = data['A_per'].apply(lambda x: '%.2f%%' % (x*100))
data['B_per%'] = data['B_per'].apply(lambda x: '%.2f%%' % (x*100))
# 转换为百分数
30天内A/B产品的日销售额占比
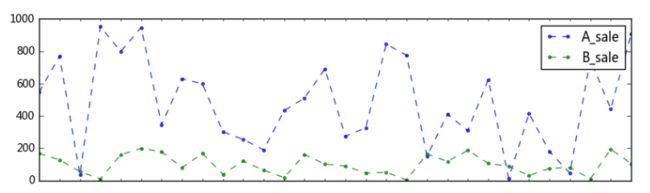
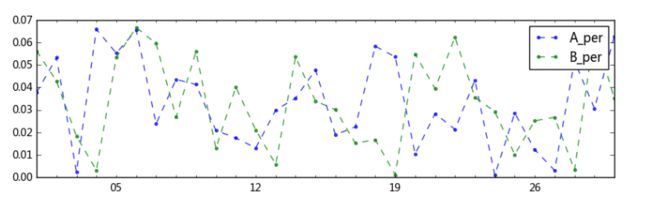
fig,axes = plt.subplots(2,1,figsize = (10,6),sharex=True)
data[['A_sale','B_sale']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[0])
axes[0].legend(loc = 'upper right')
data[['A_per','B_per']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[1])
axes[1].legend(loc = 'upper right')
# 绝对值对比较难看出结构性变化，通过看销售额占比来看售卖情况的对比
绝对数对比
结构相对数对比
2.2.2 比例相对数
将同一总体内不同部分的数值进行比较，表明总体内各部分的比例关系，如人口性别比列，投资与消费比例，基本建设投资额中工业、农业、教育投资的比例
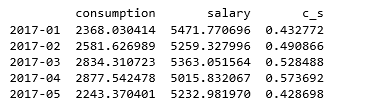
data = pd.DataFrame({'consumption':np.random.rand(12)*1000 + 2000,
'salary':np.random.rand(12)*500 + 5000},
index = pd.period_range('2017/1','2017/12',freq = 'M'))
# 创建数据 → 某人一年内的消费、工资薪水情况
# 消费按照2000-3000/月随机，工资按照5000-5500/月随机
data['c_s'] = data['consumption'] / data['salary']
print(data.head())
# 比例相对数 → 消费收入比
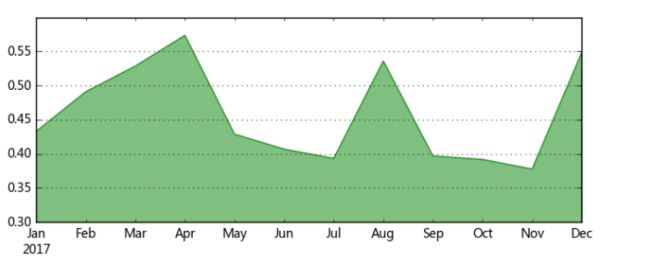
data['c_s'].plot.area(color = 'green',alpha = 0.5,ylim = [0.3,0.6],figsize=(8,3),grid=True)
# 创建面积图表达
某人一年内的消费、工资薪水情况
比例相对数面积图
2.2.3 比较相对数
将同一时期两个性质相同的指标数值经行对比，说明同类现象在不同空间条件下的数量关系对比，如不同地区商品价格对比，不同行业，不同企业间某项指标的对比
data = pd.DataFrame({'A':np.random.rand(30)*5000,
'B':np.random.rand(30)*2000,
'C':np.random.rand(30)*10000,
'D':np.random.rand(30)*800},
index = pd.period_range('20170601','20170630'))
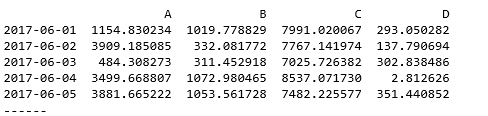
print(data.head())
print('------')
# 创建数据 → 30天内A/B/C/D四个产品的销售情况
30天内A/B/C/D四个产品的销售情况
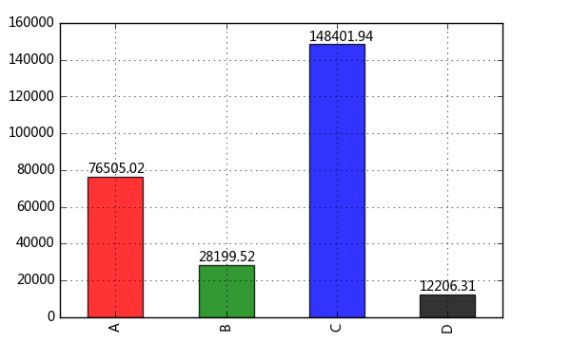
data.sum().plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True)
for i,j in zip(range(4),data.sum()):
plt.text(i-0.25,j+2000,'%.2f' % j, color = 'k')
# 通过柱状图做横向比较 → 4个产品的销售额总量
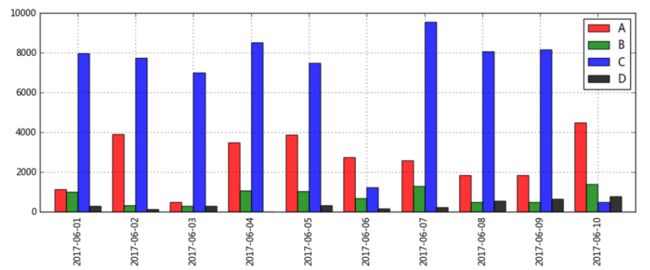
data[:10].plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True,
figsize = (12,4),width = 0.8)
# 多系列柱状图，横向比较前十天4个产品的销售额
4个产品的销售额总量
前十天4个产品的销售额
关于同比与环比
同比:产品A在2015.3和2016.3的比较（相邻时间段的同一时间点）
环比:产品A在2015.3和2015.4的比较（相邻时间段的比较）
如何界定“相邻时间段”与“时间点”，决定了是同比还是环比
2.2.4 动态相对数
将同一现象在不同时期的指标数值进行对比，用以说明发展方向和变化的速度。如发展速度，增长速度等
基本方法:计算动态相对数即发展速度
动态相对数（发展速度） = 某一现象的报告期数值 / 同一现象的基期数值
基期：用来比较的基础时期
报告期：所要研究的时期，又称计算期
data = pd.DataFrame({'A':np.random.rand(30)*2000+1000},
index = pd.period_range('20170601','20170630'))
print(data.head())
print('------')
# 创建数据 → 30天内A产品的销售情况
data['base'] = 1000 # 假设基期销售额为1000，后面每一天都为计算期
data['l_growth'] = data['A'] - data['base'] # 累计增长量 = 报告期水平 - 固定基期水平
data['z_growth'] = data['A'] - data.shift(1)['A'] # 逐期增长量 = 报告期水平 - 报告期前一期水平
data = data.fillna(0) # 替换缺失值
data['lspeed'] = data['l_growth'] / 1000 # 定基增长速度
data['zspeed'] = data['z_growth'] / data.shift(1)['A'] # 环比增长速度
增长量情况
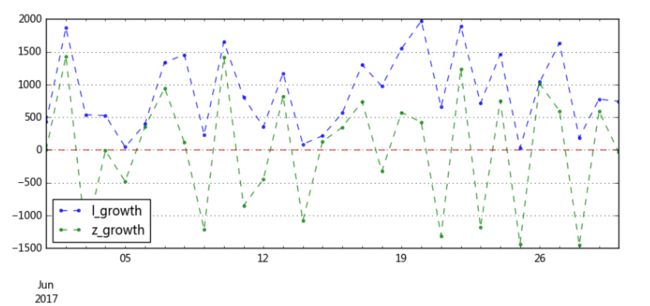
data[['l_growth','z_growth']].plot(figsize = (10,4),style = '--.',alpha = 0.8)
plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线
plt.legend(loc = 'lower left')
plt.grid()
# 通过折线图查看增长量情况
A产品增长量情况
根据增长量图示A产品缓慢增长，平稳发展，未出现大幅下降。
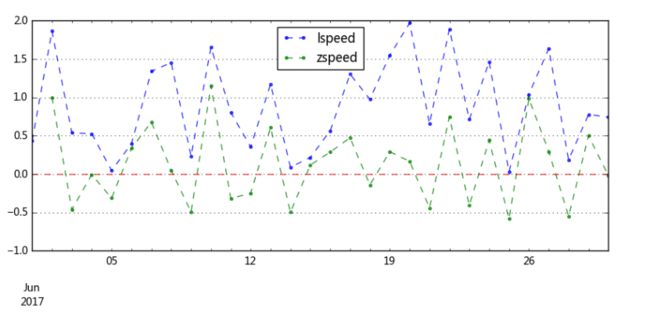
data['lspeed'] = data['l_growth'] / 1000 # 定基增长速度
data['zspeed'] = data['z_growth'] / data.shift(1)['A'] # 环比增长速度
data[['lspeed','zspeed']].plot(figsize = (10,4),style = '--.',alpha = 0.8)
plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线
plt.grid()
A产品发展速度情况