wikipedia上的解释和证明:http://en.wikipedia.org/wiki/Tonelli%E2%80%93Shanks_algorithm
The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used within modular arithmetic to solve a congruence of the form
where n is a quadratic residue (mod p), and p is an odd prime.
Tonelli–Shanks cannot be used for composite moduli; finding square roots modulo composite numbers is a computational problem equivalent to integer factorization.[1]
An equivalent, but slightly more redundant version of this algorithm was developed by Alberto Tonelli in 1891. The version discussed here was developed independently by Daniel Shanksin 1973, who explained:
"My tardiness in learning of these historical references was because I had lent Volume 1 of Dickson's History to a friend and it was never returned."[2]
(Note: All  are taken to mean
are taken to mean 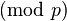 , unless indicated otherwise).[edit]The algorithm
, unless indicated otherwise).[edit]The algorithm
Inputs: p, an odd prime. n, an integer which is a quadratic residue (mod p), meaning that the Legendre symbol ![]() .
.
Outputs: R, an integer satisfying ![]() .
.
- Factor out powers of 2 from p − 1, defining Q and S as:
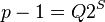 with Q odd. Note that if
with Q odd. Note that if 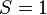 , i.e.
, i.e. 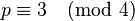 , then solutions are given directly by
, then solutions are given directly by 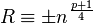 .
. - Select a z such that the Legendre symbol
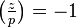 (that is, z should be a quadratic non-residue modulo p), and set
(that is, z should be a quadratic non-residue modulo p), and set 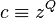 .
. - Let
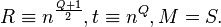
- Loop:
- If
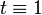 , return R.
, return R. - Otherwise, find the lowest i,
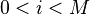 , such that
, such that 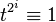 ; e.g. via repeated squaring.
; e.g. via repeated squaring. - Let
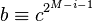 , and set
, and set 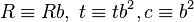 and
and 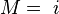 .
.
- If
Once you have solved the congruence with R the second solution is p − R.
Example
Solving the congruence ![]() . It is clear that
. It is clear that ![]() is odd, and since
is odd, and since ![]() , 10 is a quadratic residue (by Euler's criterion).
, 10 is a quadratic residue (by Euler's criterion).
- Step 1: Observe
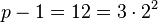 so
so 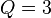 ,
, 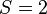 .
.
- Step 2: Take
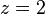 as the quadratic nonresidue (2 is a quadratic nonresidue since
as the quadratic nonresidue (2 is a quadratic nonresidue since 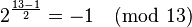 (again, Euler's criterion)). Set
(again, Euler's criterion)). Set 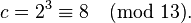
- Step 3:
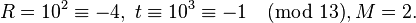
- Step 4: Now we start the loop:
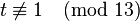 so
so 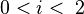 ; i.e.
; i.e. 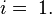
- Let
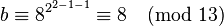 , so
, so 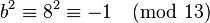 .
. - Set
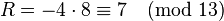 . Set
. Set 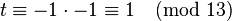 , and
, and 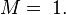
- We restart the loop, and since
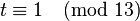 we are done, returning
we are done, returning 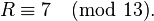
- Let
Indeed, observe that ![]() and naturally also
and naturally also ![]() . So the algorithm yields two solutions to our congruence.
. So the algorithm yields two solutions to our congruence.
Proof
First write ![]() . Now write
. Now write ![]() and
and ![]() , observing that
, observing that ![]() . This latter congruence will be true after every iteration of the algorithm's main loop. If at any point,
. This latter congruence will be true after every iteration of the algorithm's main loop. If at any point, ![]() then
then ![]() and the algorithm terminates with
and the algorithm terminates with ![]() .
.
If ![]() , then consider
, then consider ![]() , a quadratic non-residue of
, a quadratic non-residue of ![]() . Let
. Let ![]() . Then
. Then ![]() and
and ![]() , which shows that the order of
, which shows that the order of ![]() is
is ![]() .
.
Similarly we have ![]() , so the order of
, so the order of ![]() divides
divides ![]() . Suppose the order of
. Suppose the order of ![]() is
is ![]() . Since
. Since ![]() is a square modulo
is a square modulo ![]() ,
, ![]() is also a square, and hence
is also a square, and hence ![]() .
.
Now we set ![]() and with this
and with this ![]() ,
, ![]() and
and ![]() . As before,
. As before, ![]() holds; however with this construction both
holds; however with this construction both ![]() and
and ![]() have order
have order ![]() . This implies that
. This implies that ![]() has order
has order ![]() with
with ![]() .
.
If ![]() then
then ![]() , and the algorithm stops, returning
, and the algorithm stops, returning ![]() . Else, we restart the loop with analogous definitions of
. Else, we restart the loop with analogous definitions of ![]() ,
, ![]() ,
, ![]() and
and ![]() until we arrive at an
until we arrive at an ![]() that equals 0. Since the sequence of S is strictly decreasing the algorithm terminates.
that equals 0. Since the sequence of S is strictly decreasing the algorithm terminates.
//#pragma comment(linker,"/STACK:327680000,327680000") #include#include #include #include #include #include #include <string> #include <set> #include #include #include #include #include
//#pragma comment(linker,"/STACK:327680000,327680000") #include#include #include #include #include #include #include <string> #include <set> #include #include #include #include #include