先看一个例子:
1: DECLARE @Value float
2: SET @Value = 12.1785
3: SELECT '12.1785' as ValueToRound, ROUND(@Value,3) as RoundedValue
4: SET @Value = 12.1745
5: SELECT '12.1745' as ValueToRound,ROUND(@Value,3) as RoundedValue
猜猜看,结果是多少?这个例子源自:T-SQL ROUND Function Bug
1. 问题起因
一个老系统,每个月要对系统发生的每笔业务数据进行汇总,生成应收款;但是每个月累计下来,总会与每天的连续累加汇总差(相差几分钱,或者几毛钱)。
同样的问题还有:仓库里面一批按重量计数的物资,每次出库的时候销账;但偶尔会出现:需要出库的数量,与库存中现有数量一致,但依然无法出库的情况。
问题的根源,就在于数据的存储类型。系统中,选择了使用float来存储数据。但计算机中,是使用近似值来表示float/double的,在这种+/-过程中,误差不断地累积,就出现了上述的这些问题。关于浮点数的存储格式,可以参考我之前的文章:“精确”判断一个浮点数是否等于0
2. Linq to SQL中的Round
知道了问题的原因,我们就可以针对性地进行处理:对数据进行四舍五入后再进行求和。
C#中,提供了两种控制四舍五入的计算方式:MidpointRounding.ToEven和MidpointRounding.AwayFromZero;默认为MidpointRounding.ToEven,即当一个数字是其他两个数字的中间值时,会将其舍入为最接近的偶数。有关舍入方式,可以参考MSDN:“MidpointRounding 枚举”。
值得一提的是,里面对MidpointRounding.AwayFromZero的翻译有误,翻译原文为:“AwayFromZero 当一个数字是其他两个数字的中间值时,会将其舍入为两个值中绝对值较小的值。”但英文原文为:“When a number is halfway between two others, it is rounded toward the nearest number that is away from zero.” 文档描述得相当糟糕,不知道是不是我理解能力太差,反正那一坨东西,绕来绕去,还是看里面举的例子比较靠谱。
1: // 3.4 = Math.Round( 3.45, 1)
2: //-3.4 = Math.Round(-3.45, 1)
3:
4: // 3.4 = Math.Round( 3.45, 1, MidpointRounding.ToEven)
5: // 3.5 = Math.Round( 3.45, 1, MidpointRounding.AwayFromZero)
6:
7: //-3.4 = Math.Round(-3.45, 1, MidpointRounding.ToEven)
8: //-3.5 = Math.Round(-3.45, 1, MidpointRounding.AwayFromZero)
L2S中,如果直接用Math.Round(T.Amount, 2, MidpointRounding.AwayFromZero),则解析成T-SQL就是直接调用Round函数;如果用Math.Round(T.Amount, 2, MidpointRounding.ToEven),则会解析为:
1: (CASE
2: WHEN ((([t0].[Amount]) * 2) = round(([t0].[Amount]) * 2, 2)) AND (([t0].[Amount]) <> round([t0].[Amount], 2)) THEN round(([t0].[Amount]) / 2, 2) * 2
3: ELSE round([t0].[Amount], 2)
4: END)
3. 解决方法
3.1 两次Round
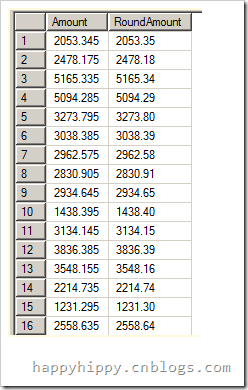
使用一次Round可以解决小数点取舍问题,但无法处理浮点数精度带来的误差,下面是一次Round带来的结果:
这是因为,譬如浮点数2053.345在计算机内部存储的格式可能为2053.2449999999……,一次Round的结果就直接把后面49999…..的给舍掉了。但我们可以使用两次Round来达到需要的舍入效果:Round(Round(Value, 6), 2)
3.2 Decimal
处理精度问题,将数据类型定义为Decimal才是王道。
Decimal在计算及中的存储格式:Decimal 值长度是128位,由 1 位符号、96 位整数以及比例因子组成,比例因子用作 96 位整数的除数并指定整数的哪一部分为小数。比例因子隐式地定为数字 10 的幂,指数范围从 0 到 28。因此,Decimal 值的二进制表示形式为:((-2^96 到 2^96) / 10^(0 到 28))。比例因子还保留 Decimal 数字中的所有尾数零。