论文阅读笔记: Modeling Relational Data with Graph Convolutional Networks

arXiv:1703.06103v4

1.Introduction

主要贡献如下：

• 第一个证明GCN框架可以应用于关系数据建模的工具，特别是链接预测和实体分类任务的工具。
• 介绍了用于参数共享和实施稀疏性约束的技术，并使用它们将R-GCN应用于具有大量关系的多图。
• 展示了以DistMult为例的分解模型的性能，可以通过在关系图中执行多个信息传播步骤的编码器模型来丰富它们，从而显着提高其性能。

2.神经关系建模（Neural relational modeling）

定义有向标签多图(directed and labeled multi-graphs)为$G=(\mathcal{V},\mathcal{E},\mathcal{R})$，包含顶点$v_i\in \mathcal{V}$，和有标签的边（关系）$(v_i,r,v_j)\in \mathcal{E}$，其中的$r\in \mathcal{R}$是一类关系类型。

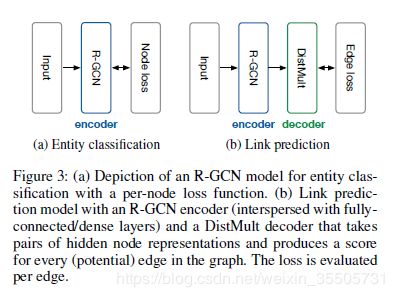
R-GCN模型如下图：

2.1 关系图卷积网络（Relational graph convolutional networks）

一般的图卷积神经网络层结构：
$$h_i^{(l+1)}=\sigma \left(\sum _{m\in {\mathcal{M}}_i}{g}_m(h_i^{(l)},h_j^{(l)})\right)$$
其中${\mathcal{M}}_i$是顶点$v_i$的消息输入顶点集合。$g_m(.,.)$通常选择一个类似于神经网络函数，比如简单线性变换$g_m(h_i,h_j)=W{h}_j$。

论文提出的图卷积神经网络层结构：
$$h_i^{(l+1)}=\sigma \left(\sum _{r\in \mathcal{R}}\sum _{j\in {\mathcal{N}}_i^r}\frac{1}{c_{i,r}}{W}_r^{(l)}{h}_j^{(l)}+W_{r0}^{(l)}{h}_j^{(l)}\right).$$
其中${\mathcal{N}}_i^r$是在关系$r\in \mathcal{R}$下顶点$v_i$的邻居顶点，$c_{i,r}$是归一化因子，可以取$c_{i,r}=|{\mathcal{N}}_i^r|$。

为图中的每个顶点添加自连接。

To ensure that the representation of a node at layer $l+1$ can also be informed by the corresponding representation at layer $l$, we add a single self-connection of a special relation type to each node in the data.

2.2 正则化（Regularization）

R-GCN的两种分离的正则化方法：basis-decomposition 和 block-diagonal-decomposition.

basis-decomposition :
$$W_r^{(l)}=\sum _{b=1}^B{a}_{r,b}^{(l)}{V}_b^{(l)},V_b^{(l)}\in {\mathbb{R}}^{d^{(l+1)}\times d^{(l)}}.$$
$a_{r,b}^{(l)}$是只依赖于$r$的因子。
$W_r^{(l)}$是由$V_b^{(l)}$线性组合。

block-diagonal decomposition ：
$$W_r^{(l)}=\underset{b=1}{\overset{B}{⨁}}{Q}_{b,r}^{(l)},Q_{b,r}^{(l)}\in {\mathbb{R}}^{\frac{d^{(l+1)}}{B}\times \frac{d^{(l)}}{B}}.$$
$W_r^{(l)}$是由$V_b^{(l)}$组成的块对角矩阵$diag(Q_{1,r}^{(l)},\cdots ,Q_{B,r}^{(l)})$。

basis-decomposition可以看作是不同关系类型之间有效权重共享的一种形式，而block-diagonal decomposition可以看作是每种关系类型对权重矩阵的稀疏约束。 块分解结构编码的直觉是，可以将潜在特征分组为变量集，这些变量在组内比在组之间更紧密地耦合。 两种分解都减少了学习高度多关系数据（例如，现实的知识库）所需的参数数量。 同时，我们期望基本参数化可以缓解稀疏关系的过度拟合，因为稀疏关系和更频繁关系之间共享参数更新。

3.实体分类（Entity classification）

最后一层采用$softmax(.)$激活函数，在有标签顶点上使用cross-entropy loss：
$$\mathcal{L}=-\sum _{i\in \mathcal{Y}}\sum _{k=1}^K{t}_{i,k}\ln h_{i,k}^L.$$
其中$\mathcal{Y}$是有标签顶点集，$t_{i,k}$是ground-truth。

4.链接预测（Link prediction）

Link prediction的任务 知识库由一般用有向有标签图$G(\mathcal{V},\mathcal{E},\mathcal{R})$表示,一般提供一个不完全的边子集$\hat{\mathcal{E}}$，需要找到一个分数函数$f(s,r,o)$将边$(s,r,o)$预测为某类的分数。

采用自动编码机模型：

Encoder 将每个实体$v_i\in \mathcal{V}$ 映射到一个实值向量$e_i\in {\mathbb{R}}^d$。

Decoder 解码器根据顶点表示重建图的边，将(subject, relation, object)三元组映射一个实数分数，即$s:{\mathbb{R}}^d\times \mathcal{R}\times {\mathbb{R}}^d\to \mathbb{R}$。

使用DistMult[ang et al. 2014]做解码器，每个关系$r$对应一个对角阵$R_r\in {\mathbb{R}}^{d\times d}$，元组$(s,r,o)$的分数为：
$$f(s,r,o)=e_s^T{R}_r{e}_0.$$

使用负样本训练模型采样。 对于每个观察到的示例，我们进行采$w$个负样本。通过随机破坏每个正面示例的主题或对象来进行采样。 针对交叉熵损失进行了优化，以使模型的可观察三元组得分高于负三元组：
$$\mathcal{L}=-\frac{1}{(1+w)|\hat{\mathcal{E}}|}\sum _{(s,r,o,y)\in \mathcal{T}}y\log l(f(s,r,o))+(1-y)\log \left(1-l(f(s,r,o))\right).$$
其中$\mathcal{T}$是总的样本数（含真实的与破坏得到的负样本），$l$是logistic sigmoid函数，$y$是指示函数，真样本是取值为1，否则为0。

5.对该方法的实验评估

关系抽取实验：

数据集：WordNet(WN18)，Freebase(FB15K)

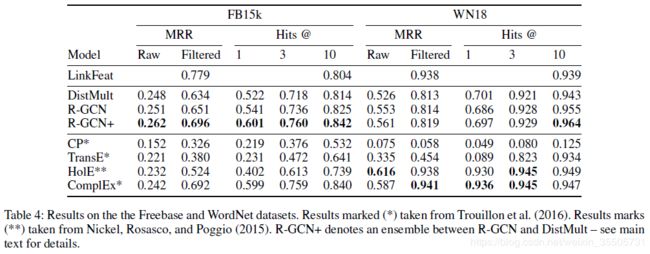
baseline：LinkFeat,DistMult,CP,TransE,HolE,ComplEx

评价准则：MRR(mean reciprocal rank)（Raw，Filtered），Hits @（1，3，10）

结果如下图：

实体分类实验：
数据集：AIFB、MUTAG、BGS、AM

baseline：Feat、WL、RDF2Vec

评价准则：准确率

结果如下图：

参考文献

• Modeling Relational Data with Graph Convolutional Networks
• paperWeekly知识图谱阅读小组-《Modeling Relational Data with Graph Convolutional Networks》
• RGCN - Modeling Relational Data with Graph Convolutional Networks 使用图卷积网络对关系数据进行建模 ESWC 2018
• 利用GCN完善知识库《Modeling Relational Data with Graph Convolutional Networks》