图卷积神经网络GCN---空间卷积层代表作

Spatial-based ConvGNN

1 Convolutional networks on graphs for learning molecular fingerprints

[Duvenaud D, 2015, 1] 是最早对化学上使用图表示分子的文章之一。文章从常见的circular fingerprint作为类比出发，设计了一套类似circular fingerprint的neural graph fingerprint方法，能进行end-to-end学习。

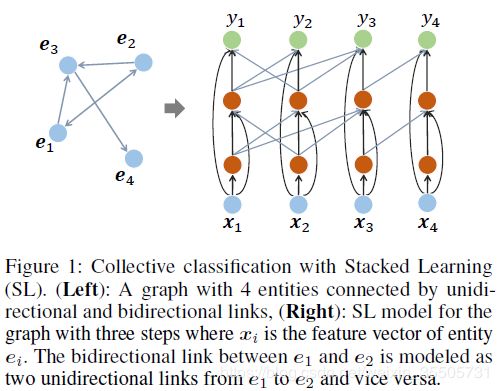
2 Column Networks for Collective Classification

[Pham T, 2017, 2] 考虑了边上的信息：

• contextual features ：

顶点$i$的第$r$个边：
$$c_{i,r}^{(t)}=\frac{1}{|{\mathcal{N}}_{r}i|}\sum _{j\in {\mathcal{N}}_{r}i}{h}_j^{(t-1)}.\text{\hspace{1em}(2.1)}$$

• 卷积 ：

$$h_i^{(t)}=g\left(b^{(t)}+W^{(t)}{h}_i^{(t-1)}+\frac{1}{z}\sum _{r=1}^R{V}_r^{(t)}{c}_{i,r}^{(t)}\right).\text{\hspace{1em}(2.2)}$$
其中$z$是超参。在最后的第$T$步：
$$P(y_i=l)=\text{softmax}\left(b_l+W_l{h}_i^T\right).\text{\hspace{1em}(2.3)}$$

此外，式（2.1）可以加权和：
$$c_{i,r}^{(t)}=\sum _{j\in {\mathcal{N}}_{r}i}{\alpha }_j{h}_j^{(t-1)}.\sum _j{\alpha }_j=1\text{\hspace{1em}(2.4)}$$

原文还给出了跳跃连接：
$$\begin{array}{rl}{h}^{(t)}& =\alpha \odot {\tilde{h}}^{(t)}+(1-\alpha )\odot h^{(t-1)},\\ \alpha & =\sigma \left(b_{\alpha }^{(t)}+W_{\alpha }^{(t)}{h}_i^{(t-1)}+\frac{1}{z}\sum _{r=1}^R{V}_{\alpha r}^{(t)}{c}_{i,r}^{(t)}\right).\end{array}\text{\hspace{1em}(2.5)}$$

3 Learning Convolutional Neural Networks for Graphs

[Niepert M, 2016, 3] 提出的PATCHY-SAN在图上使用传统的CNN。为了能用上CNN，对图结构进行了规范化：固定了图顶点的数量，固定了图顶点的邻居顶点的数量：

• 1.根据label排序后，选择固定的$w$个顶点；
• 2.对于$w$中的每个顶点，使用BFS算法选择至少$k$个邻居顶点；
• 3.根据最佳的排序label选择$k$给邻居顶点进行图规范化。

规范化后，得到顶点、边特征向量长度分别为$a_v,a_e$的两个张量$(w,k,a_v),(w,k,k,a_e)$。将它们reshape成$(wk,a_v),(w{k}^2,a_e)$，将$a_v,a_e$视作通道数，在第一维度上分别做1-D卷积。

最佳的排序label ：
最佳的排序label是指，任意两个图的图距离，和由label决定的邻接矩阵距离最小：
$$\hat{l}=\arg \underset{l}{\min }{\mathbb{E}}_{\mathcal{G}}\left[\left|d_A\left(A^l(G),A^l(G^{{}^{\prime }})\right)-d_G\left(G,G^{{}^{\prime }}\right)\right|\right].$$

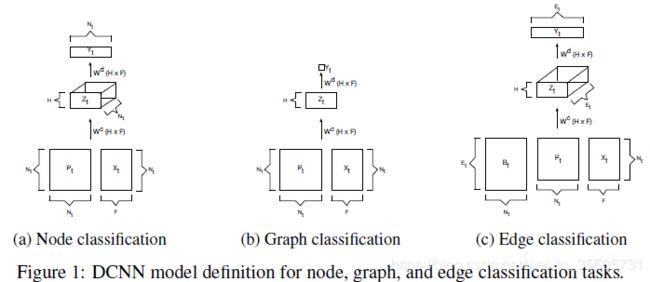
4 Diffusion-Convolutional Neural Networks

[Atwood J, 2016, 4] 根据邻接矩阵$A$计算度归一化的转换矩阵$P_t$，它给出了从顶点$i$跳到顶点$j$的概率。

$P_t^{\ast }$是$P_t\in {\mathbb{R}}^{N_t\times H\times N_t}$的幂级数和，对于顶点分类、图分类、边分类分别有$Z\in {\mathbb{R}}^{N_t\times H\times F},{\mathbb{R}}^{H\times F},{\mathbb{R}}^{M_t\times H\times F}$。$X_t\in {\mathbb{R}}^{N_t\times F}$

• Node Classification ：

$$\begin{array}{rl}{Z}_{t,ijk}& =f\left(W_{jk}^c\sum _{l=1}^{N_t}{P}_{t,ijl}^{\ast }{X}_{t,lk}\right),\\ \text{即：}{Z}_t& =f\left(W^c\odot P_t^{\ast }{X}_t\right).\end{array}\text{\hspace{1em}(4.1)}$$
其中$W^c\in {\mathbb{R}}^{H\times F}$。

输出：
$$\begin{array}{rl}\hat{Y}& =\arg \max \left(f(W^D\odot Z)\right),\\ \mathbb{P}(Y|X)& =\text{softmax}\left(f(W^D\odot Z)\right).\end{array}\text{\hspace{1em}(4.2)}$$

• Graph Classification ：

$$Z_t=f\left(W^c\odot \frac{1_{N_t}^T{P}_t^{\ast }{X}_t}{N_t}\right).\text{\hspace{1em}(4.3)}$$

• Edge Classification and Edge Features ：

用
$$A_t^{{}^{\prime }}=\left(\begin{array}{cc}{A}_t& B_t^T\\ B_t& 0\end{array}\right)\text{\hspace{1em}(4.4)}$$
计算$P_t^{{}^{\prime }}$代替$P_t$做卷积取分类顶点或边。

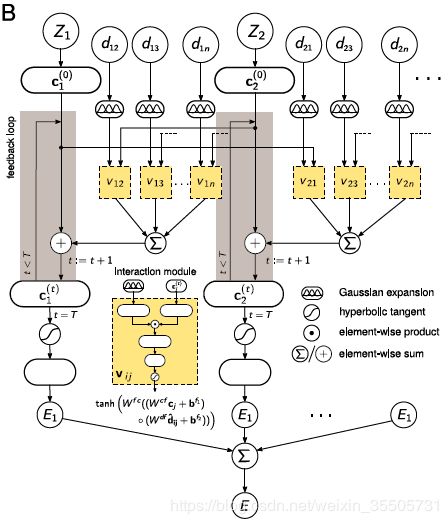
5 Quantum-Chemical Insights from Deep Tensor Neural Networks

[Schutt K T, 2017, 5] 聚合了顶点和边的信息。用高斯核对顶点$V$构造距离矩阵$D=({\hat{d}}_{ij}{)}_{|V|\times |V|}$。记每个顶点$v_i\in V$的特征向量为$x_i$，每条$e_{ij}\in E$上的特征向量为$y_{ij}$表示顶点$v_j$对$v_i$的作用。

• 顶点特征向量$x_i$更新：

$$x_i^{(t+1)}=x_i^{(t)}+\sum _{j\ne i}{y}_{ij}.\text{\hspace{1em}(5.1)}$$

• 边特征向量$y_{ij}$更新：

$$y_{ij}=\tanh \left[W^{fc}\left(\left(W^{cf}{x}_j+v^{f_1}\right)\odot \left(W^{df}{\hat{d}}_{ij}+v^{f_2}\right)\right)\right].\text{\hspace{1em}(5.2)}$$

6 Interaction Networks for Learning about Objects, Relations and Physics

[Battaglia P W, 2016, 6] 将图网络应用于自然科学中。IN模块为：
$$\begin{array}{rl}IN(G)& ={\varphi }_O\left(a\left(G,X,{\varphi }_R\left(m(G)\right)\right)\right);\\ m(G)& =B=\{b_k{\}}_{k=1,\cdots ,N_R}\\ {\varphi }_R(B)& =E=\{e_k{\}}_{k=1,\cdots ,N_R}\\ a(G,X,E)& =C=\{c_j{\}}_{j=1,\cdots ,N_O}\\ {\varphi }_O(C)& =P=\{p_j{\}}_{j=1,\cdots ,N_O}\end{array}\text{\hspace{1em}(6.1)}$$

记$N_O$表示顶点的个数，$N_R$表示边（关系）的个数，$D_S,D_R$分别表示顶点、边的特征向量长度。那么$O\in {\mathbb{R}}^{D_S\times N_O}$表示所有顶点的特征列向量组成的矩阵，$R_a\in {\mathbb{R}}^{D_R\times N_R}$表示所有边的特征列向量组成的矩阵。将顶点编号，用0-1表示接受矩阵$R_r\in {\mathbb{R}}^{N_O\times N_R}$和发射矩阵$R_s\in {\mathbb{R}}^{N_O\times N_R}$。

用多层全连接实现${\varphi }_R,{\varphi }_O$：
$$\begin{array}{rlr}B& =m(G)=[O{R}_r;O{R}_s;R_a]& \in {\mathbb{R}}^{(2D_S+D_R)\times N_R}\\ E& ={\varphi }_R(B)& \in {\mathbb{R}}^{D_E\times N_R}\\ \bar{E}& =E{R}_r^T& \in {\mathbb{R}}^{D_E\times N_O}\\ C& =a(G,X,E)=[O;X;\bar{E}]& \in {\mathbb{R}}^{(D_S+D_X+D_E)\times N_O}\\ P& ={\varphi }_O(C)& \in {\mathbb{R}}^{D_P\times N_O}\end{array}\text{\hspace{1em}(6.2)}$$

7 Geometric deep learning on graphs and manifolds using mixture model cnns

[F. Monti, 2017, 7] 提出了能再流形和图上混合使用的卷积。对于每个顶点$x$的邻居点$y\in \mathcal{N}(x)$都用伪坐标向量$u(x,y)$将它们关联。定义由可学习参数$\Theta$决定的权重函数$w_{\Theta }(u)=(w_1(u),\cdots ,w_J(u))$：
$$D_j(x)f=\sum _{y\in \mathcal{N}(x)}{w}_j(u(x,y))f(y),j=1,\cdots ,J.\text{\hspace{1em}(7.1)}$$
其中$J$代表提取的patch的维数。原文里$w_j(u)$选的是由可学习的${\Sigma }_j,{\mu }_j$决定的高斯核：
$$w_j(u)=\exp \left(-\frac{1}{2}{\left(u-{\mu }_j\right)}^T{\Sigma }_j^{-1}\left(u-{\mu }_j\right)\right).\text{\hspace{1em}(7.2)}$$
那么卷积操作为：
$$\left(f\star g\right)(x)=\sum _{j=1}^J{g}_j{D}_j(x)f.\text{\hspace{1em}(7.3)}$$

8 Molecular Graph Convolutions: Moving Beyond Fingerprints

[Kearnes S, 2017, 8] 提出了图上建模的三个性质：

• Property 1 (Order invariance). The output of the model should be invariant to the order that the atom and bond information is encoded in the input.

• Property 2 (Atom and pair permutation invariance). The values of an atom layer and pair permute with the original input layer order. More precisely, if the inputs are permuted with a permutation operator $Q$, then for all layers $x$, $y$, $A^x$ and $P^y$ are permuted with operator $Q$ as well.

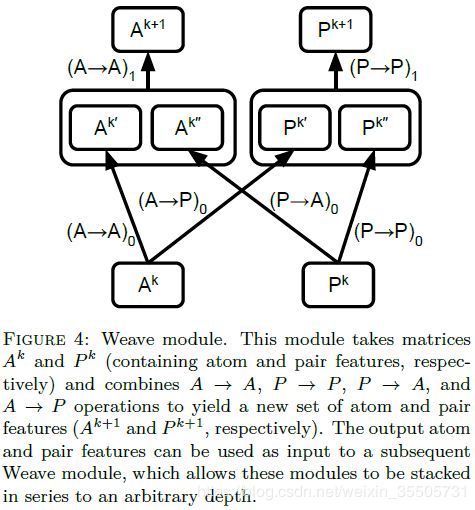
• Property 3 (Pair order invariance). For all pair layers $y$, $P_{(a,b)}^y=P_{(b,a)}^y$

$A^x,p^y$分别表示原子层（atom）、键对层（pair）的第$x$、$y$层的值。网络由4个主要操作组成：

• ($A\to A$) ：

$$A_a^y=f\left(A_a^{x1},A_a^{x2},\cdots ,A_a^{xn}\right).\text{\hspace{1em}(8.1)}$$

• ($A\to P$) ：

$$P_{a,b}^y=g\left(f\left(A_a^x,A_b^x\right),f\left(A_b^x,A_a^x\right)\right).\text{\hspace{1em}(8.2)}$$

• ($P\to A$) ：

$$A_a^y=g\left(f\left(P_{(a,b)}^x\right),f\left(P_{(a,c)}^x\right),f\left(P_{(a,d)}^x\right),\cdots \right).\text{\hspace{1em}(8.3)}$$

• ($P\to P$) ：

$$P_{a,b}^y=f\left(P_{a,b}^{x1},P_{a,b}^{x2},\cdots ,P_{a,b}^{xn}\right).\text{\hspace{1em}(8.4)}$$

其中$f(\cdot ),g(\cdot )$表示任意函数和任意的commutative函数。

9 Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs

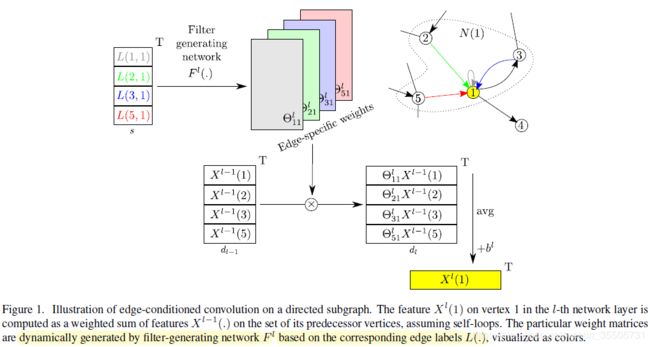
[Simonovsky M, 2017, 9] 用边的特征做构造顶点的卷积权重。对于边的特征$L(j,i)\in {\mathbb{R}}^s$:
$${\Theta }_{ji}^l=F^l(L(j,i))\in {\mathbb{R}}^{d_l\times d_{l-1}}.\text{\hspace{1em}(9.1)}$$

卷积为：
$$\begin{array}{rl}{X}^l(i)& =\frac{1}{|\mathcal{N}(i)|}\sum _{j\in \mathcal{N}(i)}{F}^l(L(j,i))X^{l-1}(j)+b^l,\\ & =\frac{1}{|\mathcal{N}(i)|}\sum _{j\in \mathcal{N}(i)}{\Theta }_{ji}^l{X}^{l-1}(j)+b^l.\end{array}\text{\hspace{1em}(9.2)}$$

原文提到的池化方法：

• 1.下采样或者合并顶点
• 2.创建新的边缘结构$E^{(h)}$并标记$L^{(h)}$（所谓的约简）
• 3.将原来的顶点映射到新的顶点上$M^{(h)}:V^{(h-1)}\to V^{(h)}$。

10 Neural Message Passing for Quantum Chemistry

[Gilmer J, 2017, 10] 提出的是一个MPNN框架，将GNN分成了两个阶段：消息传播阶段和读出阶段。

• message passing phase ：

消息传播阶段又由两部分组成，一是将顶点的邻居顶点和相连边的特征聚合$M_t(\cdot )$（message function），二是对顶点更新$U_t(\cdot )$（vertex update function）：
$$\begin{array}{rl}{m}_v^{(t+1)}& =\sum _{w\in \mathcal{N}(v)}{M}_t\left(h_v^{(t)},h_w^{(t)},e_{vw}\right),\\ h_v^{(t+1)}& =U_t\left(h_v^{(t)},m_v^{(t+1)}\right).\end{array}\text{\hspace{1em}(10.1)}$$

• readout phase：

对图上每个顶点最后使用读出函数$R(\cdot )$：
$$\hat{y}=R\left(\{h_v^{(T)}|v\in {\mathcal{V}}_G\}\right).\text{\hspace{1em}(10.2)}$$

11 Inductive Representation Learning on Large Graphs

[Hamilton W L, 2017, 11] 提出的方法叫GraphSAGE,可扩展性更强，对于节点分类和链接预测问题的表现也比较突出。同样，GraphSAGE也可以用MPNN框架描述：

• 消息聚合：

$$h_{\mathcal{N}(v)}^{(k)}\leftarrow {\text{AGGREGATE}}_k\left(h_u^{(k-1)},\forall u\in \mathcal{N}(v)\right).\text{\hspace{1em}(11.1)}$$

• 顶点特征更新：

$$\begin{array}{rl}{h}_v^{(k)}& \leftarrow \sigma \left(W^{(k)}\cdot \text{CONCAT}\left(h_v^{(k-1)},h_{\mathcal{N}(v)}^{(k)}\right)\right).\\ h_v^{(k)}& \leftarrow \frac{h_v^{(k)}}{\Vert h_v^{(k)}{\Vert }_2},\forall v\in \mathcal{V}.\end{array}\text{\hspace{1em}(11.2)}$$

• 读出函数：

$$z_v\leftarrow h_v^{(K)},\forall v\in \mathcal{V}.\text{\hspace{1em}(11.3)}$$

原文给出了三种聚合函数：

• Mean aggregator：

$$h_v^{(k)}\leftarrow \sigma \left(W\cdot \text{MEAN}\left(\{h_v^{(k-1)}\}\cup \{h_u^{(k-1)},\forall u\in \mathcal{N}(v)\}\right)\right).\text{\hspace{1em}(11.4)}$$

• LSTM aggregator.

• Pooling aggregator：

$${\text{AGGREGATE}}_k^{\text{pool}}=\max \left(\left\{\sigma \left(W_{\text{pool}}{h}_{u_i}^k+b\right),\forall u_i\in \mathcal{N}(v)\right\}\right).\text{\hspace{1em}(11.5)}$$

其中$W_{\text{pool}}$是可学习的参数。

12 Robust Spatial Filtering With Graph Convolutional Neural Networks

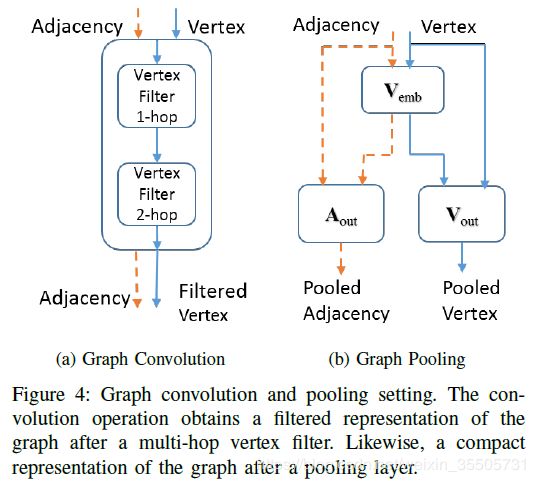
[Such F P, 2017, 12] 提出的网络能够适用于同质或异质的图数据集。

对于不同的特征可以定义不同的邻接矩阵，将这些邻接矩阵组成$\mathcal{A}=(A_1,\cdots ,A_L)\in {\mathbb{R}}^{N\times N\times L}$。

卷积核$H\in {\mathbb{R}}^{N\times N\times C}$为：
$$H^{(c)}\approx \sum _{l=1}^L{h}_l^{(c)}{A}_l.\text{\hspace{1em}(12.1)}$$

卷积操作为：
$$V_{\text{out}}=\sum _{c=1}^C{H}^{(c)}{V}_{\text{in}}^{(c)}+b.\text{\hspace{1em}(12.2)}$$

图嵌入池化过程。为了得到$V_{emb}\in {\mathbb{R}}^{N\times N^{{}^{\prime }}}$使用卷积核$H_{emb}\in {\mathbb{R}}^{N\times N\times C\times N^{{}^{\prime }}}$：
$$\begin{array}{rl}{V}_{emb}^{(n^{{}^{\prime }})}& =\sum _c^C{H}_{emb}^{(c,n^{{}^{\prime }})}{V}_{in}^{(c)}+b,\\ V_{emb}^{\ast }& =\sigma (V_{emb}),\\ V_{out}& =V_{emb}^{\ast T}{V}_{in},\\ A_{out}& =V_{emb}^{\ast T}{A}_{in}{V}_{emb}^{\ast }\end{array}\text{\hspace{1em}(12.3)}$$

13 Large-Scale Learnable Graph Convolutional Networks

[Gao H, 2018, 13] 同样是在顶点特征向量上使用传统的CNN。

设第$l$层的图顶点特征向量长度为$F_l$，每个顶点选择$k$个邻居点。

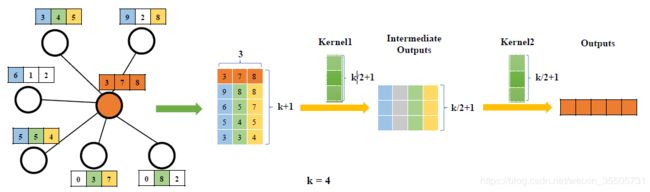
卷积过程：

1. 将每个顶点的邻居$\mathcal{N}$的特征向量拼接成张量${\mathbb{R}}^{|\mathcal{N}|\times F_l}$；
2. 将张量${\mathbb{R}}^{|\mathcal{N}|\times F_l}$的每列从大到小排序，然后截取前$k$个，得${\mathbb{R}}^{k\times F_l}$；
3. 再和顶点的特征向量拼接为${\mathbb{R}}^{(k+1)\times F_l}$；
4. $CON{V}_1:{\mathbb{R}}^{(k+1)\times F_l}\to {\mathbb{R}}^{(\frac{k}{2}+1)\times k}$；
5. $CON{V}_2:{\mathbb{R}}^{(\frac{k}{2}+1)\times k}\to {\mathbb{R}}^{1\times F_{l+1}}$。

14 Signed Graph Convolutional Network

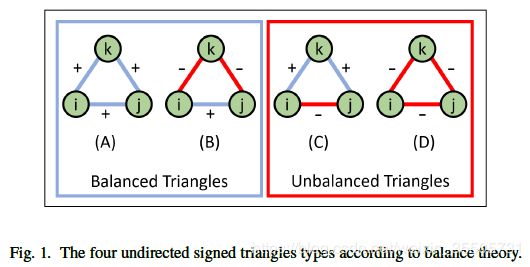
[Derr T, 2018, 14] 提出了在有符号的图数据上建立神经网络。在无符号的图中卷积一般是聚合邻居顶点的信息，但是由于在有符号的图上有正有负，含义不同，需要将图分成平衡路径和非平衡路径。

分解利用了平衡理论，直观的讲就是：1）朋友的朋友，就是我的朋友，2）敌人的朋友就是我的敌人。 平衡的部分包含偶数条负连接，反之，包含奇数条负链接，被认为是不平衡。见下图

分解后，分别做卷积聚合，平衡部分：
$$h_i^{B(l)}=\{\begin{array}{l}\sigma \left(W^{B(1)}\left[{\sum }_{j\in {\mathcal{N}}_i^{+}}\frac{h_j^{(0)}}{|{\mathcal{N}}_i^{+}|},h_i^{(0)}\right]\right)l=1;\\ \sigma \left(W^{B(l)}\left[{\sum }_{j\in {\mathcal{N}}_i^{+}}\frac{h_j^{B(l-1)}}{|{\mathcal{N}}_i^{+}|},{\sum }_{k\in {\mathcal{N}}_i^{-}}\frac{h_k^{U(l-1)}}{|{\mathcal{N}}_i^{-}|},h_i^{B(l-1)}\right]\right)l\ne 1.\end{array}\text{\hspace{1em}(14.1)}$$

非平衡部分：
$$h_i^{U(l)}=\{\begin{array}{l}\sigma \left(W^{U(1)}\left[{\sum }_{j\in {\mathcal{N}}_i^{-}}\frac{h_j^{(0)}}{|{\mathcal{N}}_i^{-}|},h_i^{(0)}\right]\right)l=1;\\ \sigma \left(W^{U(l)}\left[{\sum }_{j\in {\mathcal{N}}_i^{+}}\frac{h_j^{U(l-1)}}{|{\mathcal{N}}_i^{+}|},{\sum }_{k\in {\mathcal{N}}_i^{-}}\frac{h_k^{B(l-1)}}{|{\mathcal{N}}_i^{-}|},h_i^{U(l-1)}\right]\right)l\ne 1.\end{array}\text{\hspace{1em}(14.2)}$$

读出：
$$z_i\leftarrow [h_i^{B(L)},h_i^{U(L)}],\forall u_i\in \mathcal{U}.\text{\hspace{1em}(14.3)}$$

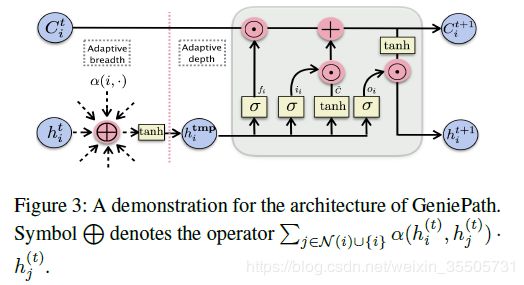
15 GeniePath: Graph Neural Networks with Adaptive Receptive Paths

[Liu Z, 2018, 15] 提出了在广度和深度自适应选择顶点经行特征聚合。

• Adaptive Breadth：

基于GAT学习一跳邻居（隐）特征的重要性，决定继续探索的方向:
$$h_i^{(\text{tmp})}=\tanh \left({W^{(t)}}^T\sum _{j\in \mathcal{N}(i)\cup \{i\}}\alpha \left(h_i^{(t)},h_j^{(t)}\right)\cdot h_j^{(t)}\right).\text{\hspace{1em}(15.1)}$$
其中$\alpha \left(h_i^{(t)},h_j^{(t)}\right)$是注意力机制：
$$\begin{array}{rl}\alpha (x,y)& ={\text{softmax}}_y\left(v^T\tanh \left(W_s^{T}x+W_d^{T}y\right)\right),\\ {\text{softmax}}_y(\cdot ,y)& =\frac{\exp f(\cdot ,y)}{{\sum }_{y^{{}^{\prime }}}\exp f(\cdot ,y^{{}^{\prime }})}.\end{array}\text{\hspace{1em}(15.2)}$$

• Adaptive Depth：

$$\begin{array}{rl}{i}_i& =\sigma \left({W_i^{(t)}}^T{h}_i^{(\text{tmp})}\right),\\ f_i& =\sigma \left({W_f^{(t)}}^T{h}_i^{(\text{tmp})}\right),\\ o_i& =\sigma \left({W_o^{(t)}}^T{h}_i^{(\text{tmp})}\right),\\ C& =\tanh \left({W_c^{(t)}}^T{h}_i^{(\text{tmp})}\right),\\ C_i^{(t+1)}& =f_i\odot C_i^{(t)}+i_i\odot C,\\ h_t^{(t+1)}& =o_i\odot \tanh (C_i^{(t+1)}).\end{array}\text{\hspace{1em}(15.3)}$$

原文给出了一个变体：
$$\begin{array}{rl}{\mu }_i^{(0)}& =W_x^T{X}_i,\\ i_i& =\sigma \left({W_i^{(t)}}^T\text{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right),\\ f_i& =\sigma \left({W_f^{(t)}}^T\text{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right),\\ o_i& =\sigma \left({W_o^{(t)}}^T\text{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right),\\ C& =\tanh \left({W_c^{(t)}}^T\text{CONCAT}\left(h_i^{(t)},{\mu }_i^{(t)}\right)\right),\\ C_i^{(t+1)}& =f_i\odot C_i^{(t)}+i_i\odot C,\\ {\mu }_t^{(t+1)}& =o_i\odot \tanh (C_i^{(t+1)}).\end{array}$$

16 Fast Learning with Graph Convolutional Networks via Importance Sampling

[Chen J, 2018, 16] 为了加快训练速度，提出了采样方法，即选取一部分顶点参与训练。

下图算法是随机采样：

下图是论文中提出的采用重要性采样，原文证明能有更小的方差：

其中的采样概率为：
$$q(u)=\frac{\Vert \hat{A}(:,u){\Vert }^2}{{\sum }_{u^{{}^{\prime }}\in \mathcal{V}}\Vert \hat{A}(:,u^{{}^{\prime }}){\Vert }^2},u\in \mathcal{V}.\text{\hspace{1em}(16.1)}$$

17 Stochastic Training of Graph Convolutional Networks with Variance Reduction

[Chen J, 2018, 17] 证明[Chen J, 2018, 16]的重要性采样方法在实践中并不好，因为有的顶点可能有很多采样点而另一些顶点可能没有采样点。

$\hat{A}=A+I_N,{\hat{D}}_{vv}={\sum }_u{\hat{A}}_{uv},P={\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}$。$\hat{P}$是$P$的无偏估计${\hat{P}}_{uv}^{(l)}=\frac{|\mathcal{N}(u)|}{D^{(l)}}{P}_{uv}$，原文将$h_v^{(l)}$分解成$h_v^{(l)}=\Delta h_v^{(l)}+{\bar{h}}_v^{(l)}$。原始的卷积中$h_v^{(l)}$的递归计算导致计算量过大，[Chen J, 2018, 17]将每层得到的$h_v^{(l)}$计算${\bar{h}}_v^{(l)}$用于保存做历史的近似。
$$\begin{array}{rl}(P{H}^{(l)}{)}_u& =\sum _{v\in \mathcal{N}(u)}{P}_{uv}\Delta h_v^{(l)}+\sum _{v\in \mathcal{N}(u)}{P}_{uv}{\bar{h}}_v^{(l)},\\ & \approx \frac{|\mathcal{N}(u)|}{D^{(l)}}\sum _{v\in \hat{\mathcal{N}}(u)}{P}_{uv}\Delta h_v^{(l)}+\sum _{v\in \mathcal{N}(u)}{P}_{uv}{\bar{h}}_v^{(l)}.\end{array}$$
也就是，随机选取近邻节点所得到的项是$\Delta h_v^{(l)}$。

卷积为：
$$Z^{(l+1)}=\left({\hat{P}}^{(l)}\left(H^{(l)}-{\bar{H}}^{(l)}\right)+P{\bar{H}}^{(l)}\right)W^{(l)}\text{\hspace{1em}(17.1)}$$

Stochastic GCN:

1. 随机选择一个小批量顶点集${\mathcal{V}}_B\in {\mathcal{V}}_L$;
2. 建立一个仅包含当前小批量所需的激活$h_v^{(l)}$和${\bar{h}}_v^{(l)}$的计算图；
3. 通过等式(17.1)正向传播获得预测；
4. 通过向后传播获取梯度，并通过SGD更新参数；
5. 更新历史激活值。

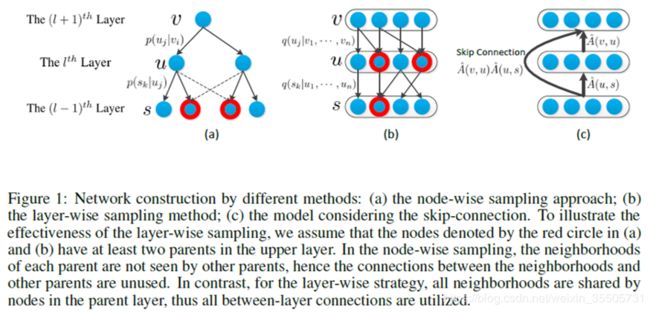
18 Adaptive Sampling Towards Fast Graph Representation Learning

[Huang W, 2018, 18]

一般的卷积：
$$h^{(l+1)}(v_i)=\sigma \left(\sum _{j=1}^N\hat{a}(v_i,u_j)h^{(l)}(u_j)W^{(l)}\right),i=1,\cdots ,N.\text{\hspace{1em}(18.1)}$$

• Node-Wise Sampling ：

将式（18.1）改写为：
$$\begin{array}{rl}{h}^{(l+1)}(v_i)& =\sigma \left(\left(\sum _{j=1}^N\hat{a}(v_i,u_j)\right)\left(\sum _{j=1}^N\frac{\hat{a}(v_i,u_j)}{{\sum }_{j=1}^N\hat{a}(v_i,u_j)}\right)h^{(l)}(u_j)W^{(l)}\right),,\\ & \stackrel{N(v_i):={\sum }_{j=1}^N\hat{a}(v_i,u_j)}{=}\sigma \left(N(v_i)\left(\sum _{j=1}^N\frac{\hat{a}(v_i,u_j)}{N(v_i)}\right)h^{(l)}(u_j)W^{(l)}\right),\\ & \stackrel{p(u_j|v_i):=\frac{\hat{a}(v_i,u_j)}{N(v_i)}}{=}\sigma \left(N(v_i)\left(\sum _{j=1}^{N}p(u_j|v_i)h^{(l)}(u_j)\right)W^{(l)}\right),\\ & =\sigma \left(N(v_i){\mathbb{E}}_{p(u_j|v_i)}\left[h^{(l)}(u_j)\right]W^{(l)}\right),i=1,\cdots ,N.\end{array}\text{\hspace{1em}(18.2)}$$

使用Monte-Carlo sampling，${\mu }_p(v_i)={\mathbb{E}}_{p(u_j|v_i)}\left[h^{(l)}(u_j)\right]$：
$${\hat{\mu }}_p(v_i)=\frac{1}{n}\sum _{j=1}^n{h}^{(l)}({\hat{u}}_j),{\hat{u}}_j\sim p(u_j|v_i).\text{\hspace{1em}(18.3)}$$

• Layer-Wise Sampling ：
  同样地：
  $$h^{(l+1)}(v_i)=\sigma \left(N(v_i){\mathbb{E}}_{q(u_j|v_1,\cdots ,v_n)}\left[\frac{p(u_j|v_i)}{q(u_j|v_1,\cdots ,v_n)}{h}^{(l)}(u_j)\right]W^{(l)}\right),i=1,\cdots ,N.\text{\hspace{1em}(18.4)}$$
  同样Monte-Carlo sampling，${\mu }_q(v_i)={\mathbb{E}}_{q(u_j|v_1,\cdots ,v_n)}\left[\frac{p(u_j|v_i)}{q(u_j|v_1,\cdots ,v_n)}{h}^{(l)}(u_j)\right]$：
  $${\hat{\mu }}_q(v_i)=\frac{1}{n}\sum _{j=1}^n\frac{p({\hat{u}}_j|v_i)}{q({\hat{u}}_j|v_1,\cdots ,v_n)}{h}^{(l)}({\hat{u}}_j),{\hat{\mu }}_j\sim q({\hat{u}}_j|v_1,\cdots ,v_n).\text{\hspace{1em}(18.5)}$$

原文给了$q(u_j)$最佳取法：
$$q^{\ast }(u_j)=\frac{{\sum }_{i=1}^{n}p(u_j|v_i)|g(x(u_j))|}{{\sum }_{j=1}^N{\sum }_{i=1}^{n}p(u_j|v_i)|g(x(u_j))|}.\text{\hspace{1em}(18.6)}$$
其中$g(\cdot )$是线性行数。

参考文献

• 1 Duvenaud D, Maclaurin D, Aguileraiparraguirre J, et al. Convolutional networks on graphs for learning molecular fingerprints[C]. neural information processing systems, 2015: 2224-2232.

• 2 Pham T, Tran T, Phung D, et al. Column Networks for Collective Classification[C]. national conference on artificial intelligence, 2017: 2485-2491.

• 3 Niepert M, Ahmed M H, Kutzkov K, et al. Learning Convolutional Neural Networks for Graphs[J]. arXiv: Learning, 2016.

• 4 Atwood J, Towsley D. Diffusion-Convolutional Neural Networks[C]. neural information processing systems, 2016: 1993-2001.

• 5 Schutt K T, Arbabzadah F, Chmiela S, et al. Quantum-chemical insights from deep tensor neural networks[J]. Nature Communications, 2017, 8(1): 13890-13890.

• 6 Battaglia P W, Pascanu R, Lai M, et al. Interaction networks for learning about objects, relations and physics[C]. neural information processing systems, 2016: 4509-4517.

• 7 F. Monti, D. Boscaini, J. Masci, E. Rodola, J. Svoboda, and M. M.Bronstein, “Geometric deep learning on graphs and manifolds using mixture model cnns,” in Proc. of CVPR, 2017, pp. 5115–5124.

• 8 Kearnes S, Mccloskey K, Berndl M, et al. Molecular graph convolutions: moving beyond fingerprints[J]. Journal of Computer-aided Molecular Design, 2016, 30(8): 595-608.

• 9 Simonovsky M, Komodakis N. Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs[C]. computer vision and pattern recognition, 2017: 29-38.

• 10 Gilmer J, Schoenholz S S, Riley P, et al. Neural Message Passing for Quantum Chemistry[C]. international conference on machine learning, 2017: 1263-1272.

• 11 Hamilton W L, Ying Z, Leskovec J, et al. Inductive Representation Learning on Large Graphs[C]. neural information processing systems, 2017: 1024-1034.

• 12 Such F P, Sah S, Dominguez M, et al. Robust Spatial Filtering With Graph Convolutional Neural Networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(6): 884-896.

• 13 Gao H, Wang Z, Ji S, et al. Large-Scale Learnable Graph Convolutional Networks[C]. knowledge discovery and data mining, 2018: 1416-1424.

• 14 Derr T, Ma Y, Tang J, et al. Signed Graph Convolutional Network.[J]. arXiv: Social and Information Networks, 2018.

• 15 Liu Z, Chen C, Li L, et al. GeniePath: Graph Neural Networks with Adaptive Receptive Paths.[J]. arXiv: Learning, 2018.

• 16 Chen J, Ma T, Xiao C, et al. FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling[C]. international conference on learning representations, 2018.

• 17 Chen J, Zhu J, Song L, et al. Stochastic Training of Graph Convolutional Networks with Variance Reduction[C]. international conference on machine learning, 2018: 941-949.

• 18 Huang W, Zhang T, Rong Y, et al. Adaptive Sampling Towards Fast Graph Representation Learning[C]. neural information processing systems, 2018: 4558-4567.