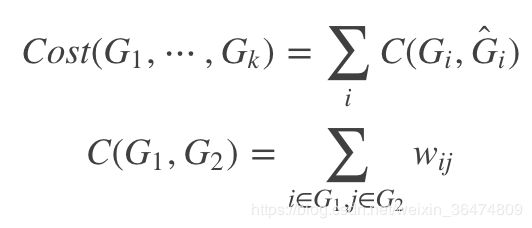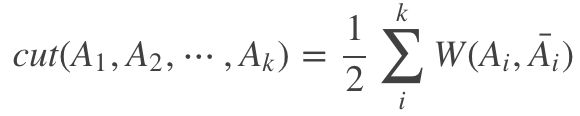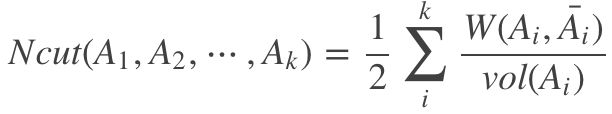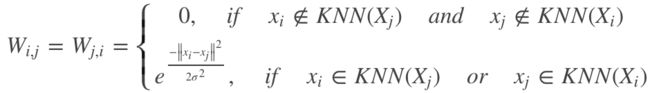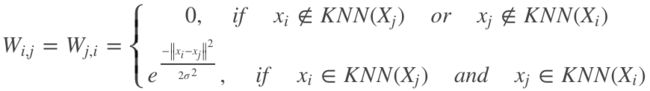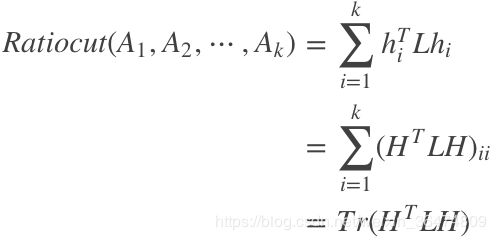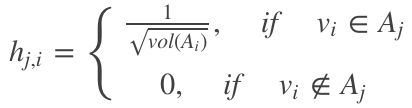Graph特征提取方法:谱聚类(Spectral Clustering)详解
背景：Graph的特征提取方法有很多种，有空域的方法vertex domain，谱方法spectral domain，最经典的就是图卷积GCN（Graph Convolutional Network）GCN (Graph Convolutional Network) 图卷积网络解析 。这里是另一种方法，谱聚类的方法( spectral clustering)。
相关论文详解：
GCN (Graph Convolutional Network) 图卷积网络概览
图注意力网络(GAT) ICLR2018, Graph Attention Network论文详解
旷视CVPR2019图卷积多标签图像识别Multi-Label Image Recognition with Graph Convolutional Networks论文详解
无监督图嵌入Unsupervised graph embedding|基于对抗的图对齐adversarial graph alignment详解
Graph特征提取方法:谱聚类(Spectral Clustering)详解
目录
一、问题描述
1.1 无向图及其矩阵
图的特征提取方法
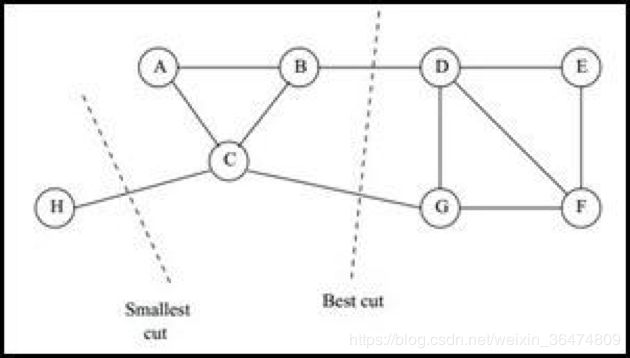
1.2 切图(节点分类)
1.3 分割后cut（cost）
1.4 另两种切图cut
直接cut的缺点
RatioCut与Ncut
二、相似度矩阵
2.1 相似度矩阵
2.2 ε-近邻法（ε-neighborhood graph）
2.3 k近邻法（k-nearest nerghbor graph）
2.4 全连接法（fully connected graph）
三、切图方法理论推导
3.1 最小化Ratio Cut
3.2 指引向量H
3.3 结论
3.4 Ncut 同理
四、算法流程
4.1 输入输出
4.2 流程
参考
一、问题描述
https://blog.csdn.net/songbinxu/article/details/80838865
聚类属于无监督学习，这个相当于将聚类的方法用到Graph上。因为不是欧几里得空间里面处理数据，所以需要用到Graph的知识来进行聚类。
1.1 无向图及其矩阵
针对，无向图，带权重图像
拉普拉斯矩阵：
关于拉普拉斯矩阵与图的关系，可以参见：GCN (Graph Convolutional Network) 图卷积网络解析
对于图 G=(V,E)，其Laplacian 矩阵的定义为 L=D-A ，
- L为拉普拉斯矩阵Laplacian matrix
- D为对角度矩阵Degree matrix，对角线上的元素是顶点的度，即该元素链接的元素的个数
- A为邻接矩阵 Adjacency matrix ,即表示任意两个顶点之间的邻接关系，邻接则为1，不邻接则为0
权重矩阵：
每一条边上的权重wij为两个顶点的相似度，从而可以定义相似度矩阵W，这个矩阵即描述所有节点之间关系的矩阵。类似于邻接矩阵。
图的特征提取方法
空域方法：
vertex domain(spatial domain)，很直观，直接用相应顶点连接的neighbors来提取特征。
Learning Convolutional Neural Networks for Graphs http://proceedings.mlr.press/v48/niepert16.pdf
频域方法：
GCN，GAT的方法，即图卷积网络所采用的方法。
GCN (Graph Convolutional Network) 图卷积网络解析
图注意力网络(GAT) ICLR2018, Graph Attention Network论文详解
普聚类Spectral clustering：
即这篇文章所讲的方法
1.2 切图(节点分类)
也叫图分割，相当于把一个图分成许多个子图。
一个图G可能有很多个子图Gi（总共k个），子图之间没有交集。但是所有子图并在一起得到图G
简而言之，就是图分割成子图之后，分割不重不漏： Gi∩Gj=∅,且G1∪G2∪...∪Gk=G，
1.3 分割后cut（cost）
根据分割的方法，可以算出一个cost。
- Gi与
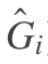互为补集合 - C()表示cost函数，
表示第i个子图与其补集之间的cost - 整个分割的cost表示为所有分割后的子图与其补集合之间cost的和
- C(G1,G2)表示子图G1和子图G2的cost为两图之间所有节点的w
- w可以理解为两个节点之间的相似程度，也可以理解成节点间的邻接矩阵，我们后面细细讨论w
这样，我们根据w定义了图的分割的cost，下面我们图的聚类问题，转换为了最小化cost的问题。
也有将上面写成这样的：
很好理解，与上个公式一样，Ai就是切出来的子图，
为其补集，只不过这里多了个1/2
1.4 另两种切图cut
直接cut的缺点
安装上面的cut，容易造成一种现象，会造成将图G切成很多个单点离散的图。就是每个节点切成一个图，切出的子图过多。为什么会这样：
每个子图切成一个类，则
需要遍历的m就少，更容易满足最小化cut。
RatioCut与Ncut
显然这样是最快且最能满足那个最小化操作的，但这明显不是想要的结果，所以有了RatioCut和Ncut
- 其中|Ai| 为Ai中点的个数，vol(Ai)为Ai中所有边的权重和。
- 除以这个值相当于对切图每个图的cost做了均衡，避免切割过于细，导致出现一堆节点的情况。
- 这样加入分母，我们希望cut尽量小，则分母就尽量大，所以就会比第一种cut尽可能的使切割后的子图内多一些节点。
二、相似度矩阵
前面1.3中，定义了每两个节点比如节点i和节点j，之间的相似度wij，这部分就是，关于这个相似度w是如何得到的。
2.1 相似度矩阵
相似度矩阵就是样本点中的任意两个点之间的距离度量，在聚类算法中可以表示为距离近的点它们之间的相似度比较高，而距离较远的点它们的相似度比较低，甚至可以忽略。这里用三种方式表示相似度矩阵：一是ε-近邻法（ε-neighborhood graph），二是k近邻法（k-nearest nerghbor graph），三是全连接法（fully connected graph）
2.2 ε-近邻法（ε-neighborhood graph）
节点i和节点j之间，
- sij表示两点间欧氏距离的平方
- 下标i与j是节点的编号
- xi与xj是节点上的信号
推算到整个相似度矩阵即：
- 大W为相似度矩阵，小w为矩阵中的元素，表示节点间的相似度即上面1.3中w的由来
- Wij中的第i行第j列元素表示节点i与节点j的相似度wij
- sij大于阈值ε置为0，即距离太远就表示为不相邻
- sij小于阈值ε置为ε，即距离较近也表示为距离为ε
这种方法一刀切，会损失较多信息，因此很少采用。
2.3 k近邻法（k-nearest nerghbor graph）
每个样本点比如xi最近的k个点定义为KNN(xi)，k近邻法得到的W为：
或者
如果一个节点对于另一个节点属于k个最近的节点之内，则用高斯核函数得到两点之间的距离作为w
如果不在k个最临近的节点之内，则设为0
第二种不置零的条件相对第一种更加严格，即两点互为k近邻才不设为0
第一种条件相对宽松，只要一个节点对于另一个节点为k近邻就不用置零
所以第二种得到的W矩阵更容易稀疏
2.4 全连接法（fully connected graph）
径向基函数 (Radial Basis Function 简称 RBF)
直接用高斯核函数作为距离，
- 表示样本点之间的相似度w直接用高斯核函数的距离表示
- σ表示样本点的邻域宽度，σ越大则w越大，即样本点之间的相似度越大
- 可以参考右图，σ可以看做半径，σ越大则对于同一个点的高度越高即w越大，越相近
依然存在一个问题：对于同样的图，σ是否影响聚类的结果？
σ越大则对于所有样本点的相当于除以了同样的值，则之前算得的距离只是做了相同的变换，那么最终的聚类结果是否一样？
实验得出的结论是，σ变化之后，聚类结果就变了。可能因为高斯核函数是一个非线性的函数，相当于对线性的欧式距离做了一个非线性的映射，因此σ变化之后非线性映射变了，最终优化的结果也会发生改变。
指数函数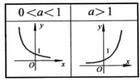
高斯核函数（径向基函数，即RBF），非线性的，所以σ变大之后w就会变大。
三、切图方法理论推导
问题描述：我们通过上面部分，把Graph Clustering转换为了一个Graph Cut的问题，然后又转换为了最小化cut的问题。
即：最好的聚类方法，就是最小化cut的时候，graph分割成的子集。
3.1 最小化Ratio Cut
我们将切图聚类问题，转换为 
即将图G切为k个子集，
，让这k个子集满足最小化
3.2 指引向量H
为了更好的解决这个问题，我们引入一个概念，指引向量H，指引向量与分割方法是等价的，每个一指引向量表示一种分割方法。这样分割图的问题又等价为求指引向量的问题。
我们引入的指示向量 
，其中j为子集的下标，与Graph切割后的每个子集对应。每个hj之中的元素为：
其中i为样本下标（节点下标），这个指示向量 hj,i 即每个子集与所有节点之间的对应关系，若节点i被分入了子集Aj之中，则hj的第i个元素为
，否则为0.整张分割之后的图的指引向量为
若想看具体推导，见：https://blog.csdn.net/yc_1993/article/details/52997074
这样定义之后，经过一系列推导，推导过于繁琐，我们只得出最后简洁的结论。
3.3 结论
推导很复杂，但是结论很简洁，只与指引向量H和拉普拉斯矩阵L有关系：
即Ratiocut的值为 
的迹，即对角线元素的和。
那么最小化Ratiocut的问题转化为求能最小化
时候的H
其中，需要对H进行标准化处理
聚类的时候，分别对H中的行进行聚类即可，通常是kmeans，也可以是GMM，具体看效果而定。
所以问题的转换是这样的：图聚类——切图——求最小化cut——求最小化cut对应的指引向量H
3.4 Ncut 同理
对于Ncut需要更改的地方就是cut计算的公式分母不一样，问题转换还是一样的，推导过程非常类似：
图聚类——切图——求最小化cut——求最小化cut对应的指引向量H——得到了分类的方法
通过上面，我们将最小化Ratiocut的问题转换为了最小化
的问题，然后对于Ncut的情况，可以直接类推一下。
类似的，指示变量为：
最终
但是再此基础上，Ncut有一定的特殊性，推导见：https://blog.csdn.net/yc_1993/article/details/52997074
，进一步转化问题：
可以对F进行标准化：
之后再对F的行进行kmeans或GMM聚类即可。
四、算法流程
https://www.cnblogs.com/pinard/p/6221564.html
上面第二部分理论推导，问题的转换是这样的：图聚类——切图——求最小化cut——求最小化cut对应的指引向量H
https://blog.csdn.net/yc_1993/article/details/52997074
我们以Ncut为例，最后一步采用k-means聚类，来讲一下算法的流程。
4.1 输入输出
输入为图G=(V,E)
输出为图聚类之后的结果，就是其聚类切割之后的k个不重不漏的子集
4.2 流程
根据输入的相似矩阵的生成方式构建样本的相似矩阵S（表明节点之间的关系，可以理解为节点间的correlation matrix甚至可以理解为adjacency matrix邻接矩阵。）
- 根据相似矩阵S构建邻接矩阵A，构建度矩阵D
- 计算出拉普拉斯矩阵L（方法见1.1）
- 构建标准化后的拉普拉斯矩阵
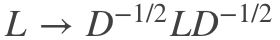
- 进行特征值分解，最小的k1个特征值所各自对应的特征向量f
- 将各自对应的特征向量f组成的矩阵按行标准化，最终组成n×k1维的特征矩阵F（这里我们不知道F是不是等价于上面的指引向量H，也不知道傅立叶变换的基与指引向量之间的关系）
- 对F中的每一行作为一个k1维的样本，共n个样本，用输入的聚类方法进行聚类，聚类维数为k2
- 根据聚类结果得到子集
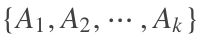
相关论文详解：
GCN (Graph Convolutional Network) 图卷积网络概览
图注意力网络(GAT) ICLR2018, Graph Attention Network论文详解
旷视CVPR2019图卷积多标签图像识别Multi-Label Image Recognition with Graph Convolutional Networks论文详解
无监督图嵌入Unsupervised graph embedding|基于对抗的图对齐adversarial graph alignment详解
Graph特征提取方法:谱聚类(Spectral Clustering)详解
参考
【博客】谱聚类（spectral clustering）原理总结
【博客】谱聚类（spectral clustering)及其实现详解
【博客】谱聚类算法(Spectral Clustering)
【Codes】pspectralclustering
【Paper】Parallel Spectral Clustering in Distributed Systems
【API】sklearn.cluster.SpectralClustering
【Demo】Comparing different clustering algorithms on toy dataset