Maxout Networks原理及源码

本篇blog内容基于Maxout Networks(Goodfellow, Yoshua Bengio, 2013)。在GAN很多应用中都用到了这个技巧。

全篇大部分转载自：Maxout Networks，

深度学习（二十三）Maxout网络学习  作者：hjimce 

---

一、Dropout

Gooddfellow在GAN本作中提到过一句话，自深度学习复苏以来，我们享受着计算资源的大幅度提升和dropout高效避免过拟合的便利，所以才有了现在这么繁荣的深度学习热。而本篇maxout在开篇便复习了一下dropout。

• dropout可以训练集成模型，它们共享参数并近似的对这些模型的预测进行了平均。它可以被当作一种通用的方法用在任何一种MLP和CNN模型中。但是在论文中，由于dropout的模型平均过程没有被证明，因而一个模型最好的性能的获得，应该通过直接设计这个模型使之可以增强dropout的模型平均的能力。使用了dropout的训练过程和一般的SGD方法完全不同。dropout在更新时使用更大的步长最有效，因为这样可以在不同的训练子集上对不同的模型有明显的影响来使得目标函数有持续的波动性，理想情况下整个训练过程就类似于使用bagging来训练集成的模型（带有参数共享的约束）。而一般的SGD更新时会使用更小的步长，来使得目标函数平滑的下降。对于深度网络模型，dropout只能作为模型平均的一种近似，显式的设计模型来最小化这种近似误差也可以提高dropout的性能。

• dropout训练的集成模型中，所有模型都只包括部分输入和部分隐层参数。对每一个训练样本，我们都会训练一个包括不同隐层参数的子模型。dropout与bagging的相同点是不同的模型使用不同数据子集，不同点是dropout的每个模型都只训练一次且所有模型共享参数。

• 对于预测时如何平均所有子模型的问题，bagging一般使用的是算数平均，而对dropout产生的指数多个子模型则并非显而易见。但是如果模型只有一层作为输出的几何平均，则最终的预测分布就是简单的，i.e. 指数多个子模型的平均预测就是完整模型的预测仅仅将权重减半而已。这个结果只能用在单softmax层的模型中，如果是深层模型如MLP，那么权重减半的方法只是几何平均的一种近似。

引用自：Maxout Networks

 

二、Maxout

1. Maxout结构

Maxout始终前向反馈的结构，就像MLP或者DeepCNN一样使用一个新型的激活函数：maxout· unit。

• 给定一个输入x，maxout的一个隐藏层遵循下面的公式：

                                                                    ​​​​​

W,b 是要学习的参数，可以看到maxout网络也属于一种非线性变换。

 

2. 理解

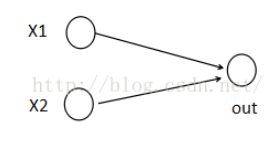
假设我们网络第i层有2个神经元x1、x2，第i+1层的神经元个数为1个，如下图所示：

(1)以前MLP的方法。我们要计算第i+1层，那个神经元的激活值的时候，传统的MLP计算公式就是：

                                                                               

                                                                                   

其中f就是我们所谓的激活函数，比如Sigmod、Relu、Tanh等。

(2)Maxout 的方法。如果我们设置maxout的参数k=5，maxout层就如下所示：

相当于在每个输出神经元前面又多了一层。这一层有5个神经元，此时maxout网络的输出计算公式为：

                                                                          

                                                                  

所以这就是为什么采用maxout的时候，参数个数成k倍增加的原因。本来我们只需要一组参数就够了，采用maxout后，就需要有k组参数。

引用自原文：深度学习（二十三）Maxout网络学习  作者：hjimce 

 

3. MLP中的Maxout

• 对MLP而言（下图），2个输入节点先构成5个“隐隐层”节点，然后在5个“隐隐层”节点中使用最大的构成了本层的一个节点，本层其他节点类似。

实现技巧：

① maxout和relu唯一的区别是，relu使用的max(x,0)是对隐层每一个单元执行的与0比较最大化操作，而maxout是对5个“隐隐层”单元的值执行最大化操作。

②如果将“隐隐层”单元在隐层展开，那么隐层就有20个“隐隐层”单元，maxout做的就是在这20个中每5个取一个最大值作为最后的隐层单元，最后的隐层单元仍然为4个。这里每5个取一个最大值也称为最大池化步长（max pooling stride）为5，最大池化步长默认和“隐隐层”个数相等，如果步长更小，则可以实现重叠最大池化。 

③实现的时候，可以将隐层单元数设置为20个，权重维度（2，20）偏置维度（1，20），然后在20个中每5个取一个最大值得到4个隐层单元。

引用自：Maxout Networks

 

4. CNN中的Maxout

• 对于CNN而言，假设上一层有2个特征图，本层有4个特征图，那么就是将输入的2个特征图用5个滤波器卷积得到5张仿射特征图（affine feature maps），然后从这5张仿射特征图每个位置上选择最大值（跨通道池化，pool across channels）构成一张本层的特征图，本层其他特征图类似。
   

实现技巧：

①relu使用的max(x,0)是对每个通道的特征图的每一个单元执行的与0比较最大化操作，而maxout是对5个通道的特征图在通道的维度上执行最大化操作。

②如果把5个特征图在本层展开，那么本层就有20个特征图，maxout做的就是在这20个中每5个取在通道维度上的最大值作为最后的特征图，最后本层特征图仍然为4个。同样最大池化步长默认为5。 

③实现的时候，可以将本层特征图数设置为20个，权重维度（20，2，3，3）偏置维度（1，20，1，1），然后在20个中每5个取一个最大特征图得到4个特征图。 

引用自：Maxout Networks

注意： 对于CNN而言，在maxout输出后如果连接一个一般的降采样最大池化层，则可以将这个降采样最大池化融合进跨通道池化中，即在仿射特征图的每个池化窗口中选择最大值（相当于同时在通道间和空间取最大值）。这样就可以在maxout网络中省略显式的降采样最大池化层。

 

三、Maxout的一些特性

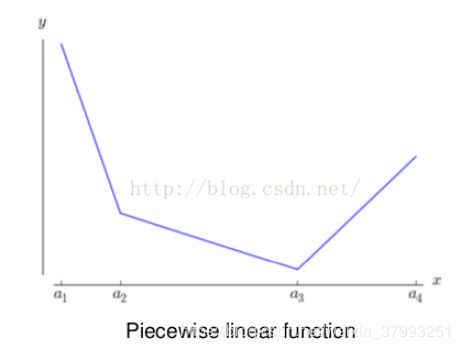
• 单个maxout激活函数可以理解成一种分段线性函数来近似任意凸函数（任意的凸函数都可由分段线性函数来拟合）。它在每处都是局部线性的（k个“隐隐层”节点都是线性的，取其最大值则为局部线性，分段的个数与k值有关），而一般的激活函数都有明显的曲率。
• 如同MLP一样，maxout网络也可以拟合任意连续函数。只要maxout单元含有任意多个“隐隐层”节点，那么只要两个隐层的maxout网络就可以实现任意连续函数的近似。
• maxout网络不仅可以学习到隐层之间的关系，还可以学习到每个隐层单元的激活函数。
• maxout放弃了传统激活函数的设计，它产生的表示不再是稀疏的，但是它的梯度是稀疏的，且dropout可以将它稀疏化。
• maxout没有上下界，所以让它在某一端饱和是零概率事件。
• 如果训练时使用dropout，则dropout操作在矩阵相乘之前，而并不对max操作的输入执行dropout。
• 使用maxout会默认一个先验：样本集是凸集可分的。

引用自：Maxout Networks

 

然而任何一个凸函数，都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数：relu、abs激活函数，看成是分成两段的线性函数，如下示意图所示：

maxout的拟合能力是非常强的，它可以拟合任意的的凸函数。最直观的解释就是任意的凸函数都可以由分段线性函数以任意精度拟合（学过高等数学应该能明白），而maxout又是取k个隐隐含层节点的最大值，这些”隐隐含层"节点也是线性的，所以在不同的取值范围下，最大值也可以看做是分段线性的（分段的个数与k值有关）-本段摘自：http://www.cnblogs.com/tornadomeet/p/3428843.html
maxout是一个函数逼近器，对于一个标准的MLP网络来说，如果隐藏层的神经元足够多，那么理论上我们是可以逼近任意的函数的。类似的，对于maxout 网络也是一个函数逼近器。

定理1：对于任意的一个连续分段线性函数g(v)，我们可以找到两个凸的分段线性函数h1(v)、h2(v)，使得这两个凸函数的差值为g(v)：
 

引用自原文：深度学习（二十三）Maxout网络学习  作者：hjimce 

http://www.cnblogs.com/tornadomeet/p/3428843.html

 

四、源码实现

项目源码网站为：https://github.com/fchollet/keras。下面是keras关于maxout网络层的实现函数：

#maxout 网络层类的定义
class MaxoutDense(Layer):
    # 网络输入数据矩阵大小为(nb_samples, input_dim)
    # 网络输出数据矩阵大小为(nb_samples, output_dim)
    input_ndim = 2
   #nb_feature就是我们前面说的k的个数了，这个是maxout层特有的参数
    def __init__(self, output_dim, nb_feature=4,
                 init='glorot_uniform', weights=None,
                 W_regularizer=None, b_regularizer=None, activity_regularizer=None,
                 W_constraint=None, b_constraint=None, input_dim=None, **kwargs):
        self.output_dim = output_dim
        self.nb_feature = nb_feature
        self.init = initializations.get(init)
 
        self.W_regularizer = regularizers.get(W_regularizer)
        self.b_regularizer = regularizers.get(b_regularizer)
        self.activity_regularizer = regularizers.get(activity_regularizer)
 
        self.W_constraint = constraints.get(W_constraint)
        self.b_constraint = constraints.get(b_constraint)
        self.constraints = [self.W_constraint, self.b_constraint]
 
        self.initial_weights = weights
        self.input_dim = input_dim
        if self.input_dim:
            kwargs['input_shape'] = (self.input_dim,)
        self.input = K.placeholder(ndim=2)
        super(MaxoutDense, self).__init__(**kwargs)
    #参数初始化部分
    def build(self):
        input_dim = self.input_shape[1]
 
        self.W = self.init((self.nb_feature, input_dim, self.output_dim))#nb_feature是我们上面说的k。
        self.b = K.zeros((self.nb_feature, self.output_dim))
 
        self.params = [self.W, self.b]
        self.regularizers = []
 
        if self.W_regularizer:
            self.W_regularizer.set_param(self.W)
            self.regularizers.append(self.W_regularizer)
 
        if self.b_regularizer:
            self.b_regularizer.set_param(self.b)
            self.regularizers.append(self.b_regularizer)
 
        if self.activity_regularizer:
            self.activity_regularizer.set_layer(self)
            self.regularizers.append(self.activity_regularizer)
 
        if self.initial_weights is not None:
            self.set_weights(self.initial_weights)
            del self.initial_weights
 
    def get_output(self, train=False):
        X = self.get_input(train)#需要切记这个x的大小是(nsamples,input_num) 
        # -- don't need activation since it's just linear.
        output = K.max(K.dot(X, self.W) + self.b, axis=1)#maxout激活函数
        return output

看上面的代码的话，其实只需要看get_output()函数，就知道maxout的实现了。所以说有的时候，一篇文献的代码，其实就只有几行代码，maxout就仅仅只有一行代码而已：

output = K.max(K.dot(X, self.W) + self.b, axis=1)#maxout激活函数

 

五、 测试结果

1. MNIST

• 排列不变限制的MNIST（MNIST with permutation invariant，即像素排列顺序可以改变，输入的数据是2维的），使用两个全连接maxout层再接上一个sorfmax层，结合dropout和权重衰减。验证集选取训练集中后10000个样本。在得到最小的验证集误差时记录下前50000个样本的训练集对数似然LL，接着在整个60000样本的训练集上继续训练直到验证集的对数似然达到LL。0.94%
• 无排列不变限制的MNIST（MNIST without permutation invariant，即像素排列顺序不变，输入的数据是3维的），使用三个卷积maxout层，之后接上空间最大池化层，最后接上一个softmax层。还可以使用扩充数据集的方法进一步提高。0.45%

2. CIFAR-10

• 预处理：全局像素归一化和ZCA白化
• 过程与MNIST类似，只是将继续训练改为了重新训练，因为继续训练的学习率很低训练太久。
• 使用三个卷积maxout层，之后接上全连接maxout层，最后接上一个softmax层。13.2%（不使用验证集数据）11.68%（使用验证集数据）9.35%（使用平移、水平翻转的扩充数据集）

3. CIFAR-100

• 超参数使用和CIFAR-10一样
• 41.48%（不使用验证集数据）38.57%（使用验证集数据）

4. SVHN

• 验证集为训练集每类选取400个样本和额外集每类选取200个样本，其他的为训练集。
• 预处理：局部像素归一化
• 使用三个卷积maxout层，之后接上全连接maxout层，最后接上一个softmax层（同CIFAR-10）。2.47%

 

六、maxout对比relu

• 跨通道池化可以减少网络状态并减少模型所需要的参数。
• 对于maxout，性能与跨通道池化时滤波器数量有很大关系，但对relu，性能与输出单元的数量没有关系，也就是relu并不从跨通道池化中受益。
• 要让relu达到maxout的表现，需要使之具有和maxout相同数量的滤波器（即使用比原来kk倍的滤波器，同样也要k倍的relu单元），但网络状态和所需要的参数也是原来的kk倍，也是对应maxout的kk倍。

 

七、 模型平均

• 单层softmax有对模型进行平均的能力，但是通过观察，多层模型中使用dropout也存在这样的模型平均，只是有拟合精度的问题。
• 训练中使用dropout使得maxout单元有了更大的输入附近的线性区域，因为每个子模型都要预测输出，每个maxout单元就要学习输出相同的预测而不管哪些输入被丢弃。改变dropout mask将经常明显移动有效输入，从而决定了输入被映射到分段线性函数的哪一段。使用dropout训练的maxout具有一种特性，即当dropout mask改变时每个maxout单元的最大化滤波器相对很少变化。
• maxout网络中的线性和最大化操作可以让dropout的拟合模型平均的精度很高。而一般的激活函数几乎处处都是弯曲的，因而dropout的拟合模型平均的精度不高。

 

八、 优化

• 训练中使用dropout时，maxout的优化性能比relu+max pooling好
• dropout使用更大的步长最有效，使得目标函数有持续的波动性。而一般的SGD会使用更小的步长，来使得目标函数平滑的下降。dropout快速的探索着许多不同的方向然后拒绝那些损害性能的方向，而SGD缓慢而平稳的朝向最可能的方向移动。
• 实验中SGD使得relu饱和在0值的时间少于5%，而dropout则超过60%。由于relu激活函数中的0值是一个常数，这就会阻止梯度在这些单元上传播（无论正向还是反向），这也就使得这些单元很难再次激活，这会导致很多单元由激活转变为非激活。而maxout就不会存在这样的问题，梯度在maxout单元上总是能够传播，即使maxout出现了0值，但是这些0值是参数的函数可以被改变，从而maxout单元总是激活的。单元中较高比例的且不易改变的0值会损害优化性能。
• dropout要求梯度随着dropout mask的改变而明显改变，而一旦梯度几乎不随着dropout mask的改变而改变时，dropout就简化成为了SGD。relu网络的低层部分会有梯度衰减的问题（梯度的方差在高层较大而反向传播到低层后较小）。maxout更好的将变化的信息反向传播到低层并帮助dropout以类似bagging的方式训练低层参数。relu则由于饱和使得梯度损失，导致dropout在低层的训练类似于一般的SGD。

 

引用自：Maxout Networks

引用自原文：深度学习（二十三）Maxout网络学习  作者：hjimce