这一小节,总结一下排序算法和搜索相关的知识
一、排序算法
在学习的过程中,发现了下面这个可交互的网站,做的非常的不错,强力推荐大家去看看这个网站。
Problem Solving with Algorithms and Data Structures using Python
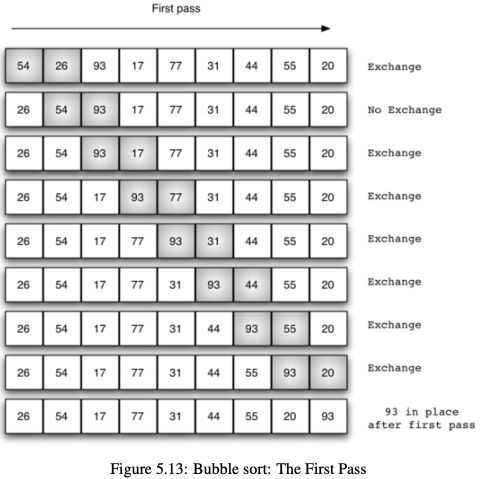
1、冒泡排序
思想:
对于含有n个元素的数组来说
- 相邻的两个元素比较,如果前面一个元素比后面一个元素大,那么就交换他们两个。我们需要遍历一下数组,第一个元素开始,那么需要比较n-1次,那么最大的元素就到了最后的位置。针对第二个元素,那么需要n-2次比较,第二大的元素就到了最后的位置。重复这个过程,我们可以得到下面的一个表:
| 遍历的第几个元素 | 比较次数 |
|---|---|
| 1 | n-1 |
| 2 | n-2 |
| 3 | n-3 |
| ... | ... |
| n-1 | 1 |
-
所以有这个原理之后,可以和水里面的冒泡的过程给类比过来
下面就代码实现以下把
def BubbleSort(alist):
n = len(alist)
for i in range(1, n+1):
for j in range(n-i):
if alist[j] >=alist[j+1]:
alist[j], alist[j+1] = alist[j+1], alist[j]
return alist
针对时间复杂度而言:
最优时间复杂度:O(n) (表示的就是比例依次发现没有元素可以交换)
最坏时间复杂度:O(n^2)
稳定性:稳定
优化代码
def BubbleSort(alist):
n = len(alist)
for i in range(1, n+1):
count = 0
for j in range(n-i):
if alist[j] >=alist[j+1]:
alist[j], alist[j+1] = alist[j+1], alist[j]
count+=1
if count ==0:
return
return alist
2、选择排序
思路:
选择排序的思路还是挺直观的。在未排序的序列里面找到最小元素,将其放到排序序列的起始位置,然后再从未排序的序列中继续查找最小元素,将其放到已排序元素的末尾。重复这个过程
def SelectionSort(alist):
n = len(alist)
for i in range(n-1):
min_pos = i
for j in range(i+1, n-1):
if alist[min_pos] >=alist[j+1]:
alist[min_pos], alist[j+1] = alist[j+1], alist[min_pos]
min_pos = j+1
return alist
最优时间复杂度:O(n^2)
最坏时间复杂度:O(n^2)
稳定性:不稳定
3、插入排序
思路:在进行插入排序的时候,我们可以把数组看成两个部分,前面一个部分是已经排好序的部分,然后后面一部分是没有排序好的部分,那么我们就从没有排序好的序列中的元素第一个元素找到合适的位置插入进去。
代码
def insertionSort1(arr):
length = len(arr)
for i in range(1,length):
for j in range(i,0,-1):
if arr[j]上述的代码中,可以提前终止内层的循环是插入排序非常重要的一个性质。但是存在了很多的的交换操作,所以使得该算法的执行的效率是不高的。所以我们进行一个代码的优化操作。
优化后的代码:优化的思想是,我们先将未排序的部分的第一个元素拿出来,和前面排序的元素比较,要是前面的元素比它大,那么就将前一个元素的值赋给后面的一个元素,知道我们找到一个位置的元素比未排序部分的第一个元素小,此时赋值给它就行了。
def insertionSort2(arr):
length = len(arr)
for i in range(1, length):
e = arr[i]
j = 0
for j in range(i,0,-1):
if arr[j-1]>e:
arr[j] = arr[j-1]
else:
break
arr[j] = e
return arr
时间复杂度:O(n^2)
空间复杂度:O(1)
4、归并排序
归并排序算法的本质还是利用到了递归的手段。假设我们有n个元素,那么我们分组的时候,就能够分出logn个层级出来。然后对每一层做一个排序的处理,那么整体下来,时间复杂度就是nlogn了。
思路一:自顶向下去解决问题
思路二:自底向上去解决问题
好了,到这里,我们的归并排序就看完了。
5、快速排序
快速排序算得上是21世纪对世界影响最大的排序算法了。而且也是在长期的改进和优化中。
思路一:单路快排,这种思路一般都是取第一个元素作为基点(假设它是6),然后我们想做的事就是将这个元素放到它正确的位置上,那么6之前的元素就是小于6的,6之后的元素就是大于6的。如何将这个元素给放到正确的位置上就是一个子过程,也是快速排序的核心所在,这个过程,我们就叫做了partition。
def __partition(arr,l,r):
v = arr[l]
j=l
for i in range(l,r+1):
if arr[i]=r:
return
p = __partition(arr, l, r)
__quickSort(arr,l,p-1)
__quickSort(arr,p+1,r)
def quickSort(arr):
__quickSort(arr,0,len(arr)-1)
return arr
但是这种写法还是有点问题的,针对有序数组的话,那么时间复杂度就很可能退化到了O(n^2)了。
思路二:两路快排
思路三:三路快排
def __quickSort3Ways(arr, l, r):
if l>=r: # 这里的一步可以优化r-l<=某个数的时候,选择插入排序
return
v = arr[l]
lt = l # arr[l+1, ... lt] 都是小于v的
gt = r+1 # arr[gt,...,r+1]这部分的元素都是大于v
i = l+1 #arr[lt+1, ..., i]这部分的元素都是等于v的
while iv:
arr[i], arr[gt-1] = arr[gt-1], arr[i]
gt-=1
else:
i+=1
arr[l], arr[lt] = arr[lt], arr[l]
__quickSort3Ways(arr, l, lt-1)
__quickSort3Ways(arr, gt, r)
def quickSort3Ways(arr):
n = len(arr)
__quickSort3Ways(arr,0,n-1)
return arr
到这里,我们的快速排序就到这里了。
6、堆排序
堆排序和树还是分不开的。
思路:
二、时间复杂度和空间复杂度的一个总结
| 排序算法 | 平均时间复杂度 | 最优时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 希尔排序 | O(n^2) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
持续更新中...
数据结构与算法系列博客:
一、数据结构与算法概述
二、数组及LeetCode典型题目分析
三、链表(Linked list)以及LeetCode题
四、栈与队列(Stack and Queue
五、树(Trees)
六、递归与回溯算法
七、动态规划
八、排序与搜索
九、哈希表
排序算法的一个总结如下:
参考资料:
1、https://www.cs.auckland.ac.nz/compsci105s1c/resources/ProblemSolvingwithAlgorithmsandDataStructures.pdf
2、http://interactivepython.org/runestone/static/pythonds/index.html