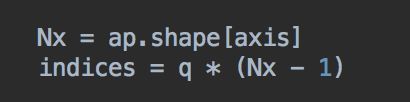数据分析EPHS(4)-使用Excel和Python计算数列统计值

前面环境都搞的差不多了，这次咱们进入实战篇，来计算一列的统计值。统计值主要有最大值、最小值、均值、标准差、中位数、四分位数。话不多说，直接进入正题。

本文介绍使用Excel和Python来计算上述统计值，而Hive和Spark将放在下一篇中。

1、数据介绍

这里咱们使用的是iris分类数据集，数据下载地址为：

http://archive.ics.uci.edu/ml/datasets/Iris

下载后转换为xlsx格式的文件，数据如下：

也可以在公众号后台回复 “iris” 下载相应数据。

2、使用Excel计算统计值

咱们一个个来哈，在使用过程中还是学到了很多东西的，如果你都会了，也建议你看一下，嘻嘻！

2.1 最大值 & 最小值

在Excel统计一列或者指定单元格区间的最大值或最小值，直接使用max和min函数即可：

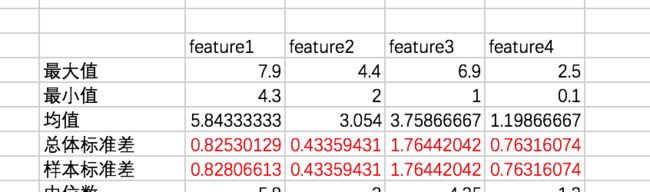
=MAX(A2:A151)=MIN(A2:A151)

统计结果如下：

2.2 平均值

在Excel统计一列或者指定单元格区间的平均值，直接使用average函数即可：

=AVERAGE(A2:A151)

统计结果如下：

2.3 样本标准差 VS 总体标准差

在Excel统计一列或者指定单元格区间的标准差，可就没那么简单了，excel里面共有四个方法：

共四个方法，其实可以分成两组，即统计样本标准差和总体标准差，首先回顾一下二者的计算公式：

总体标准差对应的英文是Population standard deviation , 在Excel中一般使用STDEV.P 或者 STDEVPA方法计算，这里的P便是Population的意思。
样本标准差对应的英文是Sample standard deviation，在Excel中一般使用STDEV.S 或者 STDEVA方法计算，这里的S便是Sample的意思。

这里我们先使用STDEV.P和STDEV.S 分别计算一下总体标准差和样本标准差：

=STDEV.P(A2:A151)=STDEV.S(A2:A151)

结果如下：

接下来说下STDEV.P和 STDEVPA的区别，STDEV.S和STDEVA的区别与其相同。两者区别是 STDEV.P 函数忽略样本中的逻辑值和文本, STDEVPA 不忽略，看下面的结果：

在上面的数据中，如果只计算4个数字的总体标准差，结果当然是0，因为四个数字都是2，所以STDEV.P的结果是0，但是STDEVPA的结果却不是0，因为这个函数将文本和逻辑值False当作0处理，把逻辑值True当作1处理，我们来验证下：

结果印证了咱们刚才的说明。

2.3 中位数

在Excel统计一列或者指定单元格区间的中位数，直接使用MEDIAN函数即可：

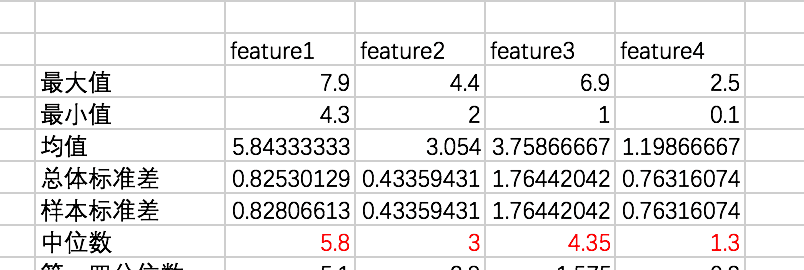
=MEDIAN(A2:A151)

中位数的计算方法，如果数据量的个数为奇数的话，就是中间的一个数，如果数据量个数为偶数个的话，就是最中间两个数的平均值，咱们这里是150个数，所以是排序后第75个数和76个数的平均值，如feature3，两个数分别是4.3和4.4，所以中位数是4.35：

2.4 四分位数

这里，四分位数计算又有两种方法了：

其中QUARTILE.EXC对应了n+1的方法，QUARTILE.INC对应了n-1的方法。咱们先介绍下计算四分位数的n+1和n-1方法：

对于n+1方法，如果数据量为n，则四分位数的位置为：

Q1的位置= (n+1) × 0.25
Q2的位置= (n+1) × 0.5
Q3的位置= (n+1) × 0.75

对于n-1方法，如果数据量为n，则四分位数的位置为：

Q1的位置=1+（n-1）x 0.25
Q2的位置=1+（n-1）x 0.5
Q3的位置=1+（n-1）x 0.75

可以看到，两种方法计算的Q2的结果是相同的，且与中位数的结果相同。但是Q1和Q3的结果却不相同。如在我们的数据中的feature3。若使用n+1方法，那么Q1的位置为151 * 0.25 = 37.75，如果使用n-1方法，那么Q1的位置为1 + 149 * 0.25 = 38.25。在数据中，第37、38、39个数分别为1.5、1.6、1.6。因此使用n+1方法得到的Q1 = 1.5 * 0.25 + 1.6 * 0.75 = 1.575，而使用n-1方法得到的Q1 = 1.6 * 0.75 + 1.6 * 0.25 = 1.6。

继续说，无论QUARTILE.EXC还是QUARTILE.INC方法，都需要两个两个参数，第一个是指定的单元格区间，第二个是求第几四分位数，如下面是求第一四分位数：

=QUARTILE.INC(A2:A151,1)

最终的结果如下：

好了，EXCEL部分的说明先到这里了，接下来用Python来计算一下。

3、使用Python计算统计值

使用Python的话，咱们分为四个方面来介绍，即使用list、numpy和pandas来计算数列的统计值。

3.1 计算List的统计值

这里，我们对原始的list进行操作，除了max和min有现成的方法之外，其余各个统计值的计算，要按照对应的公式进行计算，代码如下：

irisdf = pd.read_csv('data/iris.csv')feature1list = irisdf['feature1'].values.tolist()max_value_list = max(feature1list)min_value_list = min(feature1list)avg_value_list = sum(feature1list) / len(feature1list)std_value_list = math.sqrt(sum([math.pow(x - avg_value_list,2) for x in feature1list])/len(feature1list))feature1list = sorted(feature1list)number_cnt = len(feature1list)if number_cnt % 2 == 1:    median_value_list = feature1list[(number_cnt-1) // 2]else:    median_value_list = (feature1list[number_cnt//2] + feature1list[number_cnt // 2-1]) / 2q1_pos = (number_cnt + 1) * 0.25q2_pos = (number_cnt + 1) * 0.5q3_pos = (number_cnt + 1) * 0.75q1_value_list = feature1list[int(q1_pos) -1] * (1 - q1_pos % 1) + feature1list[int(q1_pos)] * (q1_pos % 1)q2_value_list = feature1list[int(q2_pos) -1] * (1 - q2_pos % 1) + feature1list[int(q2_pos)] * (q2_pos % 1)q3_value_list = feature1list[int(q3_pos) -1] * (1 - q3_pos % 1) + feature1list[int(q3_pos)] * (q3_pos % 1)print("最大值是：" + str(max_value_list))print("最小值是：" + str(min_value_list))print("平均值是：" + str(avg_value_list))print("总体标准差是：" + str(std_value_list))print("中位数是：" + str(median_value_list))print("第一四分位数是：" + str(q1_value_list))print("第二四分位数是：" + str(q2_value_list))print("第三四分位数是：" + str(q3_value_list))

输出的结果为：

最大值是：7.9最小值是：4.3平均值是：5.843333333333335总体标准差是：0.8253012917851409中位数是：5.8第一四分位数是：5.1第二四分位数是：5.8第三四分位数是：6.4

和excel保持一致。

3.2 使用Numpy计算统计值

使用numpy的话，每个都有对应的函数，咱们直接看看代码，后面会对代码做一些说明：

feature1array = np.array(feature1list)max_value_array = feature1array.max()min_value_array = feature1array.min()avg_value_array = feature1array.mean()std_value_array = feature1array.std(ddof = 0)sstd_value_array = feature1array.std(ddof = 1)median_value_array = np.median(feature1array)q1_value_array = np.percentile(feature1array,25)q2_value_array = np.percentile(feature1array,50)q3_value_array = np.percentile(feature1array,75)print("最大值是：" + str(max_value_array))print("最小值是：" + str(min_value_array))print("平均值是：" + str(avg_value_array))print("总体标准差是：" + str(std_value_array))print("样本标准差是：" + str(sstd_value_array))print("中位数是：" + str(median_value_array))print("第一四分位数是：" + str(q1_value_array))print("第二四分位数是：" + str(q2_value_array))print("第三四分位数是：" + str(q3_value_array))

结果输出为：

最大值是：7.9最小值是：4.3平均值是：5.84333333333总体标准差是：0.825301291785样本标准差是：0.828066127978中位数是：5.8第一四分位数是：5.1第二四分位数是：5.8第三四分位数是：6.4

这里，我们主要对标准差计算和四分位数计算作出说明，对于标准差，使用的是std方法：

std_value_array = feature1array.std(ddof = 0)sstd_value_array = feature1array.std(ddof = 1)

可以看到，我们指定了一个参数ddof，这里ddof=0代表计算总计标准差，ddof=1代表计算样本标准差，默认ddof=0。

计算四分位数使用的是np.percentile方法：

q1_value_array = np.percentile(feature1array,25)q2_value_array = np.percentile(feature1array,50)q3_value_array = np.percentile(feature1array,75)

首先，第二个参数是整数，而非0.25或者0.5。其次，四分位索引的计算基于我们说的n-1计算方法，可以看下源码中相应的部分：

3.3 使用Pandas计算统计值

使用pandas的话，直接通过describe方法就可以输出我们本文所介绍的一堆统计值：

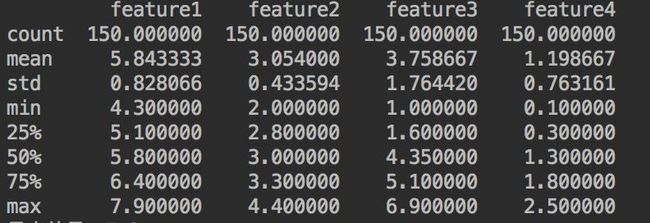
irisdf_describe = irisdf.describe()print(irisdf_describe)

输出为：

这里已经有最大值、最小值、平均值、四分位数等数据，而这里的标准差是样本标准差，所以我们还需要统计中位数和总体标准差：

irisdf_describe = irisdf.describe()print(irisdf_describe)median_value_df = irisdf['feature1'].median()std_value_df = irisdf['feature1'].std(ddof=0)print("最大值是：" + str(irisdf_describe['feature1']['max']))print("最小值是：" + str(irisdf_describe['feature1']['min']))print("平均值是：" + str(irisdf_describe['feature1']['mean']))print("总体标准差是：" + str(std_value_df))print("样本标准差是：" + str(irisdf_describe['feature1']['std']))print("中位数是：" + str(median_value_df))print("第一四分位数是：" + str(irisdf_describe['feature1']['25%']))print("第二四分位数是：" + str(irisdf_describe['feature1']['50%']))print("第三四分位数是：" + str(irisdf_describe['feature1']['75%']))

结果为：

最大值是：7.9最小值是：4.3平均值是：5.84333333333总体标准差是：0.825301291785样本标准差是：0.828066127978中位数是：5.8第一四分位数是：5.1第二四分位数是：5.8第三四分位数是：6.4

好了，今天的介绍就到这里了，总体来说看似很简单，但还是有很多学问在里面的，好好学习一下吧。