『为金融数据打标签』「1. 三隔栏方法」

本文有 3816 字，22 图表截屏

建议阅读 20 分钟

休假中，硬着写一篇出来。

0

引言

本文是 AFML 系列的第四篇

1. 金融数据类型

2. 从 Tick 到 Bar

3. 特征抽样

4. 三隔栏方法

众所周知，在用有监督学习算法对未来的金融产品收益情况进行预测时，需要从训练集中拟合一个模型，而第一步需要对训练集里每个样本打标签，即为每个 X⁽ⁱ⁾ 标注一个 y⁽ⁱ⁾，其中 i = 1, 2, ..., n。

本帖介绍两种方法：

1. 固定时间区间方法（经典）

2. 三隔栏方法（实际）

本帖里用的数据来自〖数据结构之 Pandas (下)〗6.1 小节，公众号回复 data 可以下载。

下面我们用苹果（代号 AAPL）一年的股票数据举例。

1

固定时间区间方法

几乎所有机器学习文献都使用了固定时间区间（Fixed-time Horizon, FH）方法对金融数据打标签。

这种方法简单直观，判断规则十分简单。在固定时间内对于某个股票，如果其收益

• 高于阈值 c，那么被分为正例 (用 +1 表示)

• 低于阈值 -c，那么被分为负例 (用 -1 表示)

• 在 -c 和 c 之间，被分为第三类 (用 0 表示)

用公式对上述规则进行表述。

其中

• r(t_i,0, t_i,0+h) 是在固定区间 h 中的价格收益

• t_i,0 是 X⁽ⁱ⁾ 对应的 Bar 的索引

• t_i,0 +h 是在 t_i,0 后 h 个 Bar 的索引

• h 是一段固定区间

• c 是一个预先设定的收益阈值

举个实际例子，从 2019 年 1 月 27 日开盘时点（t_i,0）开始计算苹果股票10 个 bar 后（h = 10）的收益，得到 r = 0.5%，如果阈值是 0.1%（c = 0.1%），那么打上「涨」的标签。

该方法很常用，但也存在以下两个问题：

1. 在〖从 Tick 到 Bar〗一帖可知等时抽样的 Time Bar 的统计特征不好

2. 阈值 c 一直不变，但价格波动率却随时间变化，这就造成了

   1. 在波动率很大时，价格很容易突破 [-c, c]，因此很少样本会被标注为 0，大量 ±1

   2. 而波动率很小时，价格不容易突破 [-c, c]，因此很多样本会被标注为 0，少量 ±1

对于上面二个问题，也有两个解决方法：

1. 将「等时抽样的 Time Bar」换成「等量抽样的 Volume Bar 」和「等额抽样的 Dollar Bar」，因为 Volume Bar 和 Dollar Bar 两个显示的波动率比较稳定。

2. 用指数加权移动平均（Exponential-Weighted Moving Average，EWMA）在收益的时间序列上计算出波动率，做为动态阈值（dynamic threshold）的基干（backbone）。

下面代码展示如何计算日波动率。

代码不能更简单。函数接收两个参数，第 1 个 df 是 DataFrame，第 2 个是 span0指数加权平均窗口的天数。

第 2 行计算日收益，函数 shift(1) 就是把序列所有元素的索引往后移动了 1 位，第一位用 NaN 替代。

第 3 行用 Pandas 里面的 ewm() 函数，计算完指数加权平均序列的标准差作为波动率。

---

看看结果。

vol = getDailyVol( data )	
vol.head(3).append(vol.tail(3))

0     NaN
1     NaN
2     0.001221
249   0.023158
250   0.022948
251   0.022718
Name: Return, dtype: float64

前两个都是 NaN，正常。

第一个 NaN 是因为 shift(1)。第二个 NaN 是因为不能在 1 个数据上计算 std()。

计算完波动率，我们可以设定上下阈值 c_u 和 c_d

    c_u = α_u × σ

    c_d = -α_d × σ

其中 α_u 和 α_d 是缩放因子。

---

现在，即便用了 Volume Bar 或 Dollar Bar，即便计算了 EMA 波动率作为动态阈值，但是在实际交易通常会有止损（stop-loss），有时也会有止盈（profit-taking）。

下节就来探讨如何利用止损止盈来给资产涨跌打标签的。

2

三隔栏方法

AFML 作者 Prado 一种创新的数据标注方法，三隔栏（Triple-Barrier, TB）方法。这是一种路径依赖（path dependent）的标注方法，因而能够有效地解决上节提到的止损止盈问题。

「三隔栏」灵魂三问

为什么要设定三隔栏？

TB 和 FH 方法相似，我们需要三种情况来为数据打上 +1, -1, 0 三个标签，而打哪个标签看价格函数先碰到三隔栏的哪一个。

如何设定三隔栏？

设立两个价格上水平（horizontal）的隔栏和一个时间上垂直（vertical）的隔栏，其中

• 水平隔栏考虑到止损止盈，可用历史波动率的函数来定义

• 垂直隔栏考虑到时间期限，可用一定数量的 Bars 来定义

如何用三隔栏打标签？

如果

1. 上水平隔栏先被触及，将样本标注为 1

2. 下水平隔栏先被触及，将样本标注为 -1

3. 如果垂直隔栏先被触及，将样本标注为 0，或者是该时段内收益的符号，sign(r(t_i,0, t_i,0+h))

这显然是一个路径依赖的方法，因为我们需要确定在整个时间区间内三个隔栏是否在某一刻被触及。

我们定义

• t_i,1 = 第一次触碰隔栏的时点

• r(t_i,0, t_i,1) = 从开始到第一次碰隔栏时段内的收益

通常我们有 t_i,1 ≤ t_i,0+ h 关系

• 当第一次碰到竖直隔栏，用等号 =

• 当第一次碰到水平隔栏，用小于号 <

竖直隔栏

我们设定 h 为 15 天，用 events 来储存竖直隔栏对应的日期和日波动率。

第一行初始化 events，将 data 里面的 'Date' 一栏的复制给它。

第二行用 TimeDelta(days=15) 函数，加在初始日期得到竖直隔栏对应的日期。

第三行用之前定义好的函数 getDailyVol() 来计算日波动率。

水平隔栏

该函数为了计算上下水平隔栏对应的日期，用 result 来储存。

第 5 - 9 行计算上下水平隔栏的点位（level），用上述公式

    c_u = α_u × σ

    c_d = -α_d × σ

其中 σ 是日波动率。而 width = [α_u, α_d]，它们都大于等于 0

• 当大于 0 时，乘上 σ 得到水平隔栏的点位，存储在 'UB' 和 'DB' 栏下。

• 当等于 0 时，表明不设定隔栏，那么隔栏的点位就设定为 NaN

第 12 - 13 行代码在每一个窗口都运行，即每一个起始日到它 15 天之后的竖直隔栏对应的日期，计算每天的收益率。

第 16 - 17 行检查每天的收益是否突破隔栏，突破了则记录第一次突破的时点，并储存起来，'ut' 代表第一次突破上隔栏日期，'dt' 代表第一次突破下隔栏日期。

用 TBL 函数来确定三隔栏中的哪一个隔栏被突破了。下面代码第 3 行做的就是这件事，在 'VB', 'ut' 和 'dt' 栏下的日期中找出最小值（把 NaN 当做无限大），

result = get_first_touch( data, 	
                          events,	
                          width )	
result.head().append(result.tail())

八种情况

前面的 TBL() 函数的输出 result 包含碰到每个隔栏的时间戳。值为 NaT 代表该隔栏没有被突破过。

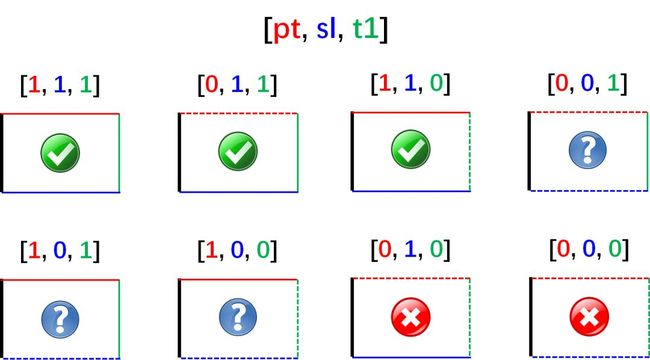
此外，我们还可以用 [pt, sl, t1] 来代表隔栏有效状态，其中

• pt 是 profit-taking 的缩写，水平隔栏

• sl 是 stop-loss 的缩写，水平隔栏

• t1 是竖直隔栏

这三个状态只能去 0 和 1，0 代表此隔栏无效，1 代表此隔栏有效。三个状态那么可能会有 8 种情况，它们分别是：

三种实际的情况（上图绿 √）：

• [1, 1, 1]：标准设置。我们希望实现盈利，但对损失和持有期限有最大限度。

• [0, 1, 1]：我们不会止盈，要么止损退出，要么过了持有期限退出。

• [1, 1, 0]：我们只会因为止盈或止损才会退出。

三种不太实际的情况（上图蓝 ?）：

• [0, 0, 1]：等价于固定时间区间方法。

• [1, 0, 1]：我们持有头寸直至获利或超过最长持有期，但不考虑止损。

• [1, 0, 0]：持仓直至获利，但也意味着多年来一直亏损。

两种不合逻辑的情况（上图红 ×）：

• [0, 1, 0]：毫无目的的配置。我们直到亏损才停止。

• [0, 0, 0]：该配置没有隔栏。永远不退出也不会生成任何标签。

下面三图分别展示了 [1, 1, 1] 标配的三种退出方式。

一. 先碰到「下水平隔栏」而止损退出。

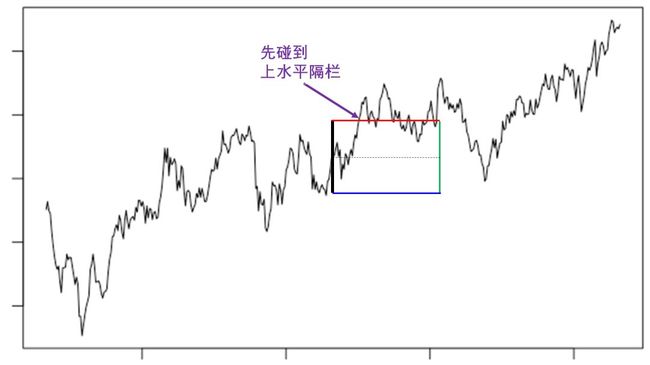
二. 先碰到「上水平隔栏」而止盈退出。

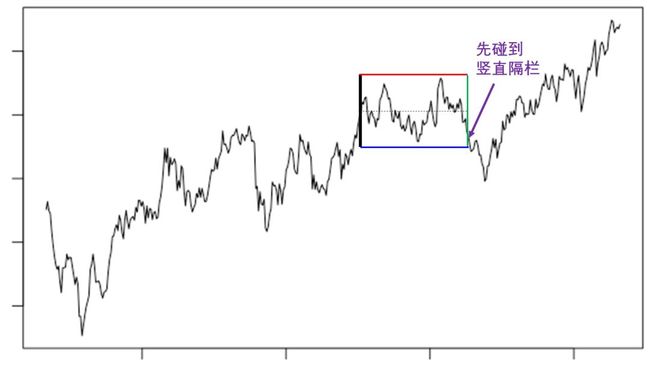
三. 先碰到「竖直隔栏」而超过持有期限退出。

打标签

该函数计算出根据每个窗口的收益正负带标住 +1 或者 -1。

第 5 行计算出起始价格。第 6 行计算出终止价格。

• 当持仓期限过了，那么终止价格就是竖直隔栏那点的价格

• 当收益碰到了上下隔栏，那么终止价格就是上下水平隔栏那点的价格

第 7 行计算收益率，第 8 行根据其正负标注 ± 1。

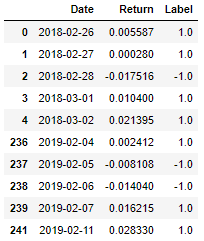
out = get_label( data, result )	
out.head().append(out.tail())

3

总结

和传统的固定时间区间方法相比，用三隔栏方法打标签考虑了

• 持仓期限（竖直隔栏）

• 止损（下水平隔栏）

• 止盈（上水平隔栏）

但实际上如果考虑做空的话，止损对应的是上水平隔栏，而止盈对应的是下水平隔栏。另外

• 除了标注头寸方向（side），还需要知道头寸大小（size）吗？

• 头寸方向如果预测错误了，情况 1 和情况 2 哪种更严重？

  • 情况 1 - 预测涨而做多，但是跌了亏钱；或预测跌而做空，但是涨了亏钱（False Positive）

  • 情况 2- 预测不涨不跌没有交易，但实际涨了或跌了而没有赚到钱 （False Negative） 

显然 False Positive 更严重些。下帖讲这些。

---

写了几篇之后，现在总觉得 Prado 有点喜欢 show-off 的感觉，一个简单的东西讲得很晦涩，一篇简单的代码写得很复杂。不知道是自己段位不够，还是本来就是这样子的。

最后，从本贴的代码可看出 Pandas 的重要性了吧。那就再次安利一下自己的 Python 盘一盘系列（点击下图）。

Stay Tuned！

王的机器

机器学习、金融工程、量化投资的干货营；快乐硬核的终生学习者。