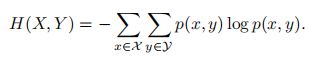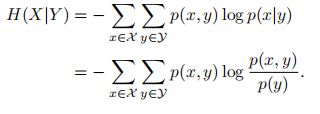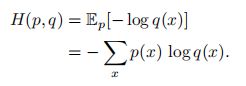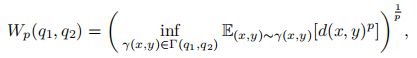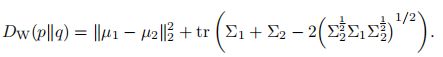前言 机器学习中的数学归纳整理（信息论部分）

本文收录归纳了一些机器学习中涉及到信息论的部分，主要用于特征抽取、统计推断、自然语言处理等。

目录

1.熵

1.1 自信息和熵

1.2 联合熵和条件熵

2.互信息

3.交叉熵和散度

3.1 交叉熵

3.2 KL 散度

3.3 JS 散度

3.4 Wasserstein 距离

---

1.熵

1.1 自信息和熵

熵（Entropy）最早是物理学的概念，用于表示一个热力学系统的无序程度。在信息论中，熵用来衡量一个随机事件的不确定性。假设对一个随机变量X（取值集合为X，概率分布为p(x), x ∈ X）进行编码，自信息I(x)是变量X = x时的信息量或编码长度，定义为：

                                 

那么随机变量X 的平均编码长度，即熵定义为：

                                

其中当p(xi) = 0时，我们定义0 log 0 = 0，这与极限一致，

熵是一个随机变量的平均编码长度，即自信息的数学期望。熵越高，则随机变量的信息越多；熵越低，则信息越少。如果变量X 当且仅当在x时p(x) = 1，则熵为0。也就是说，对于一个确定的信息，其熵为0，信息量也为0。如果其概率分布为一个均匀分布，则熵最大。

1.2 联合熵和条件熵

对于两个离散随机变量X 和Y ，假设X 取值集合为X；Y 取值集合为Y，其联合概率分布满足为p(x, y)，则X 和Y 的联合熵为：

                                      

X 和Y 的条件熵为：

                                     

根据其定义，条件熵也可以写为：

                                     

2.互信息

互信息是衡量已知一个变量时，另一个变量不确定性的减少程度。两个离散随机变量X 和Y 的互信息定义为：

                                          

互信息的一个性质为：

                                       

如果X 和Y 相互独立，即X 不对Y 提供任何信息，反之亦然，因此它们的互信息为零。

3.交叉熵和散度

3.1 交叉熵

对应分布为p(x)的随机变量，熵H(p)表示其最优编码长度。交叉熵是按照概率分布q 的最优编码对真实分布为p的信息进行编码的长度，定义为：

                                         

在给定p的情况下，如果q 和p越接近，交叉熵越小；如果q 和p越远，交叉熵就越大。

3.2 KL 散度

KL散度，也叫KL距离或相对熵，是用概率分布q 来近似p时所造成的信息损失量。KL散度是按照概率分布q 的最优编码对真实分布为p的信息进行编码，其平均编码长度H(p, q)和p的最优平均编码长度H(p)之间的差异。对于离散概率分布p和q，从q 到p的KL散度定义为：

                                           

                                                           

其中为了保证连续性，定义：

                                              

KL散度可以是衡量两个概率分布之间的距离。KL散度总是非负的，DKL(p∥q) ≥0。只有当p = q 时，DKL(p∥q) = 0。如果两个分布越接近，KL散度越小；如果两个分布越远，KL散度就越大。但KL散度并不是一个真正的度量或距离，一是KL散度不满足距离的对称性，二是KL散度不满足距离的三角不等式性质。

3.3 JS 散度

JS散度是一种对称的衡量两个分布相似度的度量方式，定义为：

                                              

其中m =1/2(p + q)。

JS散度是KL散度一种改进。但两种散度有存在一个问题，即如果两个分布 p, q 个分布没有重叠或者重叠非常少时，KL 散度和 JS 散度都很难衡量两个分布的距离。

3.4 Wasserstein 距离

Wasserstein距离也是用于衡量两个分布之间的距离。对于两个分布q1, q2，pth-Wasserstein距离定义为：

                                           

其中Γ(q1, q2)是边际分布为q1 和q2 的所有可能的联合分布集合，d(x, y)为x和y 的距离，比如ℓp 距离等。

如果将两个分布看作是两个土堆，联合分布γ(x, y)看作是从土堆q1 的位置x到土堆q2 的位置y 的搬运土的数量，并有：

                                            

q1 和q2 为γ(x, y)的两个边际分布。

可以理解为在联合分布 γ(x, y) 下把形状为 q1 的土堆搬运到形状为q2 的土堆所需的工作量，

                                       

其中从土堆q1 中的点x到土堆q2 中的点y 的移动土的数量和距离分别为γ(x, y)和d(x, y)^p。因此，Wasserstein距离可以理解为搬运土堆的最小工作量，也称为推土机距离（。图E.1给出了两个离散变量分布的Wasserstein距离示例。图E.1c中同颜色方块表示在分布q1 中为相同位置。

Wasserstein距离相比KL散度和JS散度的优势在于：即使两个分布没有重叠或者重叠非常少，Wasserstein距离仍然能反映两个分布的远近。

对于 R^n 空间中的两个高斯分布 p = N (µ1, Σ1) 和 q = N (µ2, Σ2)，它们的2^nd-Wasserstein距离为:

          

当两个分布的的方差为0时，2^nd-Wasserstein距离等价与欧氏距离。