【3D计算机视觉】由单张2D图像生成3D点云的深度网络

《A Point Set Generation Network for 3D Object Reconstruction from a Single Image》论文笔记

1. 当时3D视觉的现状

3D视觉领域当我们尝试实现某些深度卷积结构时，我们常常面临着一个问题——现有的用于信号领域中的判别性和生成性学习的深度网络结构非常适合于规律的采样数据，例如图像，音频或视频；然而，最常见的一些3D几何表示，例如2D网格（mesh）或点云（point cloud）不是规则的结构，并且不适用于这些网络结构（当然后面出现了Pointnet）。这就是为什么大多数现存的工作都在使用深网进行3D 数据采用体积网格或图像集合（几何体的2D视图）。 然而，这种表示导致采样分辨率和净效率之间的折衷。 此外，它们还包含量化伪像（quantization artifacts），这些伪像会在刚性动作等情况下模糊数据的自然不变性。

2. 算法简介

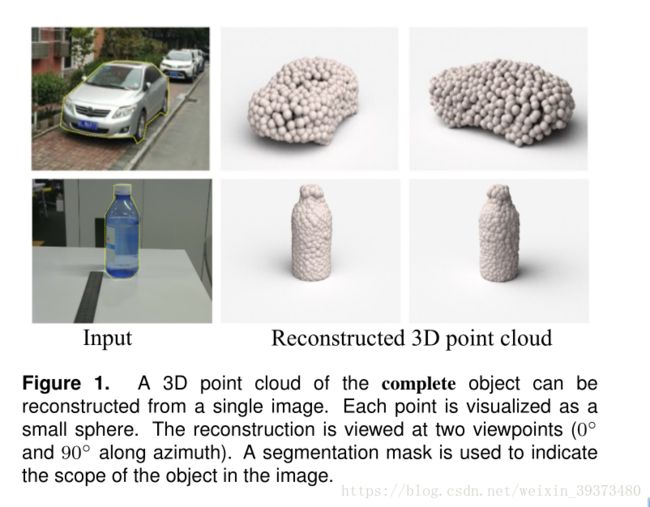
在这篇论文中，作者利用深度网络通过单张图像直接生成点云，解决了基于单个图片对象生成3D几何的问题。与使用几何图元（geometric primitives ）的CAD模型相比甚至简单的mesh相比，点云在表示基础连续3D几何图形时效率也许不高，但它也同时具有许多优点——点云是一种简单，统一的结构， 更容易学习，因为它不必编码多个基元或组合连接模式； 此外，点云可以在几何变换和变形时更容易操作，因为连接性不需要更新。 该网络可以由输入图像确定的视角推断的3D物体中实际包含点的位置。

鉴于这种非正统的网络输出，作者面临的挑战之一是如何在训练期间构造损失函数。因为相同的几何形状可能在相同的近似程度上可以用不同的点云来表示，因此与通常的L2型损失不同。本文使用两种距离函数作为解决方案。 本文利用其来保证速度并确保端end-to-end的训练。

本文试图通过使用某些先验知识来解决3D结构的单一投影图像恢复时的不确定性问题。网络的目标是估计图像的可见部分的深度，并对象几何体的非可见部分产生假想，并评估几种不同假想的可信度。 从统计学的角度来看，最理想的情况是我们能够完全复现出真实空间的景观，或者能够相应地对可信的候选人进行选择（允许一张图片有多重联想情况）。 如果我们将其视为回归问题，那么它在某些视角中必然存在固有的对象模糊性，从而存在多个同样好的3D重建方式，使得每个训练样本具有独特的注解，同样也使得训练独特于传统的分类/回归问题。 在这样的情境中，适当的损失函数的定义显得至关重要。

本文称最终算法是一个条件采样器（conditional sampler），它在给定输入图像的情况下，从‘’真像‘’空间中选择可信的点云。

该文章的贡献可归纳如下：

（1）开创了点云生成的先例（单图像3D重建）
（2）系统地探讨了体系结构中的问题点生成网络的损失函数设计
（3）提出了一种基于单图像任务的三维重建的原理及公式和解决方案

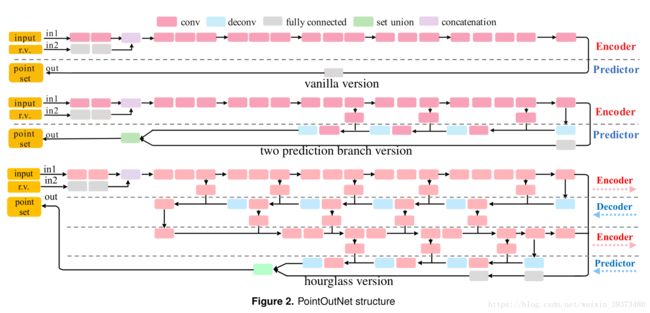
3. 网络结构及算法构想

模型最终的目标是给定一张单个的图片（RGB或RGB-D），重构出完整的3D形状，并将这个输出通过一种无序的表示——点云（Point cloud）来实现。点云中点的个数，文中设置为1024，作者认为这个个数已经足够表现大部分的几何形状。 点云的优势在于可以利用较少的、覆盖在物体表面的点来描述物体，并且当物体旋转或者重新调整尺度时，可以通过简单的线性变化得到新的图像（与体素不同）。

本文利用 Chamfer distance 和 Earth Mover’s distance构造损失函数，并在后面证明了这两个函数几乎在任何地方都可微。另外在模型构建的时候由于单个2D图像的局限性，即使是人也无法猜出正确的形状，因此从众多模棱两可的‘真像‘中预测结果也是一大难题。因此文中定义了预测出的真像集是一个概率分布$P(\bullet |I)$，其中I是输入图像，其训练的网络为 $G(I,r;\theta )$，其中$r$是一个正态分布的扰动项用来对I加入噪声$\theta$是网络的参数。

本文最终提出了三种网络结构，分别从简单到复杂。

• 最上面的（vanilla version）网络最简单，其直接通过一系列的conv层和RELU层，输出N x 3的点集$(x_i,y_i,z_i)$其中$i=1:N$。
• 第二个网络（two prediction branch version）进一步改进了预测网络的结构，由于第一个网络完全采用全连接的预测，因此不能较好的考虑3D物体的几何特征，第二个网络可以较好地适应大而光滑的物体表面特征。该网络有两个分支，全连接分支和反卷积分支。FC分支同第一个网络一样直接预测点集，反卷积分支直接预测大小为H×W的3通道图像，其中每个像素的三个值是一个点云上的点，其给出H×W个点，这些点后来合并在一起形成了整套点集M。该网络还添加多个跳跃连接以增强编码器和预测器的信息流通。反卷积结构的加入使得网络不仅有更多的权重共享，还更加适应光滑的物体表面的描述。
• 最下面的沙漏网络（hourglass version），可以反复进行解码和编码的过程，并能更好地混合局部与全局特征。

4. 损失函数

文中认为损失函数应该满足以下三点特征：
（1）全局可微
（2）计算便捷（因为要进行多次前向、反向传播）
（3）适用于稀疏点集
随后文中提出了如下损失函数的构想：

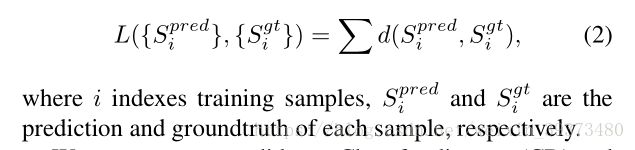
接下来，论文又给出了两个可以使用的距离函数用于构造损失函数：


5. 网络的实现
总体来说，由于2D转3D的不确定性，网络最终输出的是一个预测点的集合，作者希望网络会倾向于以平均的形式（Mean-shape）综合这些点输出一个最可信的形状。（下图可以看出两种Loss的情况下是如何平均可能的点集的）

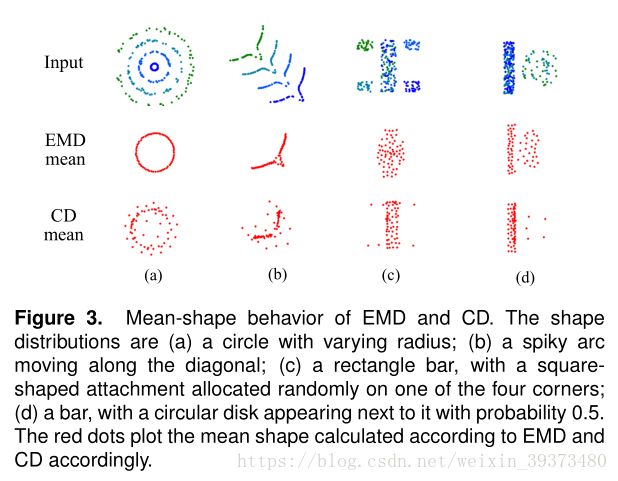
其次， 对于解决‘‘2D图片重构后可能的形状有很多种”这个问题，作者构造了如下两种解决方案：
1、其构造了一个 Min-of-N loss (MoN) 损失函数

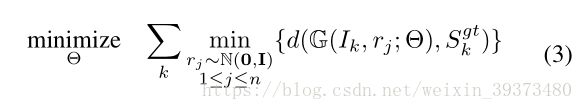
给定一个图像$I_k$，$S_k^{g}t$是数据的真实形状的点集，网络G通过n个不同的$r_j$扰动项进行n次预测（如下图），作者认为从直觉上来看，我们会相信n次中会至少有一次预测会非常接近真正的答案$S_k^{g}t$，因此可以认为这n次预测与真正的答案的距离d（Chamfer distance 和 Earth Mover’s distance）的最小值应该要最小。（在实验中作者发现这里n取到2就已经足够了）

2、另一种方法，作者用到了《Tutorial on variational autoencoders》中的 conditional variational autoencoder，具体可以去查看论文。

6. 实验结果
最后，作者的实验建立在 ShapeNet数据集上，里面包含了大量的人造3D物体模型，作者运用了其中220K个模型共2000类进行训练。

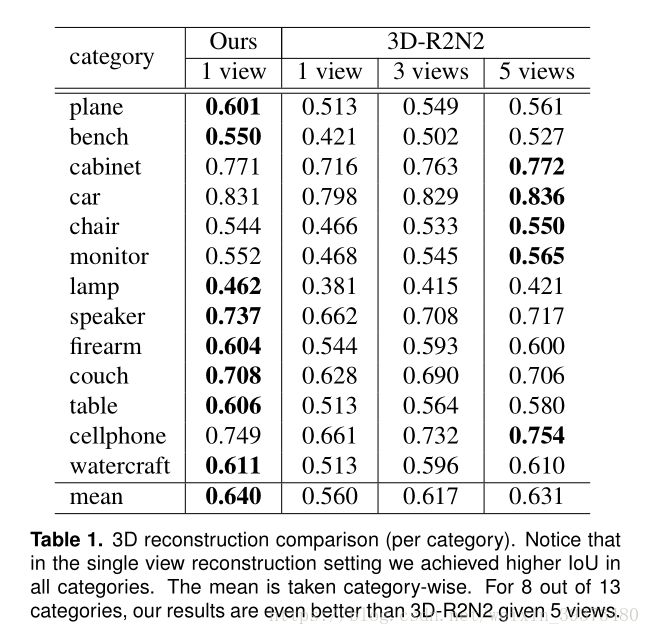
在最后的实验结果中，作者将自己的模型与3D-R2N2模型进行了对比，该模型是通过输入多尺度的图片对图像进行3D重构的深度模型。在13个物体类别中，作者模型预测结果的IOU在多项物体类别中的效果都超过了3D-R2N2多角度3D重构模型的预测效果：

此外，该算法可以应用于3D物体补全，效果较好：

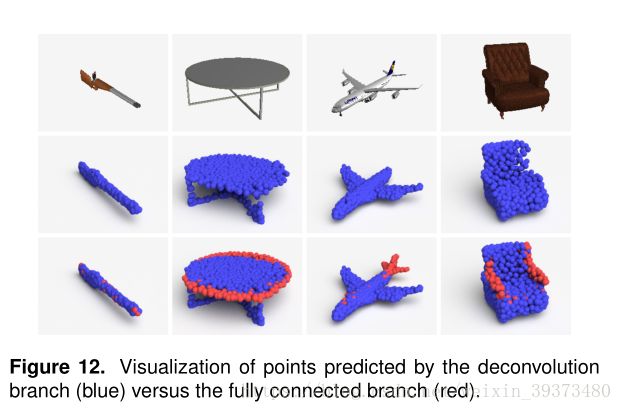
作者在实验中发现，反卷积结构在3D重建中更倾向于捕捉物体的主题部分（蓝色），而全连接结构更倾向于捕捉细节（红色）。

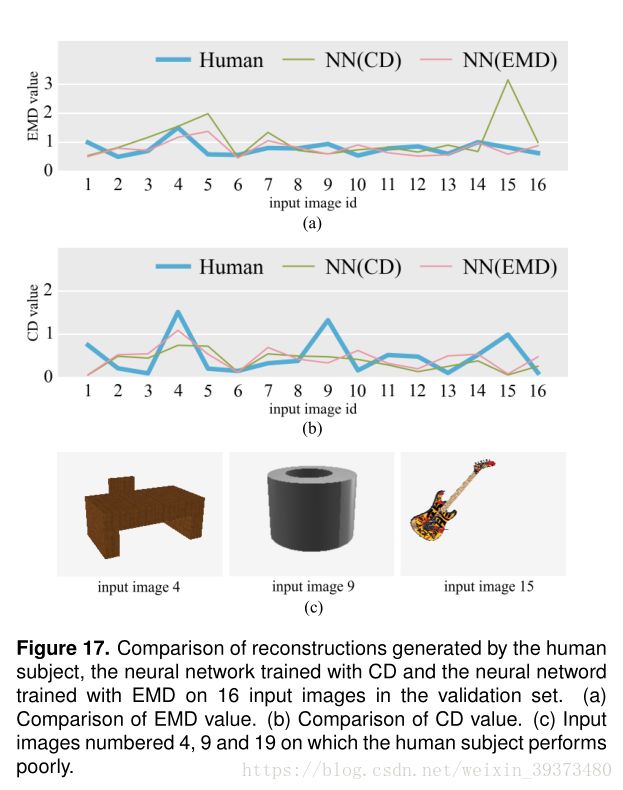
最后作者将该算法与人类的3D重构能力进行了对比，发现在某些物体上其胜过人来的想象力。

总体来说，该篇文章开创了单个2D视角重构3D物体的先河，是一篇值得一看的文章。