数据结构之图的应用（最小生成树之Kruskal算法实现）（C++）

最小代价生成树的3条构造准则：

1）.只能使用网络中的边来构造最小生成树；

2）.能且只能使用 n-1 条边来连接网络中的 n 个顶点；

3）.选用的 n-1 条边不能产生回路。

一、Kruskal算法简介

基本思想：对一n个顶点的连通网络 N={V, E}，其最小生成树是 T={V, TE}；

1.最小生成树T 中 V为网络N 中的全部顶点，TE 初始时为空；

2.初始时，T中每个顶点自成一个连通分量；

3.从网络的E中取最小代价边，若此边的两端顶点属于不同的连通分量，则将此边加入生成树的TE中；否则，舍去此边，选择下一条最小代价边。直到选出 n - 1 条最小代价边为止。

4.最小代价边用小根堆求解，判断顶点是否同属一个连通分量用并查集判断；

5.Kruskal算法时间复杂度为：O(log2(e))，即与边数有关，与顶点数无关，故适用于边稀疏的网的最小生成树的求解。

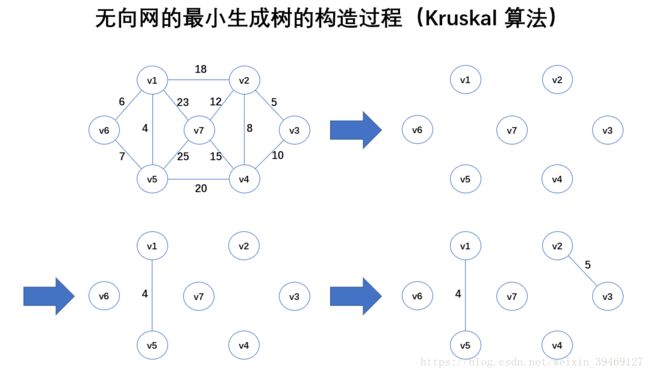
二、图解

三、代码

1.代码中包含的"GraphAdjMat.h"头文件，在之前博文“数据结构之图（邻接矩阵实现）”中；

2.代码中包含的"BiHeap.h"头文件，在之前博文“数据结构之二叉堆及堆排序”中；

3.代码中包含的"UFS.h"头文件，在之前博文“数据结构之并查集”中；

//文件名："MST_KRUSKAL.cpp"
#include "stdafx.h"
#include 
#include "GraphAdjMat.h"
#include "BiHeap.h"
#include "UFS.h"
using namespace std;

GraphAdjMat * GraphAdjMat::MiniSpanTree_Kruskal()
{
	/*
	.	最小（代价）生成树：( Minimum  Cost Spanning Tree )
	.		入参：
	.			string * vertex: 起始顶点
	.		出参：
	.			GraphAdjList *: 生成树的图对象
	.		算法实现：（ Kruskal 算法 ）
        .		时间复杂度：O(log2(e))
	.
	*/
	//判断是否为无向网
	if (this->type != UDN)
		return NULL;

	//1.将连通图所有边加入到二叉堆中，并构建成小根堆
	//1.1.初始化二叉堆参数：a).小根堆；b).图的边总数；c).堆元素关键字Key比较接口实现
	BiHeap * heap = new BiHeap(
		BiHeap::MIN, this->arcNum, 
		[](int * arc1, int * arc2) {
		//用 int[3]{ i, j, weight } 数组表示边，关键字Key 为 arc[2]
		if (arc1[2] > arc2[2])
			return 1;
		else if (arc1[2] > arc2[2])
			return -1;
		else
			return 0;
	});
	//1.2.遍历图所有边，将边数据插入小根堆
	for (int i = 0; i < this->vexNum; i++)
	{
		for (int j = 0; j < this->vexNum; j++)
		{
			//只将权重为非无穷的边插入堆
			if (this->arcs[i][j].adj == this->_INFINITY)
				continue;
			//用 int[3]{i, j, weight} 数组表示边
			heap->Insert(new int[3]{i, j, this->arcs[i][j].adj });
		}
	}
	//1.3.构建小根堆
	heap->Build();
	//2.创建顶点并查集：初始化顶点总数
	UFS * ufs = new UFS(this->vexNum);

	
	//初始化最小生成树 图
	GraphAdjMat * mst = new GraphAdjMat(GraphAdjMat::UDN);
	mst->Init(new ObjArrayList(), new ObjArrayList());
	//3.根据MST性质，寻找 n-1 条（顶点数 - 1）最小代价边
	int * arc = NULL;
	int count = 1;
	while (count < this->vexNum)
	{
		//3.1.从小根堆中取出最小代价边
		arc = heap->GetRoot();
		//3.2.合并边顶点：
		//3.2.1.若两顶点所属集合连通，不合并，寻找下一条边
		//3.2.2.若两顶点所属集合不连通，合并
		if (ufs->Union(arc[0], arc[1]))
		{
			//向生成树图中插入边，顶点
			mst->InsertVertex(new string(this->vexs[arc[0]]));
			mst->InsertVertex(new string(this->vexs[arc[1]]));
			mst->InsertArc(new ArcData{ this->vexs[arc[0]], this->vexs[arc[1]], arc[2]});
			//最小代价边计数
			count++;
		}
	}
	//4.返回最小生成树
	return mst;
}

//文件名："MST_KRUSKAL_Test.cpp"
#include "stdafx.h"
#include 
#include "GraphAdjMat.h"
#include "ObjArrayList.h"
using namespace std;

int main()
{
	//初始化顶点数据
	string * v1 = new string("v1");
	string * v2 = new string("v2");
	string * v3 = new string("v3");
	string * v4 = new string("v4");
	string * v5 = new string("v5");
	string * v6 = new string("v6");
	string * v7 = new string("v7");
	ObjArrayList * vexs = new ObjArrayList();
	vexs->Add(v1);
	vexs->Add(v2);
	vexs->Add(v3);
	vexs->Add(v4);
	vexs->Add(v5);
	vexs->Add(v6);
	vexs->Add(v7);

	//初始化边（弧）数据
	GraphAdjMat::ArcData * arc0 = new GraphAdjMat::ArcData{ "v1", "v2", 18 };
	GraphAdjMat::ArcData * arc1 = new GraphAdjMat::ArcData{ "v1", "v7", 23 };
	GraphAdjMat::ArcData * arc2 = new GraphAdjMat::ArcData{ "v1", "v6", 6 };
	GraphAdjMat::ArcData * arc3 = new GraphAdjMat::ArcData{ "v1", "v5", 4 };
	GraphAdjMat::ArcData * arc4 = new GraphAdjMat::ArcData{ "v2", "v7", 12 };
	GraphAdjMat::ArcData * arc5 = new GraphAdjMat::ArcData{ "v2", "v3", 5 };
	GraphAdjMat::ArcData * arc6 = new GraphAdjMat::ArcData{ "v2", "v4", 8 };
	GraphAdjMat::ArcData * arc7 = new GraphAdjMat::ArcData{ "v3", "v4", 10 };
	GraphAdjMat::ArcData * arc8 = new GraphAdjMat::ArcData{ "v4", "v7", 15 };
	GraphAdjMat::ArcData * arc9 = new GraphAdjMat::ArcData{ "v4", "v5", 20 };
	GraphAdjMat::ArcData * arc10 = new GraphAdjMat::ArcData{ "v5", "v7", 25 };
	GraphAdjMat::ArcData * arc11 = new GraphAdjMat::ArcData{ "v5", "v6", 7 };
	ObjArrayList * arcsList = new ObjArrayList();
	arcsList->Add(arc0);
	arcsList->Add(arc1);
	arcsList->Add(arc2);
	arcsList->Add(arc3);
	arcsList->Add(arc4);
	arcsList->Add(arc5);
	arcsList->Add(arc6);
	arcsList->Add(arc7);
	arcsList->Add(arc8);
	arcsList->Add(arc9);
	arcsList->Add(arc10);
	arcsList->Add(arc11);

	//测试：无向网最小生成树 Kruskal 算法
	cout << endl << "无向网初始化：";
	GraphAdjMat * udn = new GraphAdjMat(GraphAdjMat::UDN);
	udn->Init(vexs, arcsList);
	udn->Display();
	GraphAdjMat * mst = udn->MiniSpanTree_Kruskal();
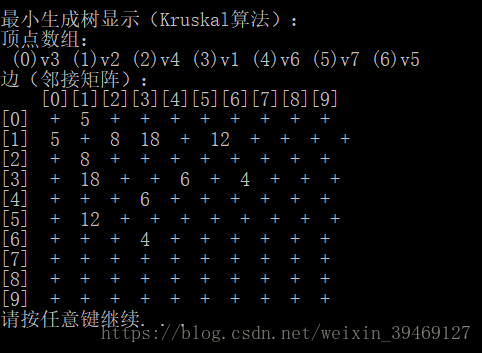
	cout << endl << "最小生成树显示（Kruskal算法）：";
	mst->Display();
	
	return 0;
}

四、输出结果