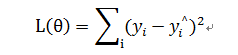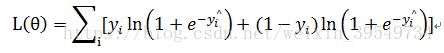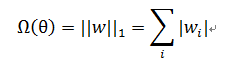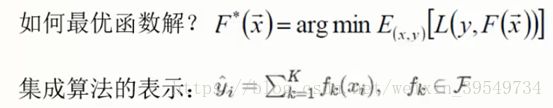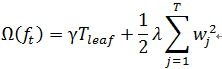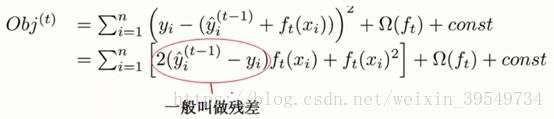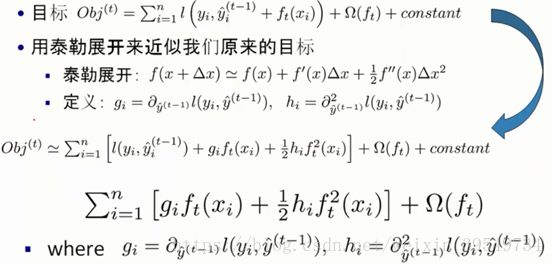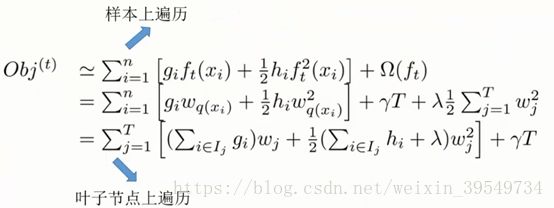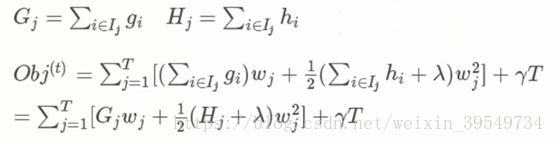Xgboost算法

一、Boosting方法

1.  XGBoost（Extreme Gradient Boosting）

    XGBoost是一种梯度提升算法、残差决策树，其基本思想为：一棵树一棵树逐渐地往模型里面加，每加一棵CRAT决策树时，要使得整体的效果（目标函数有所下降）有所提升。使用多棵决策树（多个单一的弱分类器）构成组合分类器，并且给每个叶子节点赋与一定的权值。

    这里所讲的决策树是分类与回归树CRAT（classification and regression tree,CART）。CART决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。CART会把输入根据属性分配到各个叶子节点上，而每个叶子节点上面会对应一个分数值（权值）。

2.  GBDT

    传统GBDT以CART作为基分类器，在优化时只用到一阶导数信息，

    Boosting Tree树数据挖掘和机器学习中常用算法之一，其对输入要求不敏感，效果好，在工业界用的较多。

 

二、训练误差（Train loss）与正则化惩罚项（Regularization）

    目标函数=训练误差+正则化惩罚项

1. 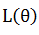：训练误差或损失函数，度量模型预测值与真实值的误差

   常见损失函数有

--均方误差损失函数

--logistic损失函数

2. 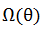：正则化惩罚项，度量模型的复杂度，避免过拟合

    常用的正则化惩罚项有

A．L1 正则化（1-范数）：对模型参数 的L1正则项

    设带L1正则化的损失函数：

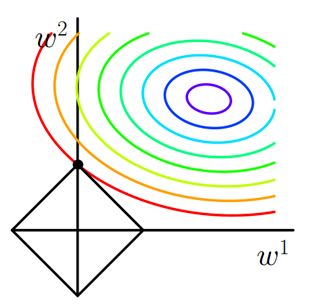
    假设损失函数在二维上求解，则可以画出图像

    彩色实线是J0的等值线，黑色实线是L1正则的等值线。二维空间（假设权重向量只有w1和w2）上，L1正则项的等值线是方形，方形与J0的等值线相交时，相交点为顶点的概率很大，w1或w2等于零的概率很大。所以使用L1正则项的解具有稀疏性。

    用途：由L1正则化导出的稀疏性质已被广泛用于特征选择，特征选择可以从可用的特征子集中选择有意义的特征。

 

B．L2正则化（2-范数）：对模型参数 的L2正则项

    即权重向量 中各个元素的平方和； a：通常取1/2。L2正则也经常被称作“权重衰减”（weight decay）和“岭回归”

    设带L2正则化的损失函数：

    假设损失函数在二维上求解，则可以画出图像

 

    彩色实线是J0的等值线，黑色实线是L2正则的等值线。二维空间（假设权重向量只有w1和w2）上，L2正则项的等值线是圆，圆与J0的等值线相交时，w1或w2等于零的概率很小。所以使用L2正则项的解不具有稀疏性。

    用途：L2通常倾向让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。参数足够小，数据偏移得多一点也不会对结果造成什么影响，可以说“抗扰动能力强”。

    L1和L2正则是比较常见和常用的正则化项，都可以达到防止过拟合的效果。

    下面补充范数的概念

1-范数：║x║1=│x1│+│x2│+…+│xn│

--即向量元素绝对值之和

2-范数：║x║2=（│x1│2+│x2│2+…+│xn│2）1/2

--Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方

∞-范数：║x║∞=max（│x1│，│x2│，…，│xn│），即所有向量元素绝对值中的最大值

-∞-范数：║x║-∞=min（│x1│，│x2│，…，│xn│），即所有向量元素绝对值中的最小值

p-范数：║x║p=（│x1│p+│x2│p+…+│xn│p）1/p，即向量元素绝对值的p次方和的1/p次幂

 

三、推导目标函数

案例

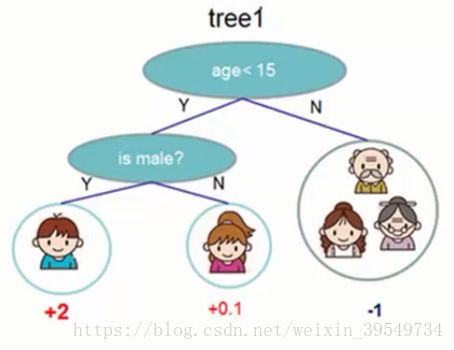
    下面的例子是预测一个人喜欢电脑游戏可能性（回归问题）。将叶子节点的权值表示为分数后，可以做概率预测，排序等等。

 

    一个CART往往过于简单，而无法有效的进行预测，因此更加高效的是使用多个CART进行融合，使用集成的方法提升预测效率。

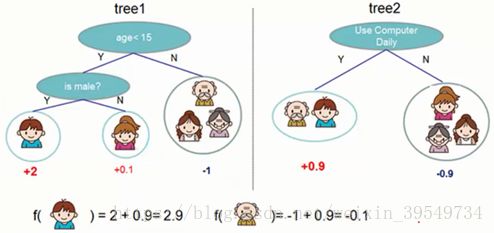
    假设有两颗回归树，则两棵树融合后的预测结果如下图所示。

 

 

1.训练误差（损失函数）

预测值：

   --样本xij与权值wj的线性组合

   -- wj：叶子节点的权值

   --第i个样本在一棵决策树上第j个叶子节点的加权累加和

训练误差（损失函数）：
   --损失函数（越小越好）不唯一，这里采用均方误差的方法计算

   --第i样本在一棵决策树上的均方误差

最优函数解：

   --所有样本在一棵决策树上的训练误差的数学期望（平均值）的最小值

   -- argmin f(x)：指使得函数f(x)取得其最小值的所有自变量x的集合。比如，函数cos(x)在±π、±3π、±5π、…处取得最小值（-1），则argmin cos(x) = {±π,±3π,±5π,...}。如果函数 f(x)只在一处取得其最小值，则 argmin f(x)为单点集，比如 argmin (x-4)^2 =4。

 

2.正则化惩罚项

    当目前为止，讨论了模型中训练误差的部分。下面来探讨模型复杂度 的表示方式。

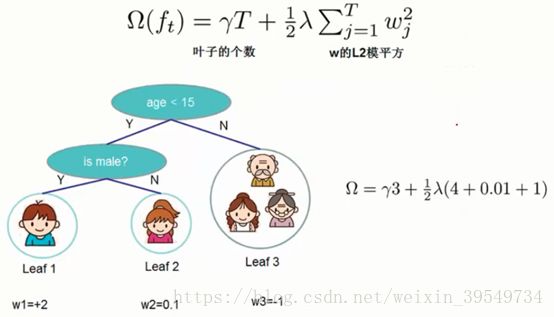
    类似于决策树与随机森林，为了防止过拟合的风险过高，要限制叶子节点的个数，因此引入正则化惩罚项（损失函数） ：

   -- 越小越好

   -- γ：惩罚系数（人工设置），该值越大，说明叶子节点数的惩罚力度越大，损失值也就越大；反之亦然

   -- Tleaf：叶子节点数，该值越大损失越大

   -- ：对于w权值参数的正则化惩罚项（L2正则化），类似于线性回归，神经网络， a取1/2

 

3.目标函数

    综上所述，目标函数由两部分组成：训练误差（均方误差）+损失函数 （正则化惩罚项）。目标函数不仅要优化预测值与真实值之间的差异，还要考虑过拟合的风险。

 

四、优化目标函数

  

    现在还剩下一个问题 ，如何选取每一轮加入什么呢？答案是非常简单的，选取一个f来使得目标函数尽可能最大的降低

    在每一轮加入一棵树时，都要把前面的树当成一个整体，然后计算出一个残差值，加进来的树通过优化残差值来使得残差值最小

    目标函数的化简推导

   不考虑常数项，常数项对优化求解是没有影响的

i：样本

n：样本总数

j：叶子节点

T：叶子节点总数

k：决策树

K：决策树总数

    将对样本的遍历转换为对叶子节点的遍历（然后在叶子节点里面再对样本进行遍历），遍历样本和遍历叶子节点实际上是一样的，因为最后所有的样本都会落到叶子节点上。

    每一个叶子节点都要计算里面所有样本的一阶导、二阶导的累加和（因为每一个样本的一阶导、二阶导都不一样）

    用推导出来的目标函数来决定决策树的构造过程（在哪里切割），分别计算在不同地方切割的增益值，然后进行比较即可

 

五、利用目标函数构造决策树

    Obj代表了当我们指定一个树的结构的时候，我们在目标上面最多减少多少，我们可以把它叫做结构分数。类似于Gini系数一样更加一般的对于树结构进行打分的函数。

    下面是一个具体的打分函数计算的例子。

更多AI资源请关注公众号：大胡子的AI

欢迎各位AI爱好者加入群聊交流学习：882345565（内有大量免费资源哦！）

版权声明：本文为博主原创文章，未经博主允许不得转载。如要转载请与本人联系。