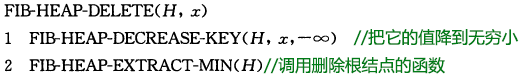《算法导论》第十九章——斐波那契堆

  虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！

可合并堆

可合并堆是支持以下5种操作的一种数据结构，其中每个元素都有一个关键字：

MakeHeap()：创建和返回一个新的不含任何元素的堆
Insert(H,x)：将一个已填入关键字的元素x插入堆H中
Minimum(H)：返回一个指向堆H中具有最小关键字的元素的指针
ExtractMin(H)：从堆H中删除具有最小关键字的元素，并返回一个指向该元素的指针
Union(H1,H2)：创建并返回一个包含堆H1和堆H2中所有元素的堆。堆H1与堆H2则销毁。

斐波那契堆还支持：

DecreaseKey(H,x,k)：将堆H中的元素x的关键字赋予新值k。k不大于当前关键字。
Delete(H,x)：从堆H中删除元素x

19.1斐波那契堆结构

一个斐波那契堆是一系列具有最小堆序的有根树的集合。

每个结点包含

x.p指向父结点的指针
x.child指向它某个孩子的指针
x.degree储存孩子数目
x.mark指示上一次成为另一个结点的孩子后，是否失去过孩子
每个孩子y都有指针y.left和y.right，分别指向左右兄弟

x的所有孩子被链接成一个环形的双向链表，成为x的孩子链表。（各兄弟出现顺序任意）
孩子链表的优点：
1、可以在O(1)时间内从一个环形链表的任何位置插入一个结点或删除一个结点
2、给定两个链表，可以用O(1)时间把它们连接

所有树的根都用left与right连接在一起，成为根链表

势函数

t(H)：H根链表中树的数目
m(H)：H中已经标记的结点
则势函数：θ(H)=t(H)+2m(H)

19.2可合并操作堆

①创建一个新的斐波那契堆

H.min：斐波那契堆中最小的结点
H.n：斐波那契堆的结点数量

H.min初始化为NULL
H.n初始化为0

②插入一个结点

③寻找最小结点(没有写函数)
其实就是H.min

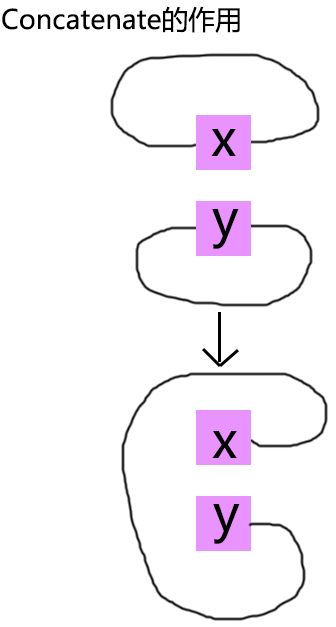
④两个斐波那契堆的合并
简单地合并H1与H2，并且把H.min更新为两个中小的那个。

第3行函数Concatenate：

⑤抽取最小结点

这边写的有点复杂，我就精简一下：
步骤一：去掉根结点，把它的所有孩子都放入根链表
步骤二：努力地把根链表中散落的数串在一起，使得斐波那契堆里所有的树都不一样高！
步骤二的实现可能比较麻烦，具体的图解我们可以参考一下skywang12345的博客，我觉得他的图画的就十分不错，也是在抽取最小结点那个地方。
附上链接：
https://www.cnblogs.com/skywang12345/p/3659069.html

Consolidate的作用原理：

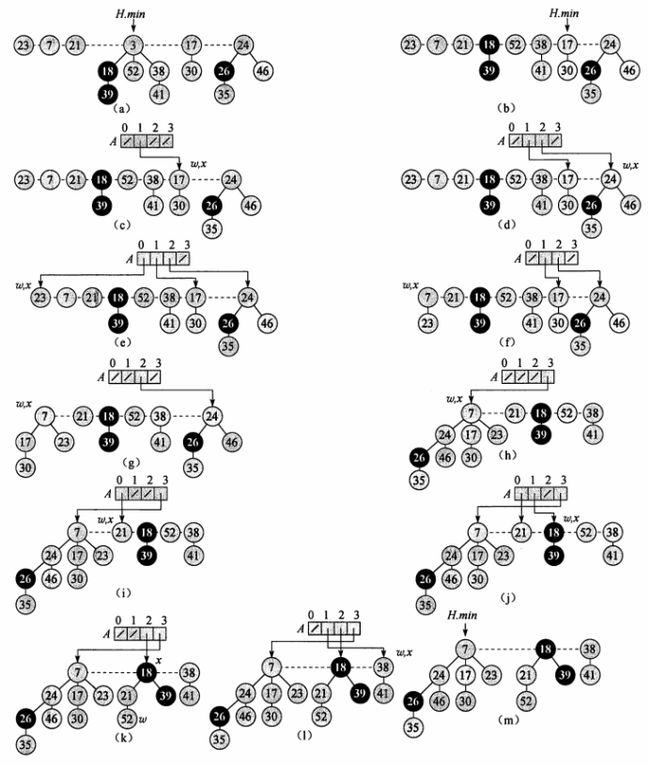
这边我对Consolidate想了很久，终于想通了它的原理：A的一个指向根结点的数组。A[0]存的是degree=0的根，A[1]存的是degree=1的根…我们来看一下书中的例图：这边我们看到（c）中A[1]保存了一棵高度为1的树，接下来在（d）中A[2]保存了一棵高度为2的数，（e）中A[0]保存了一棵高度为0的数，但是到了（f）图的时候，根⑦的高度也是0，我们看到在伪代码第7行中while(A[d]≠NIL)，这里就要进入循环了，于是我们把⑦与23合并在一起，变成了一棵高度为1的树。然后把高度为0的地方A[0]重新置为NULL。（伪代码第12行）这个时候又起冲突了！这棵树与我们原来保存的高度为1，根为17的树撞在了一起，于是我们又要合并这两棵树，变成了一棵高度为3的数。然后继续判断。

19.3关键字减值和删除一个结点

⑥关键字减值

⑦删除一个结点

好了接下来就是代码部分了。建议粘贴到自己的编辑中运行（我不知道为什么我的代码就是没有彩色的，感觉影响观看，可能 我比较菜吧！）：

斐波那契堆.h

#pragma once
#define D 5

/*斐波那契堆结点*/
typedef struct FibNode
{
	int key;			/*关键字值*/
	int degree;			/*最大度数*/
	FibNode* left;		/*左兄弟*/
	FibNode* right;		/*右兄弟*/
	FibNode* parent;	/*父结点*/
	FibNode* child;		/*孩子结点*/
	bool mark;			/*是否被删除第一个孩子*/
}FibNode;
/*斐波那契堆*/
typedef struct FibHeap
{
	FibNode* min;
	int n;/*结点个数*/
}FibHeap;

/*产生一个新的结点*/
FibNode* CreateFibNode(int data);
/*①新建一个斐波那契堆*/
FibHeap* MakeFibHeap();

/*插入函数，y是新节点*/
void InsertHeap(FibNode* x, FibNode* y);
/*②插入一个新的结点*/
void FibInsert(FibHeap* &H, FibNode* x);

/*合并函数*/
void Concatenate(FibNode* x, FibNode* y);
/*④两个斐波那契堆的合并*/
FibHeap* FibHeapUnion(FibHeap* &H1, FibHeap* &H2);

/*抽取最小节点的辅助函数*/
void NodeRemove(FibNode* x);
/*抽取最小节点的辅助函数*/
void FibHeapLink(FibHeap* &H, FibNode* x, FibNode* y);/*y成为x的孩子*/
/*抽取最小节点的辅助函数*/
void Consolidate(FibHeap* &H);
/*⑤抽取最小结点*/
FibNode* FibHeapExtractMin(FibHeap* &H);

/*切断*/
void NodeCut(FibHeap* &H, FibNode* x, FibNode* y);
/*级联切断*/
void CascadingCut(FibHeap* &H, FibNode* y);
/*⑥关键字减值*/
void FibHeapDecreaseKey(FibHeap* &H, FibNode* x, int k);

/*⑦删除一个结点*/
void FibHeapDelete(FibHeap* &H, FibNode* x);

/*打印辅助*/
void Print_1(FibNode* x, FibNode* prev, int direction);
/*打印斐波那契堆*/
void FibPrint(FibHeap* &H);

/*测试程序*/
void TestFibHeap();

斐波那契堆.cpp

#include "斐波那契堆.h"
#include
#include
#include
using namespace std;

/*产生一个新的结点*/
FibNode* CreateFibNode(int data)
{
	FibNode* fn = new FibNode();
	if (fn != NULL)
	{
		fn->parent = NULL;
		fn->child = NULL;
		fn->left = NULL;
		fn->right = NULL;
		fn->key = data;
		fn->mark = false;
	}
	else
	{
		cout << "开辟结点失败！" << endl;
	}
	return fn;
}
/*①新建一个斐波那契堆*/
FibHeap* MakeFibHeap()
{
	FibHeap* H = new FibHeap();
	if (H == NULL)
		cout << "创建失败！" << endl;
	H->min = NULL;
	H->n = 0;
	return H;
}
/*插入函数，y是新节点*/
void InsertHeap(FibNode* x, FibNode* y)
{
	y->left = x->left;
	y->right = x;
	y->right->left = y;
	y->left->right = y;
}
/*②插入一个新的结点*/
void FibInsert(FibHeap* &H, FibNode* x)
{
	if (!H->min)/*如果斐波那契堆是空的*/
	{
		x->left = x;
		x->right = x;
		H->min = x;
	}
	else
	{
		InsertHeap(H->min, x);
		if (x->key < H->min->key)/*有必要的话，更新H.min*/
			H->min = x;
	}
	H->n++;/*结点数量+1*/
}
/*合并函数*/
void Concatenate(FibNode* x, FibNode* y)
{
	FibNode* tmpx = x->left;
	FibNode* tmpy = y->left;
	x->left = y;
	tmpy->right = x;
	y->left = x;
	tmpx->right = y;
}
/*④两个斐波那契堆的合并*/
FibHeap* FibHeapUnion(FibHeap* &H1, FibHeap* &H2)
{
	if (!H1)return H2;/*如果H1为空，就直接返回H2*/
	if (!H2)return H1;/*如果H2为空，就直接返回H1*/

	Concatenate(H1->min, H2->min);

	if (H2->min->key < H1->min->key)
		H1->min = H2->min;
	H1->n += H2->n;
	return H1;
}
/*抽取最小节点的辅助函数*/
void NodeRemove(FibNode* x)
{
	x->left->right = x->right;
	x->right->left = x->left;
}
/*抽取最小节点的辅助函数*/
void FibHeapLink(FibHeap* &H, FibNode* x, FibNode* y)/*y成为x的孩子*/
{
	NodeRemove(y);/*把y从根链表中移除*/
	if (!x->child)/*如果x没有孩子*/
	{
		x->child = y;
		y->left = y;
		y->right = y;
	}
	else
	{
		InsertHeap(x->child, y);
	}
	y->parent = x;
	x->degree++;
	y->mark = false;
}
/*抽取最小节点的辅助函数*/
void Consolidate(FibHeap* &H)
{
	FibNode* A[D + 1] = { NULL };
	FibNode* sentinel = H->min->left;/*哨兵*/
	bool flag = true;
	
	for (FibNode* w = H->min, *next; flag; w = next)/*处理每个根结点*/
	{
		if (w == sentinel)/*只有一个结点*/
			flag = false;
		next = w->right;
		FibNode* x = w;
		int d = x->degree;

		while (A[d])
		{
			FibNode* y = A[d];
			if (x->key > y->key)/*查找最小节点*/
			{
				FibNode* tmp = x;
				x = y;
				y = tmp;
			}
			FibHeapLink(H, x, y);
			A[d++] = NULL;
		}
		A[d] = x;
	}
	H->min = NULL;
	for (int i = 0; i <= D; i++)
	{
		if (A[i])
		{
			if (!H->min)/*根结点为空*/
			{
				A[i]->left = A[i]->right = A[i];
				H->min = A[i];
			}
			else
			{
				InsertHeap(H->min, A[i]);
				if (A[i]->key < H->min->key)
					H->min = A[i];
			}
		}
	}
}
/*⑤抽取最小结点*/
FibNode* FibHeapExtractMin(FibHeap* &H)
{
	FibNode* z = H->min;
	if (z)
	{
		bool flag = true;
		for (FibNode* x = z->child, *next; x&&flag; x = next)
		{
			next = x->right;
			if (next == z->right)/*只有根结点*/
				flag = false;
			InsertHeap(H->min, x);
			x->parent = NULL;
		}
		NodeRemove(z);
		if (z == z->right)
			H->min = NULL;
		else
		{
			H->min = z->right;
			Consolidate(H);
		}
		H->n--;
	}
	return z;
}
/*切断*/
void NodeCut(FibHeap* &H, FibNode* x, FibNode* y)
{
	if (x == x->right)/*只有x一个孩子*/
		y->child = NULL;
	else
	{
		if (x == y->child)
			y->child = x->left;
		NodeRemove(x);
	}
	y->degree--;
	InsertHeap(H->min, x);/*把x插入根链表*/
	x->parent = NULL;
	x->mark = false;

}
/*级联切断*/
void CascadingCut(FibHeap* &H, FibNode* y)
{
	FibNode* z = y->parent;
	if (z)
	{
		if (!y->mark)
			y->mark = true;
		else
		{
			NodeCut(H, y, z);
			CascadingCut(H, y);
		}
	}
}
/*⑥关键字减值*/
void FibHeapDecreaseKey(FibHeap* &H, FibNode* x, int k)
{
	if (k > x->key)
	{
		cout << "数值错误";
		return;
	}
	x->key = k;
	FibNode* y = x->parent;
	if (y&&x->key < y->key)
	{
		NodeCut(H, x, y);
		CascadingCut(H, y);
	}
	if (x->key < H->min->key)
		H->min = x;
}
/*⑦删除一个结点*/
void FibHeapDelete(FibHeap* &H, FibNode* x)
{
	FibHeapDecreaseKey(H, x, -100);
	FibHeapExtractMin(H);
}
/*打印辅助*/
void Print_1(FibNode* x, FibNode* prev, int direction)
{
	FibNode* start = x;
	if (x == NULL)return;
	do
	{
		if (direction == 1)
		{
			cout <<"  "<< x->key << "(" << x->degree << ")是" << prev->key << "的孩子" << endl;
		}
		else
		{
			cout <<"  "<< x->key << "(" << x->degree << ")是" << prev->key << "的后一个数" << endl;
		}
		if (x->child != NULL)
			Print_1(x->child, x, 1);
		prev = x;
		x = x->right;
		direction = 2;	
	} while (x != start);
}
/*打印斐波那契堆*/
void FibPrint(FibHeap* &H)
{
	int i = 0;
	FibNode* p;
	if (H->min == NULL)
		return;
	cout << "斐波那契堆：" << endl;
	p = H->min;
	do
	{
		i++;
		cout << i << "." << p->key << "(" << p->degree << ")是根" << endl;
		Print_1(p->child, p, 1);
		p = p->right;
	} while (p != H->min);
	cout << endl;
	cout << endl;
}

/*测试程序*/
void TestFibHeap()
{
	FibHeap* H= MakeFibHeap();
	FibNode* y = CreateFibNode(0);
	FibNode* z = CreateFibNode(0);
	for (int i = 0; i < 10; i++)
	{
		FibNode* x = CreateFibNode((i+1)*10);
		if (i == 5)
			y = x;
		if (i == 6)
			z = x;
		FibInsert(H, x);
	}
	cout << "①我们初始的斐波那契堆：" << endl;
	FibPrint(H);

	cout << "②抽取最小值后：" << endl;
	FibHeapExtractMin(H);
	FibPrint(H);

	cout << "③我们把60降到5" << endl;
	FibHeapDecreaseKey(H, y, 5);
	FibPrint(H);

	cout << "④删除70后" << endl;
	FibHeapDelete(H, z);
	FibPrint(H);

	cout << "建立一个只有结点8的堆，合并两个堆" << endl;
	FibHeap* H2 = MakeFibHeap();
	FibNode* w = CreateFibNode(8);
	FibInsert(H2, w);
	H2 = FibHeapUnion(H, H2);
	FibPrint(H2);
}

主函数

#include "斐波那契堆.h"
#include 

int main()
{
	TestFibHeap();
	getchar();
	getchar();
	return 0;
}

运行结果