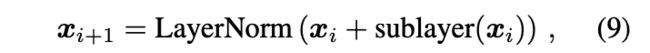ReZero is All You Need: Fast Convergence at Large Depth
ReZero is All You Need: Fast Convergence at Large Depth
Abstract
Deep networks have enabled significant performance gains across domains, but they often suffer from vanishing/exploding gradients. This is especially true for Transformer architectures where depth beyond 12 layers is difficult to train without large datasets and computational budgets. In general, we find that inefficient signal propagation impedes learning in deep networks. In Transformers, multi-head self-attention is the main cause of this poor signal propagation. To facilitate deep signal propagation, we propose ReZero, a simple change to the architecture that initializes an arbitrary layer as the identity map, using a single additional learned parameter per layer. We apply this technique to language modeling and find that we can easily train ReZero-Transformer networks over a hundred layers. When applied to 12 layer Transformers, ReZero converges 56% faster on enwiki8. ReZero applies beyond Transformers to other residual networks, enabling 1,500% faster convergence for deep fully connected networks and 32% faster convergence for a ResNet-56 trained on CIFAR 10.
深度网络已实现跨域的显着性能提升,但它们经常遭受梯度消失/爆炸的困扰。对于Transformer架构尤其如此,如果没有大型数据集和计算预算,则很难训练超过12层的深度。总的来说,我们发现无效的信号传播会阻碍深度网络中的学习。在transformer中,多头自我关注是这种不良信号传播的主要原因。为了促进深度信号传播,我们提出了ReZero,这是对体系结构的简单更改,该体系结构将任意层初始化为身份映射,并在每层使用单个额外的学习参数。我们将此技术应用于语言建模,发现可以轻松地在一百层上训练ReZero-Transformer网络。当应用于12层变压器时,ReZero在enwiki8上的收敛速度提高了56%。 ReZero不仅将Transformers应用于其他残余网络,还为深度完全连接的网络提供了1,500%的融合,而在CIFAR 10上接受培训的ResNet-56的融合则提高了32%。
1 Introduction
Deep learning has enabled significant improvements in state-of-the-art performance across domains [1, 2, 3, 4]. The expressivity of neural networks typically grows exponentially with depth [5], enabling strong generalization performance, but often induces vanishing/exploding gra- dients and poor signal propagation through the model [6]. Researchers have relied on careful initialization [7, 8] and normalization techniques such as BatchNorm [9] and LayerNorm [10] to mitigate this issue, but these techniques can be costly and limited.
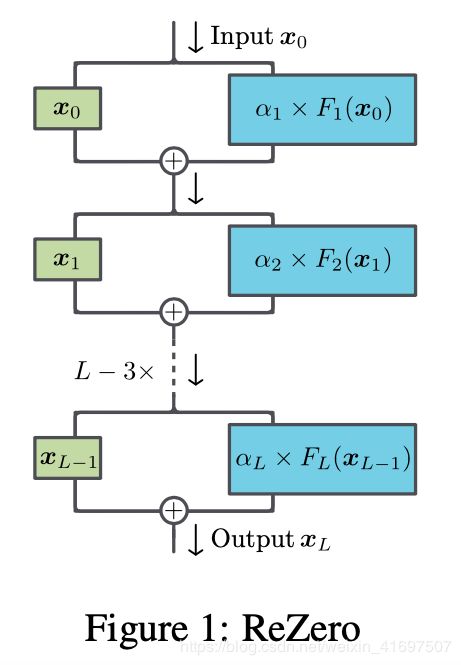
In this work, we propose ReZero2, a small architectural addition that dynamically facilitates well-behaved gradients and arbitrarily deep signal propagation. The idea is simple: ReZero initializes each layer to perform the identity operation. For each layer, we introduce a residual connection for the input signal x and one trainable parameter α that modulates the non-trivial transformation of the layer F (x),
xi+1 =xi +αiF(xi), (1)
深度学习已实现跨域的最新性能的显着改善[1、2、3、4]。 神经网络的表现力通常随深度呈指数增长[5],从而实现强大的泛化性能,但通常会导致消失/爆炸的梯度以及通过模型传播的不良信号[6]。 研究人员依靠仔细的初始化[7,8]和标准化技术(例如BatchNorm [9]和LayerNorm [10])来缓解此问题,但是这些技术可能会昂贵且受限制。
在这项工作中,我们提出了ReZero2,这是一种小的体系结构添加,可动态促进行为良好的渐变和任意深度的信号传播。 这个想法很简单:ReZero初始化每个层以执行标识操作。 对于每一层,我们为输入信号x和一个可训练参数α引入残差连接,该可调制参数α调制层F(x)的非平凡变换,
xi + 1 = xi +αiF(xi),(1)
![]()
where α = 0 at the beginning of training. Initially the gradients for all parameters defining F vanish, but dynamically evolve to suitable values during initial stages of training. We illustrate the architecture in Figure 1.
在训练开始时α= 0。 最初,所有定义F的参数的梯度都会消失,但会在训练的初始阶段动态演变为合适的值。 我们在图1中说明了该体系结构。
Code for ReZero applied to various neural architectures: https://github.com/majumderb/rezero
Table 1: Various forms of normalization and residual connections. F represents the transformation of an arbitrary layer and “Norm” is a normalization (e.g., LayerNorm or BatchNorm).
表1:各种形式的规范化和残留连接。 F表示任意层的变换,“范数”是归一化(例如LayerNorm或BatchNorm)。

ReZero provides two main benefits:
Deeper learning — Signals effectively propagate through deep networks, which allows for learning in otherwise untrainable networks. ReZero successfully trains 10,000 layers of fully-connected networks, and we are the first to train Transformers over 100 layers without learning rate warm-up or LayerNorm. In contrast to [11] we find that to get good results at this depth, it is not necessary to add auxiliary losses.
Faster convergence — We observe significantly accelerated convergence in ReZero networks com- pared to regular residual networks with normalization. When ReZero is applied to Transformers, we converge 56% faster than the vanilla Transformer to reach 1.2 BPB on the enwiki8 language modeling benchmark. When applied to ResNets, we obtain 32% speed up to reach 85% accuracy on CIFAR 10.
ReZero具有两个主要优点:
深度学习-信号通过深度网络有效传播,从而可以在原本无法训练的网络中学习。 ReZero成功地训练了10,000层的全连接网络,并且我们是第一个训练100层以上的互感器而无需学习速率预热或LayerNorm的公司。 与[11]相比,我们发现要在此深度获得良好的结果,没有必要增加辅助损耗。
更快的收敛—与正规化的残留网络相比,ReZero网络的收敛明显加快。 当ReZero应用于Transformers时,在enwiki8语言建模基准上,我们的收敛速度比普通Transformer快56%,达到1.2 BPB。 当应用于ResNets时,在CIFAR 10上,我们可以达到32%的速度,达到85%的精度。
2 Background and related work
Networks with a depth of L layers and width w often have an expressive power that scales expo- nentially in depth, but not in width [12, 5]. Large depth often comes with difficulty in training via gradient-based methods. During training of a deep model, a signal in the training data has to propagate forward from the input to the output layer, and subsequently, the cost function gradients have to propagate backwards in order to provide a meaningful weight update. If the magnitude of a perturbation is changed by a factor r in each layer, both signals and gradients vanish or explode at a rate of rL, rendering many deep networks untrainable in practice.
深度为L层且宽度为w的网络通常具有表示能力,其表达能力在深度而不是宽度上呈指数比例缩放[12,5]。 大深度通常难以通过基于梯度的方法进行训练。 在深度模型训练期间,训练数据中的信号必须从输入向前传播到输出层,随后,成本函数梯度必须向后传播以便提供有意义的权重更新。 如果在每一层中扰动的幅度都被改变了r,则信号和梯度都将以rL的速率消失或爆炸,从而使许多深层网络在实践中无法训练。
There have been many attempts to improve signal propagation through deep networks, and they often fall into one of three categories — initialization schemes, normalization layers, and residual connections. We show some of the popular ways to combine residual networks with normalization in Table 1.
已经进行了许多尝试来改善通过深度网络的信号传播,并且它们通常属于三类之一-初始化方案,归一化层和残余连接。 我们在表1中显示了一些将残差网络与规范化相结合的流行方法。
2.1 Careful initialization
In recent years the dynamics of signal propagation in randomly initialized deep and wide neural networks have been formalized via mean field theory [13, 8, 14]. For some deep neural networks, including fully connected and convolutional architectures, the cosine distance of two distinct signals,
近年来,通过均场理论[13,8,14]形式化了随机初始化的深层和宽层神经网络中信号传播的动力学。 对于某些深层神经网络,包括全连接和卷积架构,两个不同信号的余弦距离
approaches a fixed point that either vanishes or approaches unity at large depths. If this fixed point is 1 the behavior of the network is stable and every input is mapped to the same output, leading to vanishing weight updates. If this fixed point is 0 the behavior of the network is chaotic and even similar inputs are mapped to very different outputs, leading to exploding weight updates. To understand whether a network is in a stable or chaotic phase we consider the input-output Jacobian
接近在大深度处消失或接近统一的固定点。 如果此固定点为1,则网络的行为是稳定的,并且每个输入都映射到相同的输出,从而导致权重更新消失。 如果此固定点为0,则网络的行为将变得混乱,甚至将相似的输入映射到非常不同的输出,从而导致权重更新呈爆炸式增长。 为了了解网络是处于稳定阶段还是混沌阶段,我们考虑输入输出雅可比矩阵
The mean squared singular values χ of this matrix determine the growth/decay of an average input signal perturbation as it propagates through the network. The network exhibits a boundary between the ordered and the chaotic phase, the edge of chaos at χ = 1. Training proceeds efficiently at the edge of chaos.
This behavior was recognized in [15, 6], which motivated a re-scaling of the weights such that χ ≈ 1 and on average signal strengths are neither enhanced or attenuated.
Pennigton et al. [13, 14] recognized that a unit mean squared average of the input-output Jacobian is insufficient to guarantee trainability. For example, if the singular vectors of Jio corresponding to very large/small singular values align well with the perturbations in the data, training will still be inefficient. They proposed the stronger condition of dynamical isometry [16], which requires that all singular values of Jio are close to one. This means that all perturbations of the input signal propagate through the network equally well. The ReLU activation function maps to zero for some perturbations of the input signal, and it is therefore intuitive that deep networks with ReLU activations cannot possibly satisfy dynamical isometry, as was rigorously established in [13]. For some activation functions and network architectures, elaborate initialization schemes allow the network to satisfy dynamical isometry at initialization, which significantly improves training dynamics [17, 5, 18, 19].
该矩阵的均方平方奇异值χ确定平均输入信号扰动在网络中传播时的增长/衰减。网络在有序和混沌阶段之间表现出边界,即χ= 1处的混沌边缘。训练在混沌边缘有效地进行。
这种行为在[15,6]中得到了认可,它促使权重的重新调整,使得χ≈1和平均信号强度均未增强或减弱。
Pennigton等。 [13,14]认识到输入输出雅可比矩阵的均方根平均值不足以保证可训练性。例如,如果对应于非常大/小的奇异值的Jio奇异矢量与数据中的扰动很好地对齐,则训练仍将是低效的。他们提出了动态等距的更强条件[16],它要求Jio的所有奇异值都接近1。这意味着输入信号的所有扰动均会很好地通过网络传播。对于输入信号的某些扰动,ReLU激活函数映射为零,因此很直观地发现,具有ReLU激活的深层网络可能无法满足动态等距,正如在[13]中严格建立的那样。对于某些激活功能和网络体系结构,精心设计的初始化方案允许网络在初始化时满足动态等距图,从而显着提高训练动态性[17、5、18、19]。
2.2 Normalization
An alternative approach to improve the trainability of deep neural networks is to incorporate layers that explicitly provide normalization. Many normalization modules have been proposed, with the two most popular ones being BatchNorm [9] and LayerNorm [10]. In general, normalization aims to ensure that initially, signals have zero mean and unit variance as they propagate through a network, reducing “covariate shift” [9]. For simplicity we will focus primarily on comparisons against LayerNorm because BatchNorm has additional regularizing effects that are orthogonal to our investigation.
Normalization methods have shown success in accelerating the training of deep networks, but they do incur a computational cost to the network and pose additional hyperparameters to tune (e.g., where to place the normalization). In contrast to normalization methods, our proposed method is simple and cheap to implement. ReZero alone is sufficient to train deeper networks, even in the absence of various norms. Although ReZero makes normalization superfluous for convergence, we have found the regularizing effect of BatchNorm to be complementary to our approach.
改善深度神经网络的可训练性的另一种方法是合并显式提供标准化的层。已经提出了许多规范化模块,其中两个最受欢迎的模块是BatchNorm [9]和LayerNorm [10]。一般而言,归一化旨在确保信号在通过网络传播时最初具有零均值和单位方差,从而减少“协变量偏移” [9]。为简单起见,我们将主要关注与LayerNorm的比较,因为BatchNorm具有与我们的研究正交的其他正则化效果。
规范化方法在加速深度网络的训练方面已显示出成功,但是它们确实会给网络带来计算成本,并带来其他超参数进行调整(例如,将规范化放在何处)。与归一化方法相比,我们提出的方法简单且实现成本低。即使没有各种规范,仅ReZero即可训练更深的网络。尽管ReZero使归一化对于收敛是多余的,但我们发现BatchNorm的正则化效果与我们的方法互补。
2.3 Residual connections
The identity mappings introduced in [2] enabled a deep residual learning framework in the context of convolutional networks for image recognition that significantly increased the trainable depth. The complementary use of BatchNorm and ResNets [2] has enabled the training of convolutional neural networks with over 100 layers. The same has not been the case for LayerNorm and Transformer architectures. Yang et al. [18] studied residual fully connected networks and demonstrated that due to the skip connection, signals decay more slowly (polynomially) as they propagate, allowing for effective training of deeper networks.
Concurrently with our work SkipInit [20], an alternative to the BatchNorm, was proposed for ResNet architectures that is similar to ReZero. The authors find that in deep ResNets without BatchNorm, a scalar multiplier is needed to ensure convergence. We arrive at a similar conclusion for the specific case considered in [20], and study more generally signal propagation in deeper networks across multiple architectures and beyond BatchNorm.
在[2]中引入的身份映射在卷积网络的背景下为图像识别提供了一个深度残差学习框架,极大地增加了可训练的深度。 BatchNorm和ResNets [2]的互补使用使训练具有100多个层的卷积神经网络成为可能。对于LayerNorm和Transformer体系结构,情况并非如此。杨等。 [18]研究了残余的全连接网络,并证明由于跳过连接,信号在传播时衰减较慢(多项式),从而可以对较深的网络进行有效的训练。
与我们的工作同时进行的是SkipInit [20],它是与ReZero类似的ResNet体系结构的BatchNorm的替代方案。作者发现,在没有BatchNorm的深层ResNet中,需要一个标量乘数来确保收敛。对于[20]中考虑的特定案例,我们得出了相似的结论,并且更广泛地研究了跨多个架构以及BatchNorm的更深网络中的信号传播。
3 ReZero
We propose ReZero (residual with zero initialization), a simple change to the architecture of deep residual networks that facilitates dynamical isometry and enables the efficient training of extremely deep networks. Rather than propagating the signal through each of the non-trivial functions F[Wi] at initialization, we add a skip connection and rescale the function by L learnable parameters αi (which we call residual weights) that are initialized to zero. The signal now propagates according to
我们提出了ReZero(零归零残差),它是对深残差网络体系结构的简单更改,可促进动态等距并实现对极深网络的有效训练。 与其在初始化时通过每个非平凡函数F [Wi]传播信号,不如添加一个跳过连接并通过初始化为零的L个可学习参数αi(我们称为残权)来重新缩放该函数。 现在,信号根据
At initialization the network represents the identity function and it trivially satisfies dynamical
isometry. We demonstrate below for a toy model that this architecture can exponentially accelerate training. The architecture modification allows for the training of deep networks even when the individual layers’ Jacobian has vanishing singular values, as is the case for ReLU activation functions or self-attention [21]. The technique also allows us to add arbitrary new layers to existing and trained networks.
在初始化时,网络代表身份功能,并且可以轻松满足动态需求
等轴测图。 我们在下面的玩具模型中演示该架构可以成倍地加快训练速度。 架构修改允许即使在各个层的Jacobian值都消失了的情况下也可以训练深度网络,例如ReLU激活功能或自我注意[21]。 该技术还允许我们向现有和经过培训的网络添加任意新层。

Figure 2: Contour log plots of a quadratic cost function (left) and gradient norm (right) over the network weight w and the residual weight α during the training of the linear function xL = 5x0 via gradient descent using a training set of x0 = {1, 2, 3}. Gradient descent trajectories initialized at α = 0 are shown in red for five different initial w’s. The trajectory dynamics avoid the poorly conditioned regions around α ≈ 1.
图2:在线性权重xL = 5x0的训练中,使用x0 =的训练集对网络权重w和剩余权重α进行二次代价函数(左)和梯度范数(右)的轮廓对数图 {1,2,3}。 对于五个不同的初始w,以α= 0初始化的梯度下降轨迹以红色显示。 轨迹动力学避免了α≈1附近条件差的区域。
3.1 A toy example
To illustrate how the ReZero connection accelerates training let us consider the toy model of a deep neural network described by L single-neuron hidden layers that have no bias and all share the same weight w and αi = α ∀i. The network then simply maps an input x0 to the output
为了说明ReZero连接如何加快训练速度,让我们考虑由L个单神经元隐藏层描述的深度神经网络的玩具模型,这些隐藏层没有偏倚,并且都具有相同的权重w和αi=α∀i。 然后,网络只需将输入x0映射到输出
![]()
Fixing the parameter α = 1 would represent a toy model for a fully connected residual network, while initializing α = 0 and treating α as a learned parameter corresponds to a ReZero network. The input-output Jacobian is given by Jio = (1 + αw)L, indicating that for initialization with w ≈ 1 and α = 1 the output signal of a deep (i.e., L ≫ 1) network is extremely sensitive to any small perturbations of the input, while with α = 0 the input signal magnitude is preserved. While this example is too simple to exhibit an order/chaos phase transition, it does accurately model the vanishing and exploding gradient problem familiar in deep networks. Assuming a learning rate λ and a cost function C, gradient descent updates the weights w according to
固定参数α= 1将代表完全连接的残差网络的玩具模型,而初始化α= 0并将α作为学习的参数对应于ReZero网络。 输入输出雅可比关系式由Jio =(1 +αw)L给出,表明对于w≈1且α= 1的初始化,深层(即L≫ 1)网络的输出信号对任何小扰动都极为敏感。 当α= 0时,输入信号的幅度得以保留。 尽管此示例过于简单以至于无法表现出阶跃/混沌相变,但它确实可以对深层网络中熟悉的消失和爆炸梯度问题进行精确建模。 假设学习率λ和成本函数C,则梯度下降根据

For α = 1, convergence of gradient descent with an initial weight w ≈ 1 requires steps no larger than
1, and hence a learning rate that is exponentially small in depth L
对于α= 1,初始权重w≈1的梯度下降的收敛要求步长不大于
1,因此学习率在深度L上成倍减小
where we only retained the parametric dependence on w and L. For w ≫ 1 the gradients in Equation 6 explode, while for w ≈ −1 the gradients vanish. Initializing α = 0 solves both of these problems: assuming a sufficiently well-conditioned cost function, the first step of gradient descent will update the residual weights α to a value that avoids large outputs and keeps the parameter trajectory within a well-conditioned region while retaining the expressive power of the network. The first non-trivial steps of the residual weight are given by
在这里,我们只保留了对w和L的参数依赖性。对于w≫ 1,等式6中的梯度会爆炸,而对于w≈-1,梯度会消失。 初始化α= 0解决了这两个问题:假设条件条件条件足够充分,则梯度下降的第一步将把剩余权重α更新为一个避免大输出并将参数轨迹保持在条件范围内的值,而 保留网络的表现力。 剩余权重的第一个非平凡步骤为
and gradient descent will converge with a learning rate that is polynomial in the depth L of the network. In this simple example, the ReZero connection, therefore, allows for convergence with dramatically fewer optimization steps than a vanilla residual network. We illustrate the training dynamics, cost function and gradients in Figure 2.
梯度下降将以网络深度L中多项式的学习速率收敛。 因此,在这个简单的示例中,与原始残差网络相比,ReZero连接允许以更少的优化步骤进行收敛。 我们在图2中说明了训练动态,成本函数和梯度。
4 Training deep fully connected networks faster
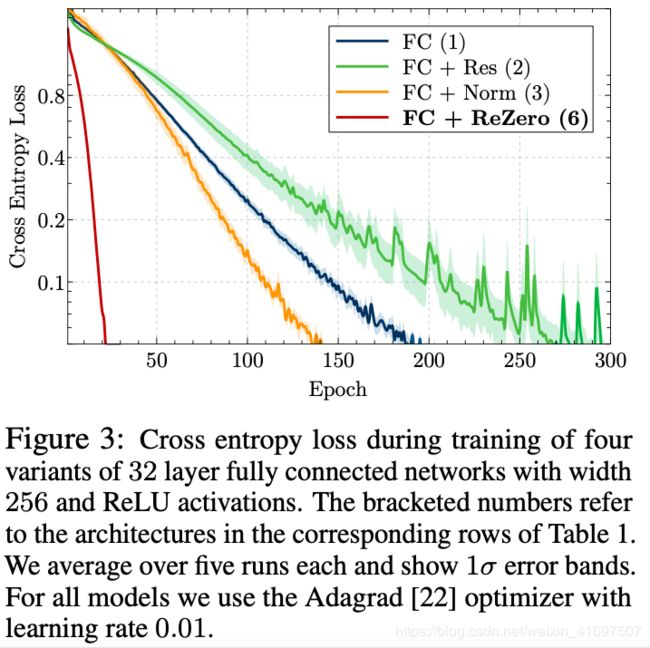
Figure 3: Cross entropy loss during training of four variants of 32 layer fully connected networks with width 256 and ReLU activations. The bracketed numbers refer to the architectures in the corresponding rows of Table 1. We average over five runs each and show 1σ error bands. For all models we use the Adagrad [22] optimizer with learning rate 0.01.
图3:训练宽度为256和ReLU激活的32层完全连接网络的四个变体时的交叉熵损失。 方括号中的数字指的是表1中相应行的体系结构。我们平均进行了5次运行,并显示了1σ误差带。 对于所有模型,我们使用学习率0.01的Adagrad [22]优化器。
As a sample toy task, we train four different net- work architectures on the CIFAR-10 data set for supervised image classification. We are only in- terested in the training dynamics and investigate how many iterations it takes for the model to fit the data.
We show the evolution of the training loss in Figure 3. In our simple experiment, a 32 layer network the ReZero architecture converges to fit the training data between 7 and 15 times faster than the other techniques. Note that without an additional normalization layer the residual connection decreases convergence speed compared to a plain fully connected network. We speculate that this is because at initialization the variance of the signal is not independent of depth, see [18].
With increasing depth, the advantages of the ReZero architecture become more apparent. To verify that this architecture ensures trainability to large depths we successfully trained fully connected ReZero networks with up to 10, 000 layers on a laptop with one GPU3 to overfit the training set.
作为示例玩具任务,我们在CIFAR-10数据集上训练了四种不同的网络体系结构,以进行监督图像分类。我们仅对训练动态感兴趣,并研究了模型拟合数据所需的迭代次数。
我们在图3中显示了训练损失的演变。在我们的简单实验中,ReZero体系结构收敛了一个32层网络,比其他技术快7到15倍来拟合训练数据。请注意,与普通的完全连接网络相比,没有额外的归一化层,剩余连接会降低收敛速度。我们推测这是因为在初始化时信号的方差与深度无关,请参见[18]。
随着深度的增加,ReZero体系结构的优势变得更加明显。为了验证该体系结构确保可深度训练,我们在配备一台GPU3的笔记本电脑上成功训练了多达10、000层的全连接ReZero网络,以适应训练集的要求。
5 Training deeper Transformers faster
In this section, we study the signal propagation and application of ReZero to the Transformer architecture [21]. Transformers gained significant popularity and success both in supervised and unsupervised NLP tasks [23, 11]. Transformers are built by stacking modules that first perform self-attention, then a point- wise feed-forward transformation.
The original Transformer [21] implementation can be seen as a residual network with post-normalization (row 5 in Table 1). Inside a Transformer module the output of each sublayer is added via a residual connection and then normalized by LayerNorm,
在本节中,我们研究ReZero的信号传播及其在Transformer体系结构中的应用[21]。 在有监督和无监督的NLP任务中,变压器都获得了极大的欢迎和成功[23,11]。 变压器由堆叠模块构建,这些模块首先执行自我关注,然后进行逐点前馈转换。
最初的Transformer [21]实现可以看作是具有后归一化功能的残差网络(表1中的第5行)。 在Transformer模块内部,每个子层的输出通过残差连接添加,然后由LayerNorm标准化,
where sublayer ∈ {self-attention, feed-forward}, as
illustrated in the left panel of Figure 4.
5.1 Signal propagation in Transformers
Figure 5: Histograms for log singular values λio of the input-output Jacobian matrix for: (a) Transformer encoder network at initialization of depths 4, 12 and 64 layers; (b) ReZero Transformer encoder network with 64 layers before and during training. Deep Transformers are far from dynamical isometry, λio ≪ 1, while ReZero Transformers remain closer to dynamical isometry with mean singular value λio ≈ 1.
图5:用于以下情况的输入-输出雅可比矩阵的对数奇异值λio的直方图:(a)在深度4、12和64层初始化时的变压器编码器网络; (b)在训练之前和训练期间使用64层的ReZero Transformer编码器网络。 Deep Transformers远离动态等距,λio≪ 1,而ReZero Transformers仍然更接近动态等距,平均奇异值λio≈1。
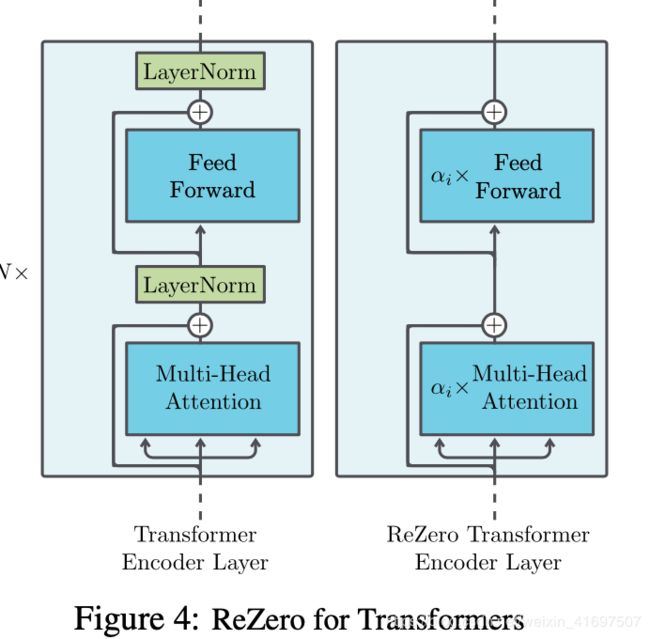
Two crucial components relevant to the signal propagation in the original Transformer layers include LayerNorm [10] and (multi-head) self attention [21]. We will argue that neither component by itself or in conjunction with a vanilla residual connection can satisfy dynamical isometry for all input signals. This finding motivates the use of a ReZero connection to replace both LayerNorm and the vanilla residual connection.
Layer normalization removes the mean and scales the variance over all neurons of a given layer and introduces learnable parameters γ and β to re-scale the variance and shift the mean according to
与原始Transformer层中的信号传播相关的两个关键组件包括LayerNorm [10]和(多头)自我关注[21]。 我们将论证,无论是分量本身还是与香草残差连接相结合,都不能满足所有输入信号的动态等轴测图。 这一发现促使人们使用ReZero连接来替代LayerNorm和香草残余连接。
层归一化去除均值并缩放给定层的所有神经元的方差,并引入可学习的参数γ和β重新缩放方差并根据
It is clear from this definition that perturbing an input x by a transformation that purely shifts either its mean or variance will leave the output unchanged. These perturbations, therefore, give rise to two vanishing singular values of the input-output Jacobian. In the Transformer architecture [21] the norm is applied to each of the n elements of the input sentence, leading to a total of 2 × n vanishing singular values of the Jacobian for each Transformer layer.
从这个定义可以清楚地看出,通过纯粹地移动均值或方差的变换来扰动输入x会使输出保持不变。 因此,这些扰动会导致输入输出Jacobian的两个奇异值消失。 在Transformer体系结构[21]中,将规范应用于输入语句的n个元素中的每个元素,从而导致每个Transformer层的雅可比行列共有2×n消失的奇异值。
In general, the singular value spectrum of the Jacobian of this attention process is complicated. Rather than studying it in full generality, we now merely argue that for some inputs x and weights W Q,K,V the Jacobian has a large number of vanishing singular values (a claim we evaluate empirically below). Consider weights or inputs such that each of the arguments of the softmax function is small compared to 1. The softmax function then simply returns a n × n dimensional matrix filled with entries that all approximate 1/n. This means that the attention function projects all embedding vectors of the input sequence onto a single diagonal direction. This implies that out of the n × d Jacobian singular values only d are non-vanishing and hence much of the input signal is lost. A residual connection can restore some of the lost signals, but even then some perturbations are amplified while others are attenuated. This example demonstrates that self-attention is incompatible with dynamical isometry and unimpeded signal propagation in deep Transformer networks. It is easy to verify that the same conclusion holds for multi-head attention. A careful initialization of the weights might alleviate some of these issues, but we are not aware of any initialization scheme that would render a Transformer layer consistent with dynamical isometry.
通常,该注意力过程的雅可比行列式的奇异值谱很复杂。现在,我们并没有完全全面地研究它,而只是争辩说,对于某些输入x和权重W Q,K,V,雅可比行列式具有大量消失的奇异值(我们在下面的经验中对此求值进行了评估)。考虑权重或输入,以使softmax函数的每个自变量都比1小。softmax函数然后简单地返回一个n×n维矩阵,其中填充了所有近似为1 / n的条目。这意味着注意功能将输入序列的所有嵌入矢量投影到单个对角线方向上。这意味着在n×d雅可比奇异值中,只有d消失,因此很多输入信号丢失。残余连接可以恢复一些丢失的信号,但是即使这样,某些干扰也会放大,而其他干扰则会衰减。此示例说明,在深层变压器网络中,自我注意与动态等距和不受阻碍的信号传播不兼容。容易验证相同的结论对于多头注意力是否成立。权重的仔细初始化可能会缓解其中的一些问题,但是我们不知道有任何初始化方案会使Transformer层与动态等距一致。
We gave a theoretical argument that the vanilla Transformer contains elements that inhibit deep signal propagation. Here, we verify these claims in practice by obtaining the input-output Jacobian for the attention process by evaluating its change under an infinitesimal variation of each of the n × d entries of the input sequence x. We show the input-output Jacobian for Transformer encoder layers of various depth with Xavier uniform initialized weights in Figure 5a. While shallow Transformers exhibit a singular value distribution peaked around unity, we clearly observe that the Jacobian of deep architectures has a large number of singular values that vanish to machine precision. While the distribution varies depending on the details of the initialization scheme, the qualitative statement holds more broadly. These results are consistent with the common observation that deep Transformer networks are extremely challenging to train.
We apply ReZero to solve the problem of poor signal propagation in Transformer layers by replacing LayerNorm and re-scaling the self-attention block. Specifically, this modifies equation (9) to
我们给出了一个理论上的论点,即香草变压器包含的元件会抑制深度信号传播。在这里,我们通过在输入序列x的n×d个条目的无穷小变化下评估其变化来获得注意力过程的输入输出雅可比矩阵,从而在实践中验证这些主张。我们在图5a中显示了具有Xavier统一初始化权重的各种深度的变压器编码器层的输入输出Jacobian值。尽管浅层变压器的奇异值分布在单位附近达到峰值,但我们清楚地观察到,深层架构的雅可比矩阵具有大量奇异值,这些奇异值会消失,从而降低机器的精度。虽然分布取决于初始化方案的详细信息,但定性说明的含义更为广泛。这些结果与普遍的看法一致,即深层变压器网络极难训练。
我们应用ReZero通过替换LayerNorm并重新调整自注意力模块来解决Transformer层中信号传播较差的问题。具体而言,这将等式(9)修改为
where αi is the learned residual weight parameter as in the right panel of Figure 4. We share the same αi parameter for a pair of multi-head self-attention and feed-forward network within a Transformer layer. At initialization, αi = 0, which allows for unimpeded signal propagation: All singular values of the input-output Jacobian are 1 and the model trivially satisfies dynamical isometry. To verify that the model remains close to dynamical isometry throughout training and for larger αi, we show a histogram of the Jacobian singular values during the training of a 64 layer model on a toy task of language modeling on WikiText-2 [24] in Figure 5b. During training the weight of the residual connection gradually increases, allowing the Transformer to model extremely complex functions while maintaining signal propagation properties close to dynamical isometry.
其中,αi是学习的剩余权重参数,如图4的右图所示。我们在变压器层内的一对多头自注意和前馈网络共享相同的αi参数。 在初始化时,αi= 0,这允许无阻碍的信号传播:输入-输出雅可比行列的所有奇异值均为1,并且模型轻松满足动态等距。 为了验证模型在整个训练过程中仍保持与动态等距近似,并且对于较大的αi,我们在WikiText-2上的语言建模玩具任务[64]上显示了一个64层模型的训练过程中,雅可比奇异值的直方图。 5b。 在训练过程中,残余连接的权重逐渐增加,从而使Transformer可以建模极其复杂的功能,同时保持信号传播特性接近动态等距。
5.2 Convergence speed
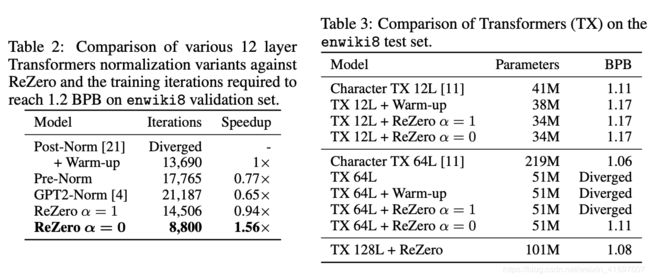
We pick language modeling on enwiki8 [25] as a benchmark because strong language models are a good indicator of downstream NLP task performance [4]. Our aim in these experiments is to measure the convergence speed of each method by measuring the number of iterations it takes for a 12 layer Transformer to reach 1.2 bits per byte (BPB) on enwiki8.
Since the introduction of Transformers [21], there have been several competing placements of the LayerNorm within the Transformer to achieve better convergence [4, 26]. We experiment with 3 Transformer normalization methods and compare against the ReZero Transformer. The Post-Norm (Row 5 in Table 1) method is equivalent to the vanilla Transformer in [21], the Pre-Norm (Row 4 in Table 1) method was recently introduced in [26] and the GPT2-Norm (xi+1 = xi + Norm(F (xi ))) was used in the training of GPT2 [4], which has successfully trained Transformers up to 48 layers. Finally, we experiment with our proposed ReZero method with α initialized to either zero or one. The hyperparameters are in the appendix A.
Our results (Table 2) show that Post-Norm diverges during training while all other models are able to converge. This is not surprising as the original Transformer implementation required a learning rate warm-up and this is also confirmed in [26]. To verify this, we re-ran the Post-Norm setup with 100 steps of learning rate warm-up and find that the model is able to converge to 1.2 BPB in 13,690 iterations. Under this setting, we compared other LayerNorm placements schemes against Post-Norm. We find that the other placements led to initially faster convergence, but ultimately Post-Norm catches up in performance, resulting in relatively slower convergence for Pre-Norm and GPT2-Norm. However, other LayerNorm placements have an advantage over Post-Norm in that they do not require learning rate warm-up, thus have fewer hyperparameters to tune. ReZero with α = 1 does not show an improvement over the vanilla Transformer, indicating the importance of initializing α = 0. With our proposed initialization of α = 0, ReZero converges 56% faster than the vanilla Transformer.
我们选择enwiki8 [25]上的语言建模作为基准,因为强大的语言模型是下游NLP任务性能的良好指标[4]。在这些实验中,我们的目标是通过测量12层Transformer在enwiki8上达到1.2位/字节(BPB)所需的迭代次数来衡量每种方法的收敛速度。
自从引入Transformer [21]以来,在Transformer中存在LayerNorm的多个竞争布局,以实现更好的收敛[4,26]。我们尝试了3种Transformer归一化方法,并与ReZero Transformer进行了比较。后范式(表1中的第5行)方法等同于[21]中的香草变压器,前范式(表1中的第4行)方法最近于[26]中引入,GPT2-范式(xi + 1 = xi + Norm(F(xi)))用于GPT2的训练[4],它已成功训练了多达48层的变压器。最后,我们用建议的ReZero方法进行实验,将α初始化为零或一。超参数在附录A中。
我们的结果(表2)表明,训练后的范数会发散,而所有其他模型都可以收敛。这并不奇怪,因为最初的Transformer实现要求学习率预热,这在[26]中也得到了证实。为了验证这一点,我们重新进行了100次学习率预热的标准后设置,发现该模型能够在13,690次迭代中收敛到1.2 BPB。在此设置下,我们将其他LayerNorm放置方案与Post-Norm进行了比较。我们发现,其他布局最初会导致更快的收敛,但最终No-Norm赶上了性能,导致Pre-Norm和GPT2-Norm的收敛相对较慢。但是,其他LayerNorm放置优于No-Norm,因为它们不需要预热学习率,因此需要调整的超参数更少。 α= 1的ReZero并未显示出优于香草变压器的改善,表明初始化α= 0的重要性。通过我们建议的α= 0的初始化,ReZero的收敛速度比香草变压器快56%。
5.3 Deeper Transformers
Transformer models that achieve state of the art performance in many NLP tasks [23] usually have less than 24 layers. The deepest model as of our work used up to 78 layers [27] and requires 256 GPUs for training. In this section, we will scale beyond hundreds of Transformer layers and still remain trainable on a desktop machine. To examine whether our approach scales to deeper Transformers, we extend our 12 layer ReZero Transformer from Section 5.2 to 64 and 128 layers and compare against the vanilla Transformer (Post-Norm). The hyperparameters are in appendix section B.
Our results (Table 3) indicate that a 12 layer ReZero Transformer attains the same BPB as a regular Transformer after convergence, which shows that we do not lose any representational expressivity in our model by replacing LayerNorm with ReZero. We find that trying to train deep vanilla Transformers lead to either convergence difficulties or slow training times. When scaled to 64 layers, the vanilla Transformer fails to converge even with a warm-up schedule. A ReZero Transformer with initialization of α = 1 diverges, supporting our theoretically motivated initialization at α = 0. The deeper ReZero Transformers are able to attain better performance than the shallower Transformers.
For comparison, we also display results from Character Transformer [11] which had a similar setup for reference. However, Character Transformer uses more parameters and has many additional auxiliary losses to achieve their performance, which is orthogonal to our work. Our 128 layer Transformer achieves similar performance without any intermediate losses, uses half the number of parameters and has larger depth. We did not tune our hyperparameters, and our models can potentially achieve better results with stronger regularization and a learning rate schedule.
在许多NLP任务中达到最先进性能的变压器模型[23]通常少于24层。我们工作中最深的模型最多使用78层[27],并且需要256个GPU进行训练。在本节中,我们将扩展到数百个Transformer层,并且仍然可以在台式机上进行训练。为了检查我们的方法是否可以扩展到更深的变压器,我们将5.2节的12层ReZero变压器扩展到了64层和128层,并与普通变压器(标准后)进行了比较。超参数在附录B中。
我们的结果(表3)表明,在收敛后,一个12层的ReZero变压器与常规变压器具有相同的BPB,这表明通过用ReZero替换LayerNorm,我们在模型中不会失去任何代表性。我们发现尝试训练深层香草变形金刚会导致收敛困难或训练时间缓慢。当缩放到64层时,即使经过预热计划,香草变压器也无法收敛。初始化为α= 1的ReZero变压器发散了,从而支持了我们在α= 0时的理论上的初始化工作。较深的ReZero变压器比较浅的变压器能够获得更好的性能。
为了进行比较,我们还显示了字符转换器[11]的结果,该结果具有类似的设置以供参考。但是,Character Transformer使用更多的参数,并具有许多额外的辅助损耗来实现其性能,这与我们的工作正交。我们的128层变压器实现了类似的性能,而没有任何中间损失,使用了一半参数,并且具有更大的深度。我们没有调整我们的超参数,并且我们的模型可以通过更强的正则化和学习率计划来潜在地获得更好的结果。
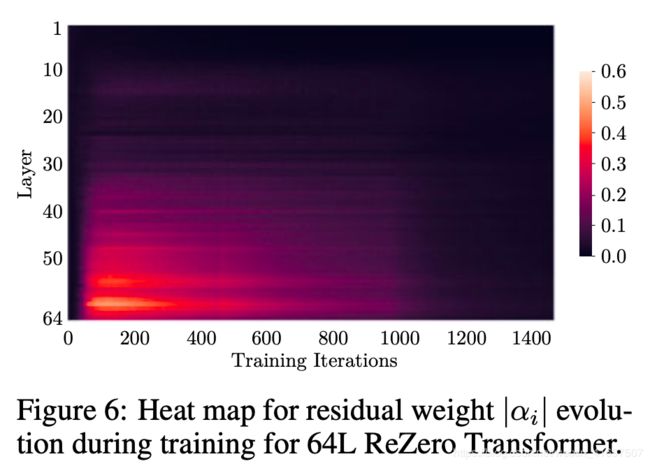
To probe deeper into our model, we examine
the behavior of residual weights αi during train-
ing for our 12 layer and 64 layer ReZero Trans- former (Figure 6). It is useful to view |αi| as the 20 amount of contribution each layer provides to
the overall signal of the network. We see that an
interesting pattern emerges for both the shallow 40
and the deeper ReZero Transformer. During the 50
early iterations of training, the residual weights
quickly increase to a peak value, then slowly
decays to a small value throughout its training.
Early in training, the higher layers tend to be
dominant (they peak earlier) and towards the
end of training each layer is utilized to a similar
degree. The average |αi| at the end of training
is 0.0898 and 0.0185 for the 12 and 64 layer models respectively, which is approximately 1/L, where L is the number of residual layers.
为了更深入地研究我们的模型,我们研究了
列车中剩余权重αi的行为
我们的12层和64层ReZero变压器(图6)。 查看|αi|很有用。 作为每层提供的20个贡献量
网络的整体信号。 我们看到
浅层40都出现了有趣的模式
以及更深的ReZero transformer。 在50年代
训练的早期迭代,剩余权重
快速增加到峰值,然后缓慢增加
在整个训练过程中衰减到很小的值。
在训练的早期,高层往往是
占主导地位(它们较早达到峰值)并向
训练结束后,将每一层都用于相似的
学位。 平均|αi| 在训练结束时
对于12层和64层模型,分别为0.0898和0.0185,约为1 / L,其中L是剩余层数。
Interestingly, this pattern also occurs in the 12 layer ReZero Transformer when we initialized α = 1, except the model spends the first ≈ 50 iterations forcing the α’s to small values, before reaching a similar pattern to that shown in Figure 6. This empirical finding supports our proposal that we should initialize α = 0 even for shallow models.
有趣的是,当我们初始化α= 1时,这种模式也会出现在12层ReZero Transformer中,除了在达到与图6所示模式相似的模式之前,该模型先进行了约50次迭代,将α强制为较小的值。 支持我们的建议,即使对于较浅的模型,我们也应初始化α= 0。
6 Training ResNets faster
In the previous sections, we saw how ReZero connections enable training of deep networks that con- tain layers with vanishing Jacobian singular values, such as ReLU activations or self-attention. Some of these architectures are not trainable without ReZero connections or other architectural changes. In this section, we apply ReZero connections to deep residual networks for image recognition [2]. While these networks are trainable without ReZero connections, we observe that the validation error for a ResNet56 model4 trained (up to 200 epochs) on the CIFAR-10 dataset improves significantly —
from (7.37 ± 0.06)% to (6.46 ± 0.05)% — after trading all vanilla residual connections in the model 5
for ReZero connections . The number of epochs to decrease the validation error below 15% also dropped by (32 ± 14)% after implementing ReZero. While these results provide only limited insight by themselves, they point towards broader applicability of ReZero connections and motivate further study.
在前面的部分中,我们看到了ReZero连接如何使深层网络训练成为可能,这些深层网络包含具有消失的Jacobian奇异值(例如ReLU激活或自我注意)的层。如果没有ReZero连接或其他架构更改,其中某些架构将无法训练。在本节中,我们将ReZero连接应用于深层残差网络以进行图像识别[2]。尽管这些网络无需ReZero连接即可进行训练,但我们观察到,在CIFAR-10数据集上训练的ResNet56 model4(最多200个纪元)的验证错误得到了显着改善-
从(7.37±0.06)%到(6.46±0.05)%-在交易了模型5中的所有香草残余连接之后
用于ReZero连接。在实施ReZero之后,将验证误差降低到15%以下的时期数也减少了(32±14)%。尽管这些结果本身仅提供了有限的见识,但它们指出了ReZero连接的更广泛的适用性,并激发了进一步的研究。
7 Conclusion
We introduced ReZero, a simple architecture modification that facilitates signal propagation in deep networks and helps the network maintain dynamical isometry. Applying ReZero to various residual architectures – fully connected networks, Transformers and ResNets – we observed significantly improved convergence speeds. Furthermore, we were able to efficiently train Transformers with hundreds of layers, which has been difficult with the original architecture. We believe deeper Transformers will open doors for future exploration.
While training models with ReZero, we discovered interesting patterns in the values of residual weights of each layer |αi| over the course of training. These patterns may hint towards some form of curriculum learning and allow for progressive stacking of layers to further accelerate training [28]. Patterns of residual weights can be crucial to understand the training dynamics of such deeper networks and might be important to model performance, which we will explore in future work.
我们推出了ReZero,这是一种简单的体系结构修改,可促进深度网络中的信号传播并帮助网络保持动态等距。将ReZero应用于各种残差架构(完全连接的网络,变压器和ResNets)后,我们发现收敛速度显着提高。此外,我们能够有效地训练数百个层的变压器,这对于原始体系结构来说是困难的。我们相信,更深的变形金刚将为未来的探索敞开大门。
在使用ReZero训练模型时,我们发现了每个图层|αi|的剩余权重值中有趣的模式。在培训过程中。这些模式可能暗示了某种形式的课程学习,并允许逐步堆叠层次以进一步加速培训[28]。剩余权重的模式对于理解这种更深层网络的训练动态至关重要,对模型化性能也可能很重要,我们将在以后的工作中进行探讨。
Acknowledgements
The work of TB was supported in part by DOE under grants no. DE-SC0009919 and by the Simons Foundation SFARI 560536. The work of BPM and HHM was supported by Amazon via the grant of Alexa Prize Grand Challenge 3.
结核病的工作部分由美国能源部(DOE)提供了部分资助。 DE-SC0009919和Simons基金会SFARI560536。BPM和HHM的工作由亚马逊通过Alexa大奖大挑战3的资助而得到了支持。
References
[1] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. nature, 521(7553):436–444, 2015.
[2] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
[3] Günter Klambauer, Thomas Unterthiner, Andreas Mayr, and Sepp Hochreiter. Self-normalizing neural networks. In Advances in neural information processing systems, pages 971–980, 2017.
[4] Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language models are unsupervised multitask learners. OpenAI Blog, 1(8):9, 2019.
[5] Ben Poole, Subhaneil Lahiri, Maithra Raghu, Jascha Sohl-Dickstein, and Surya Ganguli. Exponential expressivity in deep neural networks through transient chaos. In Advances in neural information processing systems, pages 3360–3368, 2016.
[6] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision, pages 1026–1034, 2015.
[7] Dmytro Mishkin and Jiri Matas. All you need is a good init. arXiv preprint arXiv:1511.06422, 2015.
[8] Lechao Xiao, Yasaman Bahri, Jascha Sohl-Dickstein, Samuel S Schoenholz, and Jeffrey Pen- nington. Dynamical isometry and a mean field theory of cnns: How to train 10,000-layer vanilla convolutional neural networks. arXiv preprint arXiv:1806.05393, 2018.
4For our experiments we used the implementation by Yerlan Idelbayev (available at github.com/ akamaster/pytorch_resnet_cifar10) that very closely resembles the original architecture [2].
5Our setup differs from the SkipInit proposal in [20], in that we retain the BatchNorm layer. 9
[9] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167, 2015.
[10] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization. arXiv preprint arXiv:1607.06450, 2016.
[11] Rami Al-Rfou, Dokook Choe, Noah Constant, Mandy Guo, and Llion Jones. Character-level language modeling with deeper self-attention. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 3159–3166, 2019.
[12] Guido F Montufar, Razvan Pascanu, Kyunghyun Cho, and Yoshua Bengio. On the number of linear regions of deep neural networks. In Advances in neural information processing systems, pages 2924–2932, 2014.
[13] Jeffrey Pennington, Samuel Schoenholz, and Surya Ganguli. Resurrecting the sigmoid in deep learning through dynamical isometry: theory and practice. In Advances in neural information processing systems, pages 4785–4795, 2017.
[14] Jeffrey Pennington, Samuel S Schoenholz, and Surya Ganguli. The emergence of spectral universality in deep networks. arXiv preprint arXiv:1802.09979, 2018.
[15] Xavier Glorot and Yoshua Bengio. Understanding the difficulty of training deep feedfor- ward neural networks. In Proceedings of the thirteenth international conference on artificial intelligence and statistics, pages 249–256, 2010.
[16] Andrew M Saxe, James L McClelland, and Surya Ganguli. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv preprint arXiv:1312.6120, 2013.
[17] Samuel S Schoenholz, Justin Gilmer, Surya Ganguli, and Jascha Sohl-Dickstein. Deep informa- tion propagation. arXiv preprint arXiv:1611.01232, 2016.
[18] Ge Yang and Samuel Schoenholz. Mean field residual networks: On the edge of chaos. In Advances in neural information processing systems, pages 7103–7114, 2017.
[19] Dar Gilboa, Bo Chang, Minmin Chen, Greg Yang, Samuel S Schoenholz, Ed H Chi, and Jeffrey Pennington. Dynamical isometry and a mean field theory of lstms and grus. arXiv preprint arXiv:1901.08987, 2019.
[20] Soham De and Samuel L Smith. Batch normalization biases deep residual networks towards shallow paths. arXiv preprint arXiv:2002.10444, 2020.
[21] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems, pages 5998–6008, 2017.
[22] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of machine learning research, 12(Jul):2121–2159, 2011.
[23] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: pre-training of deep bidirectional transformers for language understanding. In Jill Burstein, Christy Doran, and Thamar Solorio, editors, NAACL, pages 4171–4186, 2019.
[24] Stephen Merity, Caiming Xiong, James Bradbury, and Richard Socher. Pointer sentinel mixture models. In ICLR, 2017.
[25] Matt Mahoney. Large text compression benchmark, 2009.
[26] Ruibin Xiong, Yunchang Yang, Di He, Kai Zheng, Shuxin Zheng, Chen Xing, Huishuai Zhang, Yanyan Lan, Liwei Wang, and Tie-Yan Liu. On layer normalization in the transformer architecture. arXiv preprint arXiv:2002.04745, 2020.
[27] Microsoft. Turing-nlg: A 17-billion-parameter language model, 2020. 10
[28] Linyuan Gong, Di He, Zhuohan Li, Tao Qin, Liwei Wang, and Tie-Yan Liu. Efficient training of BERT by progressively stacking. In Kamalika Chaudhuri and Ruslan Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA, volume 97 of Proceedings of Machine Learning Research, pages 2337–2346. PMLR, 2019.
[29] Dan Hendrycks and Kevin Gimpel. Bridging nonlinearities and stochastic regularizers with gaussian error linear units. CoRR, abs/1606.08415, 2016.
[30] YangYou,JingLi,JonathanHseu,XiaodanSong,JamesDemmel,andCho-JuiHsieh.Reducing BERT pre-training time from 3 days to 76 minutes. CoRR, abs/1904.00962, 2019.
A Convergence speed experimental hyperparameters
For all model variants in Section 5.2, we control the batch size to be 1080, number of layers to 12, feed-forward and attention dropout to 20%, hidden and embedding size to 512 units, context length to 512, the attention heads to 2, and GELU [29] activation in the point-wise feed-forward layer. To accommodate large batch training we use the LAMB optimizer [30] with a fixed learning rate of 0.016. Although learning rate schedules tend to improve performance [23], we omit them to simplify our training process.
对于第5.2节中的所有模型变体,我们将批量大小控制为1080,层数为12,前馈和注意力下降为20%,隐藏和嵌入的大小为512个单位,上下文长度为512,注意量为 2,并在逐点前馈层激活GELU [29]。 为了适应大批量培训,我们使用LAMB优化器[30],其固定学习率为0.016。 尽管学习率表可以提高绩效[23],但我们省略了它们以简化培训过程。
B Deep Transformers experimental hyperparameters
In Section 5.3, in order to examine whether our approach scales to deeper Transformers, we scale our 12 layer ReZero Transformer from Section 5.2 to 64 layers and 128 layers and compare it against the vanilla Transformer (Post-Norm). Due to memory constraints, we decreased the hidden size from 512 to 256 and reduced batch size to 304 and 144 for the 64 layer and 128 layer model respectively. Following guidelines from [30] we also adjusted the learning rate to according to
在5.3节中,为了检查我们的方法是否可以扩展到更深的变压器,我们将5.2节中的12层ReZero变压器缩放为64层和128层,并将其与香草变压器(标准后)进行比较。 由于内存的限制,对于64层和128层模型,我们将隐藏大小从512减少到256,并将批处理大小分别减少到304和144。 根据[30]的指南,我们还根据
![]()
For all models in our experiments we limit training to a maximum of 100 training epochs.