线段树的设计思路和基本实现
文章目录
- 线段树是个啥?
- 如何创建一个线段树
- 数组空间的大小分配
- 线段树的初始化:buildSegementTree 操作
- 工具类 Merge 操作扩大线段树的使用范围
- 线段树的基础代码
- 测试线段树的方法
- 线段树的查询:Query 操作
- 线段树的更新:Update 操作
线段树是个啥?
在平常见到的树形数据结构中,操作对象都是单个元素,像二分搜索树……;假设要对一个区间进行操作(比如求某个子区间的和),可以使用数组来表示区间,直接对数组进行操作,明显缺点就是时间复杂度过高;这里可以将一个区间拆分为一个个子区间,所有的区间作为二叉树的结点,这颗二叉树是一颗平衡二叉树,即线段树。
如将区间 {1, 5, 3, 9, 12, 7, 15, 10} 存入线段树中,它得树形结构如下:
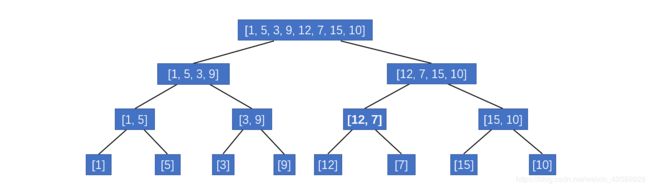
在逻辑上,线段树的每一个结点的确都是区间,但是在物理存储上,线段树中无须存放区间(这样会增加内存的开销),只需要存放我们想要的区间操作结果即可。
线段树的操作一般不会涉及到在区间中动态添加元素的问题,所以使用树的顺序存储形式是比较好的。
如何创建一个线段树
线段树不会在结点中存放区间,那么就需要一个单独的数组来存放这个区间,同时,需要记住我们所有的操作都是基于区间的。
数组空间的大小分配
存放区间的数组空间是固定的,这里需要注意存放树结点的数组空间大小,首先需要了解二叉树的两个性质:
性质1:在二叉树的第 i 层至多有 2 i-1 个结点(i >= 1)
性质2:深度为 k 的二叉树至多有 2 k - 1 个结点(k >= 1)
假设满二叉树的高度为 n + 1,则前 n 层有 2 n -1 个结点,第 n + 1 层 有 2 n 个结点
结论: 满二叉树的第 n 层的结点数目大致等于 前 n-1 层的结点数目。
线段树不一定是满二叉树,但是用满二叉树的空间绝对好使:
- 当区间的大小为 n(n % 2 == 0) 时,此时的线段树是一颗满二叉树,分配 2n 个空间就好使
- 当区间的大小为 n + 1 (n % 2 != 0)时,此时的线段树不是满二叉树;同时,线段树是一颗平衡二叉树,所以结点为单个元素的区间之间的高度差不会超过 1 ,也就是说,在满二叉树的基础上再分配一层的空间绝对够使,所以分配 4n 个空间。
线段树的初始化:buildSegementTree 操作
将一个区间划分为若干子区间时,采用的是等分操作,如下:

那么,我们是如何在树中找到区间呢?
此处,我们利用每一个区间上下边界的中间值 mid ,来划分左孩子和右孩子中的区间范围:
- 左孩子区间范围为[ 0, mid ]
- 右孩子区间范围为[ mid+1, data.length]
通过上面的划分策略,很容易能看出来,线段树其实也是一颗二分搜索树。
工具类 Merge 操作扩大线段树的使用范围
Merge工具类使用方法类似于 Comparator 的使用,我们只需要在实现 Merge 接口的类中重写一个方法,该方法中规定了对区间进行操作的规则,比如:区间求和、求最大值等,操作结果会存入线段树中。
public interface Merge<E> {
E merge(E argument1, E argument2);
}
线段树的基础代码
public class SegementTree<E> {
E[] data; //data用来存储区间中的元素
E[] tree; //tree用来存储线段树中结点
Merge<E> merge;
public SegementTree(E[] arr, Merge<E> merge) {
this.merge = merge;
data =(E[]) new Object[arr.length];
for(int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
if(arr.length % 2 == 0)
tree = (E[]) new Object[arr.length * 2];
else
tree = (E[]) new Object[arr.length * 4];
buildSegementTree(0, 0, data.length-1);
}
public int getSize() {
return data.length;
}
public E get(int idx) {
if(idx < 0 || idx >= data.length) {
throw new IllegalArgumentException("Illegal Idx");
}
return data[idx];
}
private void buildSegementTree(int treeIdx, int l, int r) {
if(l == r) {
tree[treeIdx] = data[l];
return;
}
int mid = l + (r - l)/2;
buildSegementTree(leftChild(treeIdx), l, mid);
buildSegementTree(rightChild(treeIdx), mid+1, r);
tree[treeIdx] = merge.merge(tree[leftChild(treeIdx)], tree[rightChild(treeIdx)]);
}
//获得左孩子的索引值
private int leftChild(int idx) {
return idx * 2 + 1;
}
//获得右孩子的索引值
private int rightChild(int idx) {
return idx * 2 + 2;
}
public String toString() {
StringBuilder str = new StringBuilder();
str.append('[');
for(int i = 0; i < tree.length; i++) {
str.append(tree[i]);
if(i != tree.length - 1)
str.append(',');
}
str.append(']');
return str.toString();
}
}
测试线段树的方法
public class MainTest {
public static void main(String[] args) {
Integer[] arr = new Integer[] {1, 5, 3, 9, 12, 7, 15, 10};
SegementTree<Integer> segement = new SegementTree<>(arr, new Merge<Integer>() {
@Override
public Integer merge(Integer argument1, Integer argument2) {
return argument1+argument2;
}
});
System.out.println(segement);
}
}
Tip: 在使用构造器时,需要传入一个 Merge 类的实例对象(这里叫它融合器),融合器中定义了操作的规则。
线段树的查询:Query 操作
假设查询区间 [2, 5] 的和,实现算法思路中有三种情况:
第一种,区间全部包含在左子树中,即 右边界是小于等于中间值 mid 的
第二种,区间全部包含在右子树中,即 左边界是大于中间值 mid 的
第三种,就是例中的区间包含在左子树和右子树中

public E query(int idxL, int idxR) {
return query(0, idxL, idxR, 0, data.length-1);
}
private E query(int treeIdx, int idxL, int idxR, int l, int r) {
if(idxL == l && idxR == r) {
return tree[treeIdx];
}
int mid = l + (r-l)/2;
if(idxL > mid)
return query(rightChild(treeIdx), idxL, idxR, mid+1, r);
if(idxR <= mid)
return query(leftChild(treeIdx), idxL, idxR, l, mid);
E leftMerge = query(leftChild(treeIdx), idxL, mid, l, mid);
E rightMerge = query(rightChild(treeIdx), mid+1, idxR, mid+1, r);
return merge.merge(leftMerge, rightMerge);
}
线段树的更新:Update 操作
这里的更新操作同样是对区间中元素进行更新,例如将区间中位置为 0 的元素更新为 13:
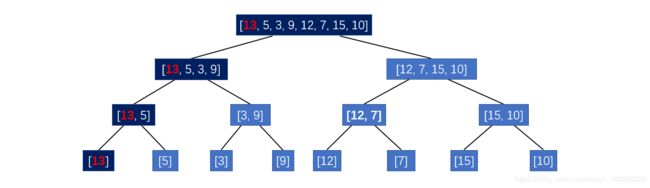
这样,更改一个元素,会引起线段树中包含该元素的所有区间结点都进行更新。
public void update(int idx, E element) {
if(idx < 0 || idx >= data.length) {
throw new IllegalArgumentException("Illegal Idx");
}
data[idx] = element;
updata(0, 0, data.length-1, idx, element);
}
private void updata(int treeIdx, int l, int r, int idx, E element) {
if(l == r) {
tree[treeIdx] = element;
return;
}
int mid = l + (r-l)/2;
if(idx <= mid)
updata(leftChild(treeIdx), l, mid, idx, element);
if(idx > mid)
updata(rightChild(treeIdx), mid+1, r, idx, element);
tree[treeIdx] = merge.merge(tree[leftChild(treeIdx)], tree[rightChild(treeIdx)]);
}