K-Means(K均值)聚类算法的MATLAB实现
最近在学习 k-means聚类算法,网上有很多关于用MATLAB对这一算法的实现,下面对这一知识点进行了总结,希望大家可以采纳,欢迎留言。
在聚类分析中希望能有一种算法能够自动的将相同的元素分为紧密关系的子集或簇。聚类属于无监督学习中的一种方法,也是一种在许多领域中用于统计数据分析的常用技术。K-means算法是使用的最广泛的一种算法。
1.算法步骤:
1)首先选择一些类/组,并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这就需要我们提前预知类的数量(即中心点的数量)。
2)计算每个数据点到中心点的距离,数据点距离哪个中心点最近就划分到哪一类中。
3)计算每一类中中心点作为新的中心点。
4)重复以上步骤,直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点,然后选择运行结果最好的一个。
2.注意事项:
1)K-means中的K表示簇的个数
2)质心:均值,即向量各维度取平均即可。计算距离是使用欧式距离的计算公式:
3)优化目标:,就是使每个样本点到簇心的距离的和最小。
优势:简单、快速、适合常规数据集。
劣势:K值难确定,复杂度与样本呈线性关系。(即样本越多,计算的越多)
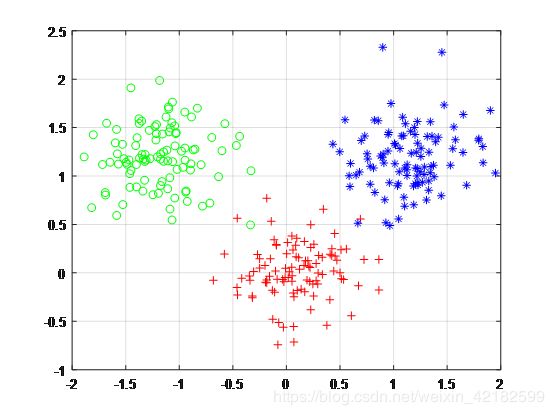
3.用MATLAB实现K-means算法,有三类数据集,设置K=3
clear all;
close all;
clc;
%第一类数据
a=[0 0 ];
S1=[.1 0 ;0 .1];
data1=mvnrnd(a,S1,100); %产生高斯分布数据
%第二类数据
b=[1.2 1.2 ];
S2=[.1 0 ;0 .1];
data2=mvnrnd(b,S2,100);
% 第三类数据
c=[-1.2 1.2 ];
S3=[.1 0 ;0 .1];
data3=mvnrnd(c,S3,100);
%显示数据
plot(data1(:,1),data1(:,2),'r+');
hold on;
plot(data2(:,1),data2(:,2),'b*');
plot(data3(:,1),data3(:,2),'go');
grid on;
%三类数据合成一个不带标号的数据类
data=[data1;data2;data3];
%K-means聚类
N=3;%设置聚类数目
[m,n]=size(data);
re=zeros(m,n+1);
center=zeros(N,n);%初始化聚类中心
re(:,1:n)=data(:,:);
for x=1:N
center(x,:)=data( randi(300,1),:);%第一次随机产生聚类中心
end
while 1
distence=zeros(1,N);
num=zeros(1,N);
new_center=zeros(N,n);
for x=1:m
for y=1:N
distence(y)=norm(data(x,:)-center(y,:));%计算到每个类的距离
end
[~, temp]=min(distence);%求最小的距离
re(x,n+1)=temp;
end
k=0;
for y=1:N
for x=1:m
if re(x,n+1)==y
new_center(y,:)=new_center(y,:)+re(x,1:n);
num(y)=num(y)+1;
end
end
new_center(y,:)=new_center(y,:)/num(y);
if norm(new_center(y,:)-center(y,:))<0.1
k=k+1;
end
end
if k==N
break;
else
center=new_center;
end
end
[m, n]=size(re);
%最后显示聚类后的数据
figure;
hold on;
for i=1:m
if re(i,n)==1
plot(re(i,1),re(i,2),'r+');
plot(center(1,1),center(1,2),'ko');
elseif re(i,n)==2
plot(re(i,1),re(i,2),'b*');
plot(center(2,1),center(2,2),'ko');
elseif re(i,n)==3
plot(re(i,1),re(i,2),'go');
plot(center(3,1),center(3,2),'ko');
else
plot(re(i,1),re(i,2),'m*');
plot(center(4,1),center(4,2),'ko');
end
end
grid on
展示如下:
望可以帮助你们。