多抽样率数字信号处理（ 摘抄）

10.0：序言

     在应用中需要将定抽样率的信号转化为具有不同抽样率的等价信号。例如音频信号常常需要在三种不同速率中进行抽样率的转换。多抽样率数字信号处理系统使用了下抽样和上抽样这两种基本的抽样率器件。以及各种常规期间，如加法器、乘法器及延时器。

      离散时间系统如果在系统多个部分存在不同的抽样率，就称为多抽样率系统。在变抽样率中，基本的抽样速率转换器一定是和低通数字滤波器。

10.1： 基本抽样率转换器件  

    10.1.1 时域特性，

         一个上抽样因子为L的上抽样器，L是正整数，生成的输出序列  是输入序列x[n]的L倍。

                                

       上抽样例子:

clc,clear all,close all
N =input('输入长度=');% 50
L=input('上抽样因子=');% 3
fo=input('输入信号频率='); % 0.12
n=0:N-1;
x=sin(2*pi*fo*n);
%%% y
y=zeros(1,L*length(x));
y([1:L:length(y)])=x; %%% 扩展的关键
figure;
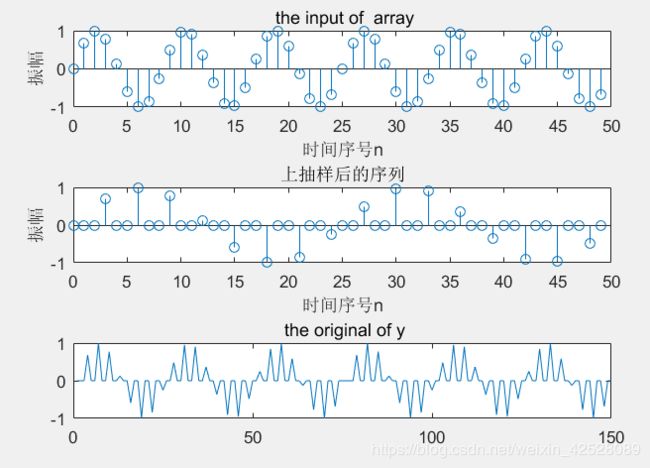
subplot(311); stem(n,x);  title(' the input of  array');  xlabel('时间序号n'),ylabel('振幅');
subplot(312); stem(n,y(1:length(x)));  title('上抽样后的序列');  xlabel('时间序号n'),ylabel('振幅');
subplot(313);plot(y);  title(' the original of y');

生成的图片：

     从图中可以看到，将原始信号x，有50扩展到150，L=3 。但是幅值未发生变化.因此，上抽样器，也称为抽样率扩展器，或者扩展器。

     下抽样器： XI下抽样因子为M 的抽样器，M为正整数，生成的输出序列y[n]的抽样率为输入序列x[n]的1/M 倍。即是每一次抽样保留输入序列中的第M个样本，而除去M-1个样本。

                             

      下抽样例子

clc,clear all,close all;
N =input('输入长度=');% 50
M=input('下抽样因子=');% 3
fo=input('输入信号频率='); % 0.042
n=0:N-1;
m=0:N*M-1;
x=sin(2*pi*fo*m);
%
y=x([1:M:length(x)]);%%% 下采样的关键
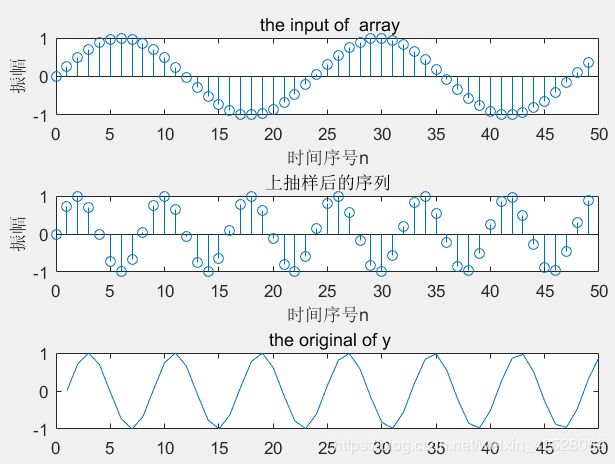
subplot(311); stem(n,x(1:N));  title(' the input of  array');  xlabel('时间序号n'),ylabel('振幅');
subplot(312); stem(n,y);  title('下抽样后的序列');  xlabel('时间序号n'),ylabel('振幅');
subplot(313);plot(y);  title(' the original of y');

生成的图片

      

    在抽样率转换过程中的不同阶段有着各自对应的时间序号。

     

  10.1.2 频域特性

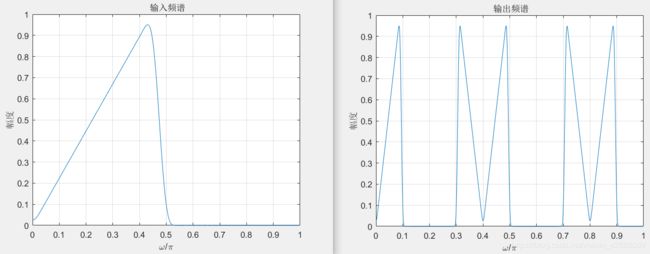
               上抽样后的频谱： 有频谱镜像的效果, 需要使用低通滤波器处理。

clc,clear all,close all;
freq=[0 0.45 0.5 1];
mag=[0 1 0 0];
x=fir2(99,freq,mag);
%%%
figure(1);
[Xz,w]=freqz(x,1,512);
plot(w/pi,abs(Xz));grid 
xlabel('\omega/\pi');ylabel('幅度');
title(' 输入频谱');


L=input('上抽样因子=');% 3
y=zeros(1,L*length(x));
y([1:L:length(y)])=x;
[Yz,w]=freqz(y,1,512);
figure(2);
plot(w/pi,abs(Yz));grid on;
xlabel('\omega/\pi');ylabel('幅度');
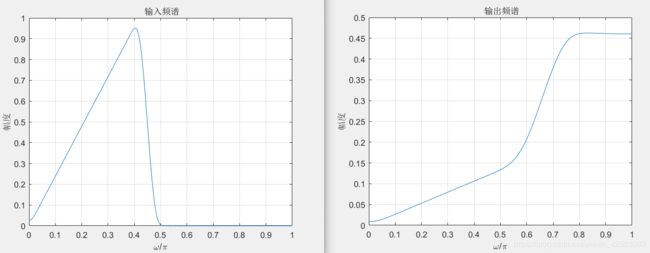
title(' 输出频谱');

          

下抽样后的频谱，容易产生频谱混叠现象.

clc,clear all,close all;
freq=[0 0.42 0.48 1];
mag=[0 1 0 0];
x=fir2(101,freq,mag);
%%%
figure(1);
[Xz,w]=freqz(x,1,512);
plot(w/pi,abs(Xz));grid 
xlabel('\omega/\pi');ylabel('幅度');
title(' 输入频谱');

M=input('下抽样因子=');% 3
y=x([1:M:length(x)]);
[Yz,w]=freqz(y,1,512);
figure(2);
plot(w/pi,abs(Yz));grid on;
xlabel('\omega/\pi');ylabel('幅度');
title(' 输出频谱');

 3 倍 下抽样后的频谱, 占据了整个频谱范围.

10.1.3: 级联等效

       基本的抽样速率转换器只能用一个整数因子改变信号的抽样率，通常需要用到上下抽样率的级联。 在输入和输出不变的前提下，M倍下抽样和L倍上抽样，可相互交换的条件是M 和L 互质。

      上抽样类似于内插，本文的内插初始化值就是0；下抽样类似于取样。

         在实际工程运用中，分数率抽样转换器是不行的。因此常用整数倍数字抽样转换器和”模拟“ 分数率转换器

10.6.1:数字滤波器组

     有共同输入或者输出的一组数字带通滤波器。由分析滤波器组和合成滤波器组组哼。

     分析滤波器组：子滤波器  称为分析滤波器，它用来将输入信号x[n]分解成M 个子带信号 ，每一个子带信号占据原始频带的一部分（窄谱分析）  

    合成滤波器组：一组子带信号  （代表相邻的频带）合成一个信号y[n]。图中显示了一个L带合成滤波器组，每一个滤波器 称为合成滤波器.

     如图所示：

       

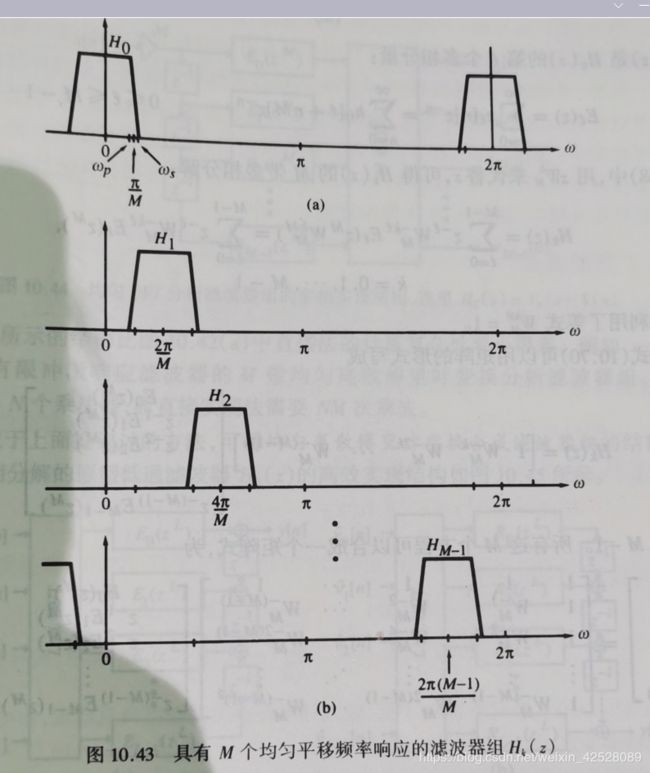
10.6.2: 均匀离散傅里叶变换滤波器组

          滤波器的函数公式:

     

         相应的频率响应

       

         相应的幅度响应

    

        具体如图所示：

        

奈奎斯特滤波器：

     传输函数有一些0值系数 ，这些零值系数是的该类型滤波器的传输效率最高。

 

3：量化误差的来源

      1:滤波器的数值只能取离散值

      2：A/D 或者D/A 之间的转化误差

      3：乘积量化过程的误差