Machine Learning By Andrew Ng (5)
Notes on Machine Learning By Andrew Ng (5)
Click here to see previous note.
Neural Networks: Representation
Non-linear hypotheses
Non-linear classification
You may use polynomial features to find an ideal classifier, but when we have lots of features, it may comes to overfitting in the end.
Neurons and the brain
Model representation I
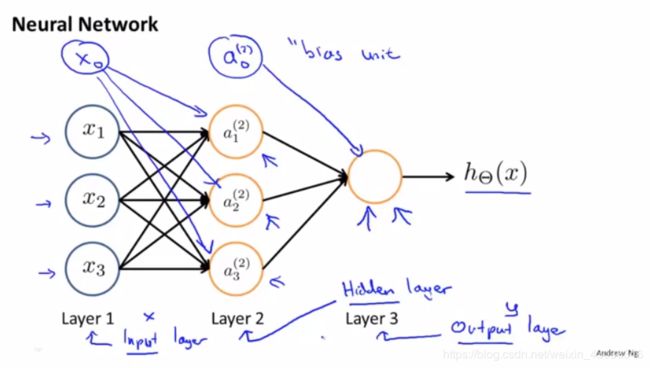
Neuron model: Logistic unit
Notation
a i ( j ) = a_i^{(j)} = ai(j)= “activation” of unit i i i in layer j j j.
$\Theta^{(j)} = $ matrix of weight controlling function mapping from layer j j j to layer j + 1 j+1 j+1.
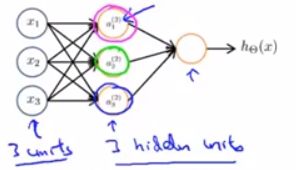
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3)\\ a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3)\\ a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3)\\ h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)hΘ(x)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
If network has s j s_j sj units in layer j j j, s j s_j sj units in layer j + 1 j+1 j+1, then Θ ( j ) \Theta^{(j)} Θ(j) will be of dimension s j + 1 × ( s j + 1 ) s_{j+1} \times (s_j+1) sj+1×(sj+1).
Model representation II
Forward propagation(前向传播): Vertorized implementation
Let Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 = z 1 ( 2 ) \Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3 = z^{(2)}_1 Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3=z1(2) and a 1 ( 2 ) = g ( z 1 ( 2 ) ) a_1^{(2)} = g(z^{(2)}_1) a1(2)=g(z1(2)).
Turn it to a vector!
x = [ x 0 x 1 x 2 x 3 ] z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] , z ( 2 ) = Θ ( 1 ) x ( x = a ( 1 ) ) a ( 2 ) = g ( z ( 2 ) ) . \mathbf{x} = \left[ \begin{matrix} x_0\\ x_1\\ x_2\\ x_3 \end{matrix} \right]\quad \mathbf{z}^{(2)} = \left[ \begin{matrix} z_1^{(2)}\\ z_2^{(2)}\\ z_3^{(2)} \end{matrix} \right],\\ z^{(2)} = \Theta^{(1)}x\quad (x = a^{(1)})\\ a^{(2)} = g(z^{(2)}). x=⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤z(2)=⎣⎢⎡z1(2)z2(2)z3(2)⎦⎥⎤,z(2)=Θ(1)x(x=a(1))a(2)=g(z(2)).
Add a 0 ( 2 ) = 1 a_0^{(2)} =1 a0(2)=1, z ( 3 ) = Θ ( 2 ) a ( 2 ) z^{(3)} = \Theta^{(2)}a^{(2)} z(3)=Θ(2)a(2), h Θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) h_\Theta(x) = a^{(3)} = g(z^{(3)}) hΘ(x)=a(3)=g(z(3)).
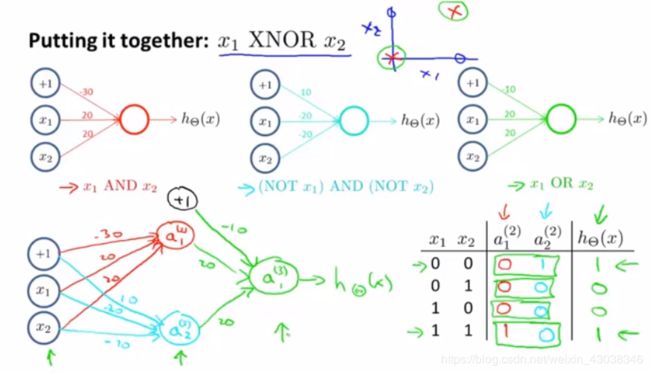
Examples and intuitions I
Examples and intuitions II
Multi-class classification
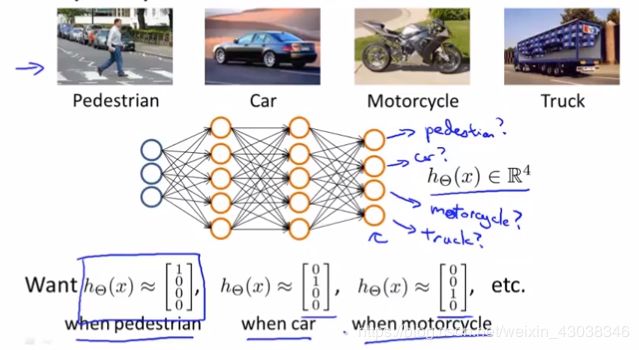
Multiple output units: One-vs-all
Training set: ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ( x ( m ) , y ( m ) ) (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), (x^{(m)}, y^{(m)}) (x(1),y(1)),(x(2),y(2)),(x(m),y(m)),
y ( i ) ∈ [ 1 0 0 0 ] , [ 0 1 0 0 ] , [ 0 0 1 0 ] , [ 0 0 0 1 ] y^{(i)} \in \left[\begin{matrix}1\\0\\0\\0\end{matrix}\right], \left[\begin{matrix}0\\1\\0\\0\end{matrix}\right], \left[\begin{matrix}0\\0\\1\\0\end{matrix}\right],\left[\begin{matrix}0\\0\\0\\1\end{matrix}\right] y(i)∈⎣⎢⎢⎡1000⎦⎥⎥⎤,⎣⎢⎢⎡0100⎦⎥⎥⎤,⎣⎢⎢⎡0010⎦⎥⎥⎤,⎣⎢⎢⎡0001⎦⎥⎥⎤.