禁忌搜索算法实例——TSP
-
算法思想
禁忌搜索算法的两大核心就是渴望水平和禁忌表,即Tabu表。通过禁止之前的产生新解得操作从而避免落入局部最优的概率,同时算法还应有一个渴望水平,也就是迭代过程中最优水平,一旦新解超过最优水平,则能不受Tabu的限制,从而“解禁”。而Tabu表禁止的对象根据实际问题千变万化,这也让该算法在处理离散问题时有了更多的可选项。我们还是以经典NP难问题TSP为例从头编写代码。(MATLAB) -
生成数据
为了方便,我们直接通过randperm来生成一组城市之间的数据,即横纵坐标。
close all;clc;clear;
citys = [randperm(100);randperm(100)]';
- 计算城市距离矩阵D
当我们有了每座城市的横纵坐标时,自然考虑创建[n,n]距离矩阵,二重for循环即可。
n=size(citys,1);
D=zeros(n,n); %D为城市之间距离矩阵
for i=1:n
for j=1:n
if i~=j
D(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));
else
D(i,j)=1e-4;
end
end
end
- 算法的一些初始化
city_size = 100; %城市的个数
x0 = randperm(city_size); %初始线路规划
xbest = x0; %最佳线路规划
dbest = 0;
for i = 1:length(x0)-1
dbest = dbest + D(x0(i),x0(i+1));
end
dbest = dbest + D(x0(end),1); %TSP问题是一个闭环问题
tabu = []; %禁忌表
tabusize = 80; %禁忌表长度限制
iter = 400; %迭代次数上限
A = dbest; %渴望水平
f = dbest; %当前函数值
A_iter = []; %记录渴望水平随迭代次数变化数组
f_iter = []; %记录函数值随迭代次数变化数组
- 下面进入主循环,在这一部分我们采用类似于2-opt的领域移动方式,将路径轨迹的一段倒序即可。具体产生方法如下:
p1 = ceil(city_size*rand(1,2)); %随机1-100中两个整数
p1 = sort(p1);
if(p1(1)~=1)
x1 = [x0(1:p1(1)-1),x0(p1(2):-1:p1(1)),x0(p1(2)+1:end)];
else
x1 = [x0(p1(2):-1:1),x0(p1(2)+1:end)];
end
这里要考虑如果随机到1的话要单独讨论。
- 计算新解和原始解之间的deltas,即距离差。我们为了简单理解,就牺牲了算力,直接for循环。
s1 = 0; %原始解对应的总距离
for i = 1:length(x0)-1
s1 = s1 + D(x0(i),x0(i+1));
end
s1 = s1 + D(x0(end),1);
s2 = 0; %新解对应的总距离
for i = 1:length(x1)-1
s2 = s2 + D(x1(i),x1(i+1));
end
s2 = s2 + D(x1(end),1);
deltaf = s2-s1;
deltas = [deltas,deltaf];
p = [p;p1];
x = [x;x1];
- 下面进入算法核心部分,Tabu更新和f更新以及渴望水平A更新。首先我们要将得到的一系列领域移动结果排个序。
key = 0; %邻域移动方式是否在Tabu表内的标志
[n,m] = sort(deltas); %n是排序结果,m是对应原始索引
p = p(m,:); %p是对应的2-opt方式
x = x(m,:); %x是对应的新解
下面是一系列判断和计算:
for i = 1:length(n)
if(length(tabu)==0)
x0 = x(i,:);
f = f + n(i); %更新函数值
tabu = [tabu;p(i,:)];
if(f+n(i)<A) A = f + n(i); xbest = x0;end
break;
end
if(length(tabu)~=0)
for ii = 1:size(tabu,1)
if(p(i,1)==tabu(ii,1)&&p(i,2)==tabu(ii,2))
key = 1;
break;
end
end
end
if(key==1) %突破渴望水平
if(f+n(i)<A)
x0 = x(i,:);
f = f +n(i);
A = f + n(i);
xbest = x0;
break;
end
end
if(key==0) %新解变动方式不受Tabu表限制
f = f + n(i);
x0 = x(i,:);
tabu = [tabu;p(i,:)];
if(f+n(i)<A) A = f + n(i); xbest = x0;end
break;
end
end
- 禁忌表受Tabu_size限制
这个表长分很多种,例如长期表短期表等等,我们根据实际情况设置为常数即可。下面是更新:
%-----------禁忌表超过tabusize更新-----------%
if(length(tabu)>tabusize)
tabu = tabu(2:end,:);
end
A_iter = [A_iter,A]; %渴望水平变化数组
f_iter = [f_iter,f];
- 结果可视化
disp('最短距离:');
A
disp('最佳路径规划:');
xbest
figure(1);
plot([citys(xbest,1);citys(xbest(1),1)],[citys(xbest,2);citys(xbest(1),2)],'o-');
title('路径规划');
figure(2);
plot(A_iter);
xlabel('迭代次数');
ylabel('渴望水平');
figure(3);
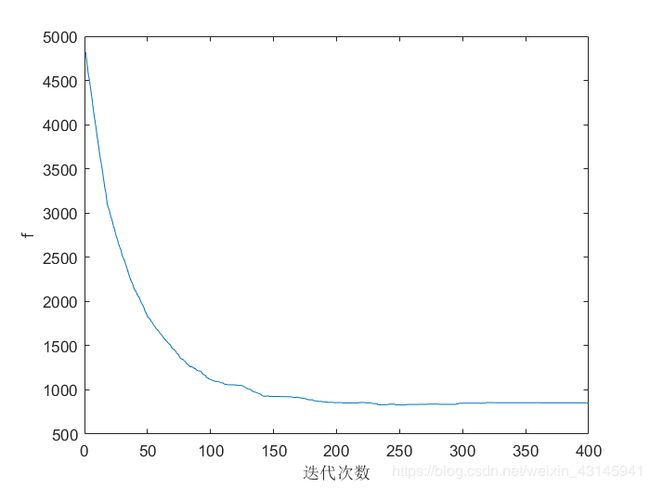
plot(f_iter);
xlabel('迭代次数');
ylabel('f');
- 整体代码
close all;clc;clear;
tic
citys = [randperm(100);randperm(100)]';
n=size(citys,1);
D=zeros(n,n); %D为城市之间距离矩阵
for i=1:n
for j=1:n
if i~=j
D(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));
else
D(i,j)=1e-4;
end
end
end
city_size = 100; %城市的个数
x0 = randperm(city_size); %初始线路规划
xbest = x0; %最佳线路规划
dbest = 0;
for i = 1:length(x0)-1
dbest = dbest + D(x0(i),x0(i+1));
end
dbest = dbest + D(x0(end),1); %TSP问题是一个闭环问题
tabu = []; %禁忌表
tabusize = 80; %禁忌表长度限制
iter = 400; %迭代次数上限
A = dbest; %渴望水平
f = dbest; %当前函数值
A_iter = []; %记录渴望水平随迭代次数变化数组
f_iter = []; %记录函数值随迭代次数变化数组
for k = 1:iter
deltas = []; %距离差
p = []; %记录倒序两个边界序号
x = []; %记录路径
for j = 1:200
p1 = ceil(city_size*rand(1,2)); %随机1-100中两个整数
p1 = sort(p1);
if(p1(1)~=1)
x1 = [x0(1:p1(1)-1),x0(p1(2):-1:p1(1)),x0(p1(2)+1:end)];
else
x1 = [x0(p1(2):-1:1),x0(p1(2)+1:end)];
end
s1 = 0; %原始解对应的总距离
for i = 1:length(x0)-1
s1 = s1 + D(x0(i),x0(i+1));
end
s1 = s1 + D(x0(end),1);
s2 = 0; %新解对应的总距离
for i = 1:length(x1)-1
s2 = s2 + D(x1(i),x1(i+1));
end
s2 = s2 + D(x1(end),1);
deltaf = s2-s1;
deltas = [deltas,deltaf];
p = [p;p1];
x = [x;x1];
end
key = 0;
[n,m] = sort(deltas); %n是排序结果,m是对应原始索引
p = p(m,:);
x = x(m,:);
for i = 1:length(n)
if(length(tabu)==0)
x0 = x(i,:);
f = f + n(i); %更新函数值
tabu = [tabu;p(i,:)];
if(f+n(i)<A) A = f + n(i); xbest = x0;end
break;
end
if(length(tabu)~=0)
for ii = 1:size(tabu,1)
if(p(i,1)==tabu(ii,1)&&p(i,2)==tabu(ii,2))
key = 1;
break;
end
end
end
if(key==1) %突破渴望水平
if(f+n(i)<A)
x0 = x(i,:);
f = f +n(i);
A = f + n(i);
xbest = x0;
break;
end
end
if(key==0) %新解变动方式不受Tabu表限制
f = f + n(i);
x0 = x(i,:);
tabu = [tabu;p(i,:)];
if(f+n(i)<A) A = f + n(i); xbest = x0;end
break;
end
end
%-----------禁忌表超过tabusize更新-----------%
if(length(tabu)>tabusize)
tabu = tabu(2:end,:);
end
A_iter = [A_iter,A];
f_iter = [f_iter,f];
end
disp('最短距离:');
A
disp('最佳路径规划:');
xbest
figure(1);
plot([citys(xbest,1);citys(xbest(1),1)],[citys(xbest,2);citys(xbest(1),2)],'o-');
title('路径规划');
figure(2);
plot(A_iter);
xlabel('迭代次数');
ylabel('渴望水平');
figure(3);
plot(f_iter);
xlabel('迭代次数');
ylabel('f');
toc
- TSP(100城市)结果显示