【一文读懂卷积神经网络(四)】可能是你看过的最全的CNN(步长不为1,有填充)
本系列将由浅入深的介绍卷积神经网络的前向传播与后向传播,池化层的前向传播与后向传播,并分别介绍在不同步长与不同填充的情况下卷积层和池化层的前向传播与后向传播又有哪些不同。最后给出完整的Python实现代码。
完整目录如下:
一、CNN ⇒ \Rightarrow ⇒步长为1,无填充的卷积神经网络
二、CNN ⇒ \Rightarrow ⇒步长为1,有填充的卷积神经网络
三、CNN ⇒ \Rightarrow ⇒步长不为1,无填充的卷积神经网络
四、CNN ⇒ \Rightarrow ⇒步长不为1,有填充的卷积神经网络
CNN卷积神经网络的原理【附Python实现】
- 1. CNN的前向传播(有填充,步长strides不为1)
- 1.1 卷积层的前向传播
- 1.2 池化层的前向传播
- 2. CNN的反向传播(无填充,步长strides不为1)
- 2.1 池化层的反向传播
- 2.1.1 最大池化的反向传播
- 2.1.2 均值池化的反向传播
- 2.2 卷积层的反向传播
- 2.2.1 求dW
- 2.3.2 求dA
- 2.3.3 求db
- 3. 全部代码
上一篇文章已经介绍了 无填充,步长不为1的卷积神经网络,本文将继续由浅入深的介绍有填充,步长不为1的卷积神经网络的前向传播与后向传播,有填充的池化层的前向传播与后向传播。
1. CNN的前向传播(有填充,步长strides不为1)
1.1 卷积层的前向传播
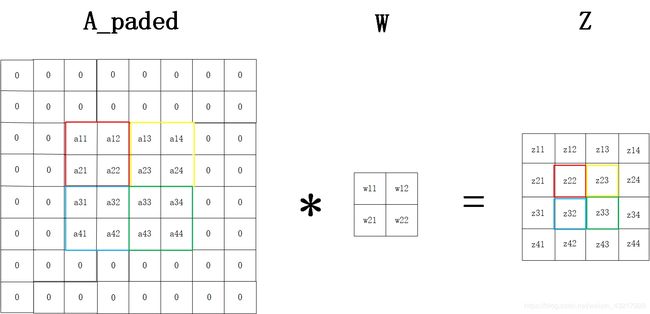
给定输入4x4的矩阵A,2x2的卷积核W,要使A和W做步长为2的卷积后的输出矩阵Z的大小和A一样,我们需要对A做填充,由 n H = ⌊ n H p r e v − f + 2 × p a d s t r i d e s ⌋ + 1 n_{H}=\lfloor{\frac{n_{Hprev}-f+2\times pad}{strides}}\rfloor+1 nH=⌊stridesnHprev−f+2×pad⌋+1我们可得需要填充的大小为 p a d = s t r i d e s × ( n H − 1 ) − n H p r e v + f 2 = 2 × ( 4 − 1 ) − 4 + 2 2 = 2 pad=\frac{strides\times(n_{H}-1)-n_{Hprev}+f}{2}=\frac{2\times (4-1)-4+2}{2}=2 pad=2strides×(nH−1)−nHprev+f=22×(4−1)−4+2=2,A被填充为8x8的A_paded,示意图如下。
1.2 池化层的前向传播
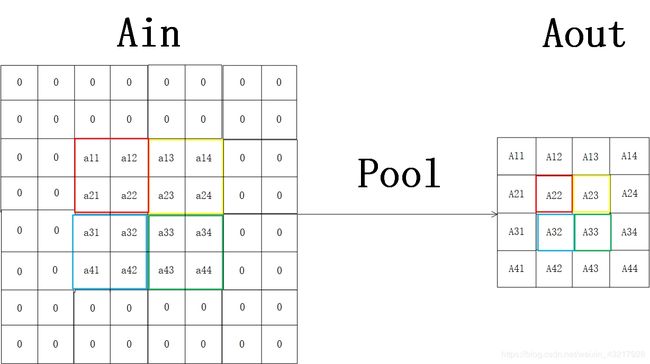
给定输入4x4的矩阵Ain,2x2的池化核,对Ain做步长为2的池化,要使池化前后大小不变,需要对Ain做填充,填充大小与卷积时计算相同, p a d = s t r i d e s × ( n H − 1 ) − n H p r e v + f 2 = 2 × ( 4 − 1 ) − 4 + 2 2 = 2 pad=\frac{strides\times(n_{H}-1)-n_{Hprev}+f}{2}=\frac{2\times (4-1)-4+2}{2}=2 pad=2strides×(nH−1)−nHprev+f=22×(4−1)−4+2=2,池化示意图如下。
2. CNN的反向传播(无填充,步长strides不为1)
对于上述前向传播,我们将损失定义为loss,我们的目标是去minimize loss,记loss对某个参数x的偏导数为dx,先来看看池化层的反向传播。
2.1 池化层的反向传播
loss对池化层输入 A 1 A^{1} A1的偏导数为 d A i n 1 dA^{1}_{in} dAin1,池化层的反向传播的数学表达式可写为 d A i n 1 = d A o u t 1 × d A o u t 1 d A i n 1 dA^{1}_{in}=dA^{1}_{out}\times \frac{dA^{1}_{out}}{dA^{1}_{in}} dAin1=dAout1×dAin1dAout1,其中最关键的一步是搞清楚 d A o u t 1 d A i n 1 \frac{dA^{1}_{out}}{dA^{1}_{in}} dAin1dAout1怎么求。我们由之前的介绍可知,池化层分为最大池化和均值池化,我们来分别探讨这两种情况。
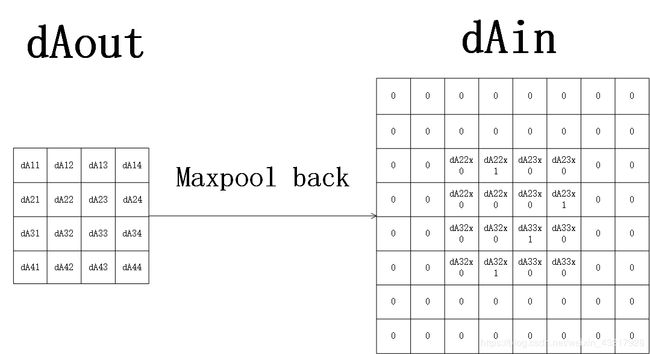
2.1.1 最大池化的反向传播
假定给定2x2的池化核,设定步长为2,部分池化核区域内的最大值由彩色方框框出。则对填充后的Ain进行最大池化后的示意图如下。
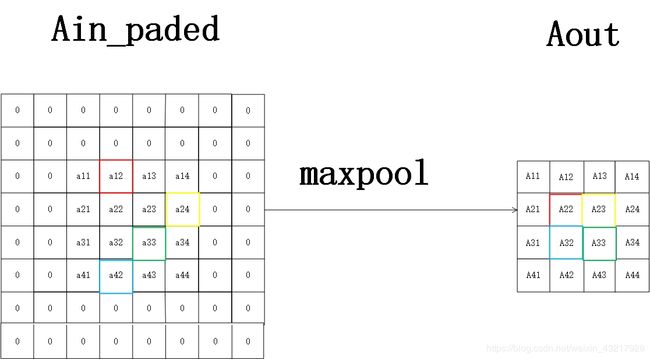
则我们可知
A 11 = 0 A11=0 A11=0, A 12 = 0 A12=0 A12=0, A 13 = 0 A13=0 A13=0, A 14 = 0 A14=0 A14=0
A 12 = 0 A12=0 A12=0
A 22 = 0 × a 11 + 1 × a 12 + 0 × a 21 + 0 × a 22 A22=0\times a11+1\times a12+0\times a21+0\times a22 A22=0×a11+1×a12+0×a21+0×a22
A 23 = 0 × a 13 + 0 × a 14 + 0 × a 23 + 1 × a 24 A23=0\times a13+0\times a14+0\times a23+1\times a24 A23=0×a13+0×a14+0×a23+1×a24
A 24 = 0 A24=0 A24=0
A 31 = 0 A31=0 A31=0
A 32 = 0 × a 31 + 0 × a 32 + 0 × a 41 + 1 × a 42 A32=0\times a31+0\times a32+0\times a41+1\times a42 A32=0×a31+0×a32+0×a41+1×a42
A 33 = 1 × a 33 + 0 × a 34 + 0 × a 43 + 0 × a 44 A33=1\times a33+0\times a34+0\times a43+0\times a44 A33=1×a33+0×a34+0×a43+0×a44
A 34 = 0 A34=0 A34=0
A 41 = 0 A41=0 A41=0, A 42 = 0 A42=0 A42=0, A 43 = 0 A43=0 A43=0, A 44 = 0 A44=0 A44=0
所以可得部分反向传播为(其他的都为0)
d A 22 d a 11 = 0 , d A 22 d a 12 = 1 , d A 22 d a 21 = 0 , d A 22 d a 22 = 0 \frac{dA22}{da11}=0,\frac{dA22}{da12}=1,\frac{dA22}{da21}=0,\frac{dA22}{da22}=0 da11dA22=0,da12dA22=1,da21dA22=0,da22dA22=0
d A 23 d a 13 = 0 , d A 23 d a 14 = 0 , d A 23 d a 23 = 0 , d A 23 d a 24 = 1 \frac{dA23}{da13}=0,\frac{dA23}{da14}=0,\frac{dA23}{da23}=0,\frac{dA23}{da24}=1 da13dA23=0,da14dA23=0,da23dA23=0,da24dA23=1
d A 32 d a 31 = 0 , d A 32 d a 32 = 0 , d A 32 d a 41 = 0 , d A 32 d a 42 = 1 \frac{dA32}{da31}=0,\frac{dA32}{da32}=0,\frac{dA32}{da41}=0,\frac{dA32}{da42}=1 da31dA32=0,da32dA32=0,da41dA32=0,da42dA32=1
d A 33 d a 33 = 1 , d A 33 d a 34 = 1 , d A 33 d a 43 = 0 , d A 33 d a 44 = 0 \frac{dA33}{da33}=1,\frac{dA33}{da34}=1,\frac{dA33}{da43}=0,\frac{dA33}{da44}=0 da33dA33=1,da34dA33=1,da43dA33=0,da44dA33=0
即 d A i n _ p a d e d 1 = u p s a m p l e ( d A o u t 1 ) dA^{1}_{in\_paded}=upsample(dA^{1}_{out}) dAin_paded1=upsample(dAout1),其中upsample是指将 d A o u t 1 dA^{1}_{out} dAout1上采样至和 d A i n _ p a d e d 1 dA^{1}_{in\_paded} dAin_paded1一样的shape,而 d A o u t 1 dA^{1}_{out} dAout1里的每个值所在位置由 d A i n _ p a d e d 1 dA^{1}_{in\_paded} dAin_paded1里每个池化核区域内的最大值决定,同时池化核区域移动的步长由和正向传播时的步长一样。
可知,我们需要在正向传播时记住各个池化核大小区域内最大值的位置和步长,即可求得 d A i n _ p a d e d 1 dA^{1}_{in\_paded} dAin_paded1,但我们还需要将 d A i n _ p a d e d 1 dA^{1}_{in\_paded} dAin_paded1恢复为 A i n 1 A^{1}_{in} Ain1填充之前的大小,所以需要进行delete操作,即删除填充的行和列。
以下给出这一方法的python实现(为了简便易懂,假设只有一个输入样本且为单通道,但实际情况往往不是这样。)
def max_pool_backward(self,dAout,Ain_paded,filterSize,strides):
#params说明
#params dAout为传入的dAout
#params Ain_paded为我们记录的正向传播时当前池化层经填充后的输入,我们将用来它来计算每个池化核区域内的最大值
#params filterSize为池化核的大小
#params strides为池化层的步长
#return dAin_paded
dAin_paded=np.zeros_like(Ain_paded) #初始化dAin_paded为shape和Ain_paded相同,值为0的矩阵
n_H,n_W=dAout.shape #n_H,n_W分别是dAout的高和宽
for h in range(n_H): #遍历行
for w in range(n_W): #遍历列
h_start=h*strides #当前池化区域行的开头
h_end=h_start+filterSize #当前池化区域行的结尾
w_start=w*strides #当前池化区域列的开头
w_end=w_start+filterSize #当前池化区域列的结尾
mask=(Ain_paded[h_start:h_end,w_start:w_end]==np.max(Ain_paded[h_start:h_end,w_start:w_end]))
#找到当前池化区域内最大值的位置,在mask内,最大值的位置将会等于True(1),其他位置都等于False(0)
dAin_paded[h_start:h_end,w_start:w_end]=mask*dAout[h,w] #实现对dAout的upsample
return dAin_paded
def delete_pad(self,dA,pad_size):
///这是一种复杂的写法,意在让大家熟悉下numpy的这个方法,在后面提到的优化代码里有简单方法。
#params说明
#params dA为传入的需要去掉填充的参数
#params pad_size为正向传播时填充的大小,是一个tuple,分别保存了行和列方向上填充的大小
#return dA
pad_h_size,pad_w_size=pad_size #填充的大小
m,n_H_prev,n_W_prev,n_C=dA.shape #填充后的大小
#计算出填充前的大小
n_H=n_H_prev-2*pad_h_size
n_W=n_W_prev-2*pad_w_size
#需要删除的行和列的list
delete_h_list=[h for h in range(pad_h_size)]
delete_w_list=[w for w in range(pad_w_size)]
for i in range(pad_h_size):
delete_h_list.append((i+n_H+pad_h_size))
for j in range(pad_w_size):
delete_w_list.append((j+n_W+pad_w_size))
dA=np.delete(dA,delete_h_list,axis=1)
dA=np.delete(dA,delete_w_list,axis=2)
return dA
2.1.2 均值池化的反向传播
假定给定2x2的池化核,设定步长为2,以下是有填充的均值池化正向传播的示意图。
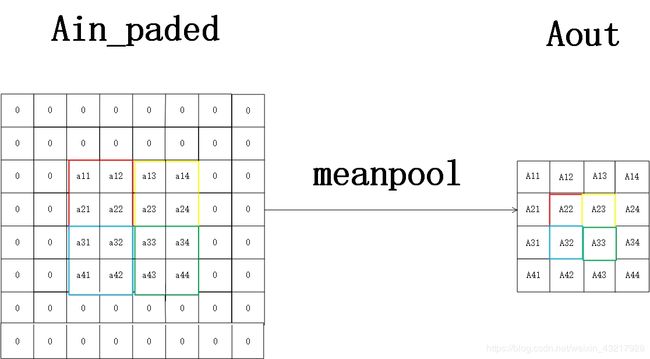
我们可知
A 11 = 0 A11=0 A11=0, A 12 = 0 A12=0 A12=0, A 13 = 0 A13=0 A13=0, A 14 = 0 A14=0 A14=0
A 21 = 0 A21=0 A21=0
A 22 = ( a 11 + a 12 + a 21 + a 22 ) ÷ 4 A22=(a11+a12+a21+a22)\div4 A22=(a11+a12+a21+a22)÷4
A 23 = ( a 13 + a 14 + a 23 + a 24 ) ÷ 4 A23=(a13+a14+a23+a24)\div4 A23=(a13+a14+a23+a24)÷4
A 24 = 0 A24=0 A24=0
A 31 = 0 A31=0 A31=0
A 32 = ( a 31 + a 32 + a 41 + a 42 ) ÷ 4 A32=(a31+a32+a41+a42)\div4 A32=(a31+a32+a41+a42)÷4
A 33 = ( a 33 + a 34 + a 43 + a 44 ) ÷ 4 A33=(a33+a34+a43+a44)\div4 A33=(a33+a34+a43+a44)÷4
A 34 = 0 A34=0 A34=0
A 41 = 0 A41=0 A41=0, A 42 = 0 A42=0 A42=0, A 43 = 0 A43=0 A43=0, A 44 = 0 A44=0 A44=0
可得部分反向传播为(其余的都为0)
d A 22 d a 11 = d A 22 d a 12 = d A 22 d a 21 = d A 22 d a 22 = 1 4 \frac{dA22}{da11}=\frac{dA22}{da12}=\frac{dA22}{da21}=\frac{dA22}{da22}=\frac{1}{4} da11dA22=da12dA22=da21dA22=da22dA22=41
d A 23 d a 13 = d A 23 d a 14 = d A 23 d a 23 = d A 23 d a 24 = 1 4 \frac{dA23}{da13}=\frac{dA23}{da14}=\frac{dA23}{da23}=\frac{dA23}{da24}=\frac{1}{4} da13dA23=da14dA23=da23dA23=da24dA23=41
d A 32 d a 31 = d A 32 d a 32 = d A 32 d a 41 = d A 32 d a 42 = 1 4 \frac{dA32}{da31}=\frac{dA32}{da32}=\frac{dA32}{da41}=\frac{dA32}{da42}=\frac{1}{4} da31dA32=da32dA32=da41dA32=da42dA32=41
d A 33 d a 33 = d A 33 d a 34 = d A 33 d a 43 = d A 33 d a 44 = 1 4 \frac{dA33}{da33}=\frac{dA33}{da34}=\frac{dA33}{da43}=\frac{dA33}{da44}=\frac{1}{4} da33dA33=da34dA33=da43dA33=da44dA33=41
因此我们可得步长为2,有填充的均值池化的反向传播为
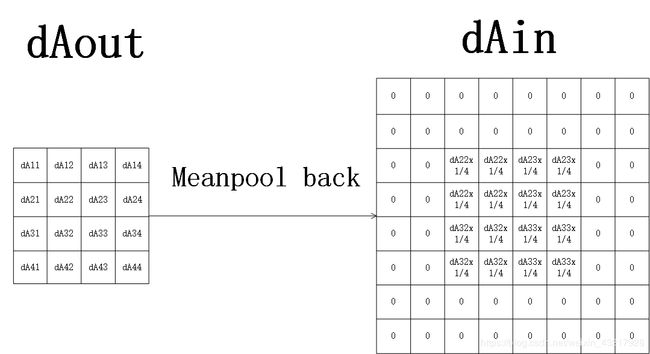
即 d A i n _ p a d e d 1 = u p s a m p l e ( d A o u t 1 ) dA^{1}_{in\_paded}=upsample(dA^{1}_{out}) dAin_paded1=upsample(dAout1),这里的upsample和最大池化里的略有不同,是将 d A o u t 1 dA^{1}_{out} dAout1上采样至和 A i n _ p a d e d 1 A^{1}_{in\_paded} Ain_paded1一样的shape,每个位置上的值为对应的 d A o u t 1 dA^{1}_{out} dAout1的值除上池化核大小的平方。
可知,我们需要在正向传播时记住池化核的大小和步长,即可求得 d A i n _ p a d e d 1 dA^{1}_{in\_paded} dAin_paded1,但我们还需要将 d A i n _ p a d e d 1 dA^{1}_{in\_paded} dAin_paded1恢复为 A i n 1 A^{1}_{in} Ain1填充之前的大小,所以需要进行delete操作,即删除填充的行和列。
以下给出这一方法的python实现(为了简便易懂,假设只有一个输入样本且为单通道,但实际情况往往不是这样。)
def average_pool_backward(self,dAout,Ain_paded,filterSize,strides):
#params说明
#params dAout为传入的dAout
#params Ain_paded为我们记录的正向传播时当前层填充后池化的输入,我们将用来它来计算每个池化核区域内的平均值
#params filterSize为池化核的大小
#params strides为池化层的步长
#return dAin_paded
dAin_paded = np.zeros_like(Ain_paded) #初始化dAin_paded 为shape和Ain_paded相同,值为0的矩阵
n_H, n_W = dAout.shape #n_H,n_W分别是dAout的高和宽
for h in range(n_H): #遍历行
for w in range(n_W): #遍历列
h_start = h * strides #当前池化区域行的开头
h_end = h_start + filterSize #当前池化区域行的结尾
w_start = w * strides #当前池化区域列的开头
w_end = w_start + filterSize #当前池化区域列的结尾
dAin_paded [h_start:h_end,w_start:w_end]+=np.ones((filterSize,filterSize))*(dAout[h,w]/(filterSize**2))
#1/(filterSize**2)为池化区域内对每个值的导数,再将它上采样至池化核的大小
return dAin_paded
def delete_pad(self,dA,pad_size):
///这是一种复杂的写法,意在让大家熟悉下numpy的这个方法,在后面提到的优化代码里有简单方法。
#params说明
#params dA为传入的需要去掉填充的参数
#params pad_size为正向传播时填充的大小,是一个tuple,分别保存了行和列方向上填充的大小
#return dA
pad_h_size,pad_w_size=pad_size #填充的大小
m,n_H_prev,n_W_prev,n_C=dA.shape #填充后的大小
#计算出填充前的大小
n_H=n_H_prev-2*pad_h_size
n_W=n_W_prev-2*pad_w_size
#需要删除的行和列的list
delete_h_list=[h for h in range(pad_h_size)]
delete_w_list=[w for w in range(pad_w_size)]
for i in range(pad_h_size):
delete_h_list.append((i+n_H+pad_h_size))
for j in range(pad_w_size):
delete_w_list.append((j+n_W+pad_w_size))
dA=np.delete(dA,delete_h_list,axis=1)
dA=np.delete(dA,delete_w_list,axis=2)
return dA
2.2 卷积层的反向传播
关于卷积层的反向传播,我们需要求三个值,一个是dW,第二个是dA(即上一池化层的输出,本层的输入),第三个是db,当求得dW,db后,就可以选用梯度下降法,Adam等优化算法来更新参数,直至满足停止条件最终得到模型。
首先来看看如何求dW。
2.2.1 求dW
求dW的反向传播的数学表达式可写为 d W 0 = d Z 1 × d Z 1 d W 0 dW^{0}=dZ^{1}\times \frac{dZ^{1}}{dW^{0}} dW0=dZ1×dW0dZ1,其中 d Z 1 dZ^{1} dZ1已由上面池化层的反向传播和relu的反向传播求得,关键就是求解 d Z 1 d W 0 \frac{dZ^{1}}{dW^{0}} dW0dZ1,先回顾一下卷积层的正向传播,给定4x4的输入矩阵A,2x2的卷积核W,将A填充为8x8的矩阵A_paded,然后让A_paded与W做步长为2的卷积,可以得到4x4的输出矩阵Z,示意图如下。注意这里的A为上一层池化层的输出!!(如果为第一层的话,则为输入样本数据)
z 11 = 0 , z 12 = 0 , z 13 = 0 , z 14 = 0 z11=0,z12=0,z13=0,z14=0 z11=0,z12=0,z13=0,z14=0
z 21 = 0 z21=0 z21=0
z 22 = a 11 × w 11 + a 12 × w 12 + a 21 × w 21 + a 22 × w 22 z22=a11\times w11+a12\times w12+a21\times w21+a22\times w22 z22=a11×w11+a12×w12+a21×w21+a22×w22
z 23 = a 13 × w 11 + a 14 × w 12 + a 23 × w 21 + a 24 × w 22 z23=a13\times w11+a14\times w12+a23\times w21+a24\times w22 z23=a13×w11+a14×w12+a23×w21+a24×w22
z 24 = 0 z24=0 z24=0
z 31 = 0 z31=0 z31=0
z 32 = a 31 × w 11 + a 32 × w 12 + a 41 × w 21 + a 42 × w 22 z32=a31\times w11+a32\times w12+a41\times w21+a42\times w22 z32=a31×w11+a32×w12+a41×w21+a42×w22
z 33 = a 33 × w 11 + a 34 × w 12 + a 43 × w 21 + a 44 × w 22 z33=a33\times w11+a34\times w12+a43\times w21+a44\times w22 z33=a33×w11+a34×w12+a43×w21+a44×w22
z 34 = 0 z34=0 z34=0
z 41 = 0 , z 42 = 0 , z 43 = 0 , z 44 = 0 z41=0,z42=0,z43=0,z44=0 z41=0,z42=0,z43=0,z44=0
于是
d w 11 = d z 22 × a 11 + d z 23 × a 13 + d z 32 × a 31 + d z 33 × a 33 dw11=dz22\times a11+dz23\times a13+dz32\times a31+dz33\times a33 dw11=dz22×a11+dz23×a13+dz32×a31+dz33×a33
d w 12 = d z 22 × a 12 + d z 23 × a 14 + d z 32 × a 32 + d z 33 × a 34 dw12=dz22\times a12+dz23\times a14+dz32\times a32+dz33\times a34 dw12=dz22×a12+dz23×a14+dz32×a32+dz33×a34
d w 21 = d z 22 × a 21 + d z 23 × a 23 + d z 32 × a 41 + d z 33 × a 43 dw21=dz22\times a21+dz23\times a23+dz32\times a41+dz33\times a43 dw21=dz22×a21+dz23×a23+dz32×a41+dz33×a43
d w 22 = d z 22 × a 22 + d z 23 × a 24 + d z 32 × a 42 + d z 33 × a 44 dw22=dz22\times a22+dz23\times a24+dz32\times a42+dz33\times a44 dw22=dz22×a22+dz23×a24+dz32×a42+dz33×a44
将上述公式总结一下,给出一张示意图帮助理解。
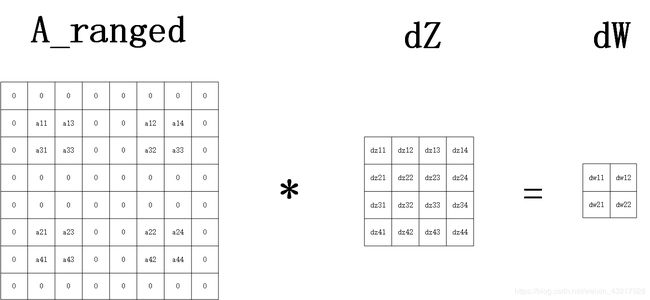
**对于A_ranged,我们可以由两种理解。
1.将A的第2列与第3列交换,第3列与第5列交换,第4列与第6列交换,在把A的第2行与第3行交换,第3行与第5行交换,第4行与第6行交换。更普遍的,将A的第j列与第j-1+strides列交换,之后把A的第j列与第j+strides列交换,在把A的第j行与第j-1+strides行交换,之后把A的第j行与第j+strides行交换,之后依此类推。
2.对于每个卷积区域的元素,我们可以这样得到,以第一个卷积区域为例,应该是对正常的A取(1,1),(1,1+strides),(1,1+strides+strides),(1,1+strides+strides+strides),(第一行)
(1+strides,1),(1+strides,1+strides),(1+strides,1+strides+strides),(1+strides,1+strides+strides+strides),(第二行)
(1+strides+strides,1),(1+strides+strides,1+strides),(1+strides+strides,1+strides+strides),(1+strides+strides,1+strides+strides+strides),(第三行)
(1+strides+strides+strides,1),(1+strides+strides+strides,1+strides),(1+strides+strides+strides,1+strides+strides),(1+strides+strides+strides,1+strides+strides+strides),(第四行)
这十六个元素得到,取出来正好也等于0,0,0,0,0,a11,a13,0,0,0,a31,a33,0,0,0,0,0之后的卷积区域依此类推。**
由此可见,我们在正向传播时应把上一层池化后的输出在进行卷积时填充后的A_paded和步长记录下来,在反向传播求dW时,只需将记录的正向传播时的A_paded作为输入,对A按上述两种方法任一处理得到A_ranged,之后与dZ做步长为dZ的大小相同,有填充的卷积,即可完成计算。
以下给出这一方法的python实现(为了简便易懂,假设只有一个输入样本且为单通道,但实际情况往往不是这样。)
def conv_backward(self,dZ,Aout_paded,filterSize,strides): #卷积层的后向传播
#params说明
#params dZ传入的对当前卷积层输出的导数
#params Aout_paded当前卷积层经填充后正向传播时的输入,我们用它来与dZ做卷积
#params filterSize卷积核的大小
#params strides卷积的步长
#return dW
dW=np.zeros((filterSize,filterSize)) #初始化dW
n_H,n_W=dZ.shape #dZ的高宽
for m in range(filterSize): #遍历行
for n in range(filterSize): #遍历列
for i in range(n_H):
for j in range(n_W):
h= i * strides + m
w= j * strides + n
dW[m,n]+=Aout_paded[h,w]*dZ[i,j]
return dW
2.3.2 求dA
借助上述卷积层的正向传播,我们可以得到
d a 11 = d z 22 × w 11 , d a 12 = d z 22 × w 12 , d a 21 = d z 22 × w 21 , d a 22 = d z 22 × w 22 da11=dz22\times w11,da12=dz22\times w12,da21=dz22\times w21,da22=dz22\times w22 da11=dz22×w11,da12=dz22×w12,da21=dz22×w21,da22=dz22×w22
d a 13 = d z 23 × w 11 , d a 14 = d z 23 × w 12 , d a 23 = d z 23 × w 21 , d a 24 = d z 23 × w 22 da13=dz23\times w11,da14=dz23\times w12,da23=dz23\times w21,da24=dz23\times w22 da13=dz23×w11,da14=dz23×w12,da23=dz23×w21,da24=dz23×w22
d a 31 = d z 32 × w 11 , d a 32 = d z 32 × w 12 , d a 41 = d z 32 × w 21 , d a 42 = d z 32 × w 22 da31=dz32\times w11,da32=dz32\times w12,da41=dz32\times w21,da42=dz32\times w22 da31=dz32×w11,da32=dz32×w12,da41=dz32×w21,da42=dz32×w22
d a 33 = d z 33 × w 11 , d a 34 = d z 33 × w 12 , d a 43 = d z 33 × w 21 , d a 44 = d z 33 × w 22 da33=dz33\times w11,da34=dz33\times w12,da43=dz33\times w21,da44=dz33\times w22 da33=dz33×w11,da34=dz33×w12,da43=dz33×w21,da44=dz33×w22
我们整理一下,可以得到下图
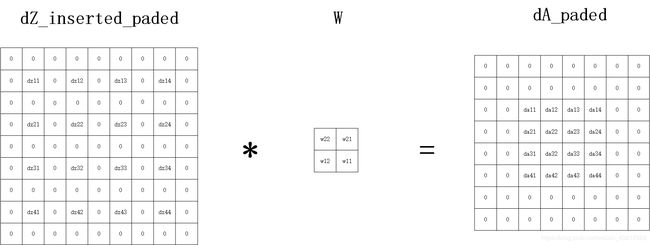
即 d A = p a d ( i n s e r t ( d Z ) ) ∗ r o t 180 ( W ) dA=pad(insert(dZ))\ast rot180(W) dA=pad(insert(dZ))∗rot180(W)
我们可以看到对于求反向传播时的dA,我们首先需要对dZ做insert操作,即每两行(列)之间填充(strides-1)行和填充(strides-1)列,然后再对dZ做pad操作(填充),填充的大小为 p a d = ( n H − 1 ) − n H p r e v + f 2 = ( 8 − 1 ) − 7 + 2 2 = 1 pad=\frac{(n_{H}-1)-n_{Hprev}+f}{2}=\frac{(8-1)-7+2}{2}=1 pad=2(nH−1)−nHprev+f=2(8−1)−7+2=1,然后与沿顺时针旋转180度的卷积核W做步长为1!!!步长为1!!!步长为1!!!的卷积操作(无论正向传播时strides是多少),得到的是填充后的dA,反向传播时,我们只需要更新填充前的大小,因此还需要deletePad(dA)。
以下给出这一方法的python实现(为了简便易懂,假设只有一个输入样本且为单通道,但实际情况往往不是这样。)
def zero_insert(self,dZ,insert_size):
H,W=dZ.shape
dZout=dZ
insert_values_h=np.zeros((insert_size,W))
for h in range(H-1):
dZout=np.insert(dZout,h*(1+insert_size)+1,values=insert_values_h,axis=0)
insert_values_w = np.zeros((insert_size,dZ.shape[1]))
for w in range(W-1):
dZout=np.insert(dZout,w*(1+insert_size) + 1,values=insert_values_w,axis=1)
return dZout
def conv_backward(self,dZ,Aout_paded,convFilter,filterSize,strides): #卷积层的后向传播
#params说明
#params dZ传入的对当前卷积层输出的导数
#params Aout_paded正向传播时该层填充后的的输入
#params convFilter当前卷积层正向传播时的卷积核
#params filterSize卷积核的大小
#params strides卷积的步长
#return dA
convFilter=convFilter[:,:,::-1,::-1]
n_H,n_W=Aout_paded.shape
dA_paded=np.zeros_like(Aout_paded) #初始化dA和Aout一样的shape,数值为0
dZ_inserted = self.zero_insert(dZ, strides - 1) #对dZ做insert操作
insertH,insertW=dZ_inserted.shape
pad_size_h=(n_H-1-insertH+filterSize)/2 #填充的大小
pad_size_w=(n_W-1-insertW+filterSize)/2 #填充的大小
dZ_paded=np.pad(dZ,(pad_size_h,pad_size_w),'constant') #对dZ做填充,填充的值为0
for h in range(n_H):
for w in range(n_W):
dA_paded[h,w]=np.sum(np.multiply(dZ_paded[h:h+filterSize,w:w+filterSize],convFilter))
return dA_paded
def delete_pad(self,dA,pad_size):
///这是一种复杂的写法,意在让大家熟悉下numpy的这个方法,在后面提到的优化代码里有简单方法。
#params说明
#params dA为传入的需要去掉填充的参数
#params pad_size为正向传播时填充的大小,是一个tuple,分别保存了行和列方向上填充的大小
#return dA
pad_h_size,pad_w_size=pad_size #填充的大小
m,n_H_prev,n_W_prev,n_C=dA.shape #填充后的大小
#计算出填充前的大小
n_H=n_H_prev-2*pad_h_size
n_W=n_W_prev-2*pad_w_size
#需要删除的行和列的list
delete_h_list=[h for h in range(pad_h_size)]
delete_w_list=[w for w in range(pad_w_size)]
for i in range(pad_h_size):
delete_h_list.append((i+n_H+pad_h_size))
for j in range(pad_w_size):
delete_w_list.append((j+n_W+pad_w_size))
dA=np.delete(dA,delete_h_list,axis=1)
dA=np.delete(dA,delete_w_list,axis=2)
return dA
2.3.3 求db
对于求db比较简单,db=dZ,只是需要对dZ在某个维度上做累加运算即可得到。
以下给出求db的python实现(为了简便易懂,假设只有一个输入样本且为单通道,但实际情况往往不是这样。)
def conv_backward(self,dZ): #卷积层的后向传播
db=np.sum(dZ)
return db
以上就是有填充,步长不为1的卷积神经网络的原理,整个卷积神经网络的系列到此就结束了。希望读者看完之后有所收获,共同进步。
所有源代码在文末
码字作图实属不易,前前后后断断续续用了不少时间,希望大家看后能有所收获,觉得可以的给点赞赏,让我有走下去的动力。谢谢大家!
大家看完python实现的方法是否会发现效率过于低下,因为其中有大量的for循环,博主本人花费了一些时间优化了代码,使速度有了很大的提升(最快的由6个for循环降为2个for循环),有兴趣的小伙伴可以在打赏我后评论或私聊我,我将代码发给你。请见谅。
![]()
![]()
3. 全部代码
Github见所有Python代码