#数据结构#第五章：树、森林、哈夫曼树

判断题

1-1.对于一个有N个结点、K条边的森林，不能确定它共有几棵树。

F， NodeNum - 1 = EdgeNum；设森林里有TreeNum颗数， 则TotalNodeNum - TreeNum = TotalEdgeNum；即 在此题中N - TreeNum = K;

1-2.对N（≥2）个权值均不相同的字符构造哈夫曼树，则树中任一非叶结点的权值一定不小于下一层任一结点的权值.

T

单选题

2-1.具有1102个结点的完全二叉树一定有__个叶子结点。

A.79
B.551
C.1063
D.不确定

B
边数n=节点数-1，即n=1101；
n=2n2+n1;
完全二叉树度为1的节点只能有0个或1个
所以n1=0或者1
用n=2n2+n1;算一下，n2=550；
n0=n2+1=551

2-2.若森林F有15条边、25个结点，则F包含树的个数是：

A.8
B.9
C.10
D.11

C,25-15=10

2-3.将森林转换为对应的二叉树，若在二叉树中，结点u是结点v的父结点的父结点，则在原来的森林中，u和v可能具有的关系是：
1.父子关系； 2. 兄弟关系； 3. u的父结点与v的父结点是兄弟关系

A.只有2
B.1和2
C.1和3
D.1、2和3

B

2-4.对于一个有N个结点、K条边的森林，共有几棵树？

A.N−K
B.N−K+1
C.N−K−1
D.不能确定

A

2-5.设森林F中有三棵树，第一、第二、第三棵树的结点个数分别为M_​1,M₂,M₃。则与森林F对应的二叉树根结点的右子树上的结点个数是：

A.M₁
B.M₁+M₂
C.M₂+M₃
D.M₃

C
​​

2-6.由若干个二叉树组成的森林F中，叶结点总个数为N，度为2的结点总个数为M，则该集合中二叉树的个数为：

A.M−N
B.N−M
C.N−M−1
D.无法确定

B

2-7.已知一棵完全二叉树的第6层（设根为第1层）有8个叶结点，则该完全二叉树的结点个数最多是：

A.39
B.52
C.111
D.119

C

2-8.在一个用数组表示的完全二叉树中，如果根结点下标为1，那么下标为17和19这两个结点的最近公共祖先结点在哪里（数组下标）？ （注：两个结点的“公共祖先结点”是指同时都是这两个结点祖先的结点）

A.8
B.4
C.2
D.1

B

2-9.具有65个结点的完全二叉树其深度为（根的深度为1）：

A.8
B.7
C.6
D.5

B

2-10.对N（N≥2）个权值均不相同的字符构造哈夫曼树。下列关于该哈夫曼树的叙述中，错误的是：

A.树中一定没有度为1的结点
B.树中两个权值最小的结点一定是兄弟结点
C.树中任一非叶结点的权值一定不小于下一层任一结点的权值
D.该树一定是一棵完全二叉树

D

2-11.设一段文本中包含字符{a, b, c, d, e}，其出现频率相应为{3, 2, 5, 1, 1}。则经过哈夫曼编码后，文本所占字节数为：

A.40
B.36
C.25
D.12

C

2-12.设一段文本中包含4个对象{a,b,c,d}，其出现次数相应为{4,2,5,1}，则该段文本的哈夫曼编码比采用等长方式的编码节省了多少位数？

A.0
B.2
C.4
D.5

B

2-13.由分别带权为9、2、5、7的四个叶子结点构成一棵哈夫曼树，该树的带权路径长度为：

A.23
B.37
C.44
D.46

C

2-14.已知字符集{ a, b, c, d, e, f, g, h }。若各字符的哈夫曼编码依次是 0100, 10, 0000, 0101, 001, 011, 11, 0001，则编码序列 0100011001001011110101 的译码结果是：

A.acgabfh
B.adbagbb
C.afbeagd
D.afeefgd

D

2-15.若以｛4，5，6，3，8｝作为叶子节点的权值构造哈夫曼树，则带权路径长度是（）。

A.28
B.68
C.55
D.59

D

2-16.下列叙述错误的是（）。

A.一棵哈夫曼树的带权路径长度等于其中所有分支结点的权值之和
B.当一棵具有n 个叶子结点的二叉树的WPL 值为最小时，称其树为哈夫曼树，其二叉树的形状是唯一的
C.哈夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近
D.哈夫曼树的结点个数不能是偶数

B

2-17.哈夫曼树是n个带权叶子结点构成的所有二叉树中（）最小的二叉树。

A.权值
B.高度
C.带权路径长度
D.度

C

2-18.(neuDS)在哈夫曼树中，任何一个结点它的度都是（ ）

A.0或1
B.1或2
C.0或2
D.0或1或2

C

程序填空题

5-1.下列代码的功能是计算给定二叉树T的宽度。二叉树的宽度是指各层结点数的最大值。函数Queue_rear和Queue_front分别返回当前队列Q中队尾和队首元素的位置。

typedef struct TreeNode *BinTree;
struct TreeNode
{
   int Key;
   BinTree  Left;
   BinTree  Right;
};

int Width( BinTree T )
{
   BinTree  p;
   Queue Q;
   int Last, temp_width, max_width;

   temp_width = max_width = 0;
   Q = CreateQueue(MaxElements);
   Last = Queue_rear(Q);
   if ( T == NULL) return 0;
   else {
      Enqueue(T, Q);
      while (!IsEmpty(Q)) {
         p = Front_Dequeue(Q); 

temp_width++;

         if ( p->Left != NULL )  Enqueue(p->Left, Q);

if(p -> Right != NULL)

         if ( Queue_front(Q) > Last ) {
            Last = Queue_rear(Q);
            if ( temp_width > max_width ) max_width = temp_width;

temp_width = 0;

 } /* end-if */
      } /* end-while */
      return  max_width;
   } /* end-else */
} 

编程题

7-1 树的同构

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

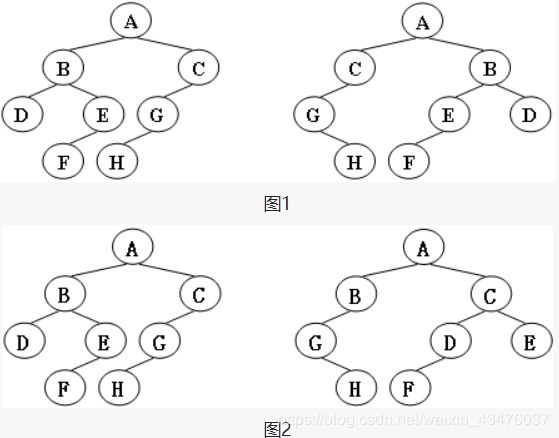
现给定两棵树，请你判断它们是否是同构的。

输入格式：

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式：

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1(对应图1)

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例

Yes

输入样例2(对应图2)

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例

No

参考代码

#include

using namespace std;

typedef struct Node
{
    char ch;
    char left;
    char right;
};

Node tree[12][2];

int n1,n2;

void CreatTree(int id)
{
    int n, i;
    scanf("%d", &n);
    if(id == 0)
        n1 = n;
    else
        n2 = n;
    char a, b, c, d, e, f;
    getchar();
    for(i = 0; i < n; ++i)
    {
        scanf("%c%c%c%c%c%c",&a,&b,&c,&d,&e,&f);
        tree[i][id].ch = a;
        if(e == '-'&& f != '-')
            swap(e, f);
        tree[i][id].left = c;
        tree[i][id].right = e;
    }
}
bool Judge()
{
    int ok = 1;
    int i, j;
    if(n1 != n2)
        return false;
    for(i = 0; i < n1; i++)
    {
        char l2, r2;
        char c1 = tree[i][0].ch, l1 = tree[i][0].left, r1 = tree[i][0].right;
        for(j = 0; j < n2; j++)
        {
            if(c1 == tree[j][1].ch)
            {
                l2 = tree[j][1].left;
                r2 = tree[j][1].right;
                break;
            }
        }
        if(j == n2)
        {
            ok = 0;
            break;
        }
        if(r1 == '-' && r2 == '-')
        {
            if(l1 == '-' && l2 == '-')
                continue;
            else if(tree[l1 - '0'][0].ch == tree[l2 - '0'][1].ch)
                continue;
            else
            {
                ok = 0;
                break;
            }
        }
        else if(((tree[l1 - '0'][0].ch == tree[l2 - '0'][1].ch)&&(tree[r1 - '0'][0].ch == tree[r2 - '0'][1].ch))||
                ((tree[l1 - '0'][0].ch == tree[r2 - '0'][1].ch)&&(tree[r1 - '0'][0].ch == tree[l2 - '0'][1].ch)))
                    continue ;
        else
        {
            ok = 0;
            break;
        }

    }
    if(ok)
        return true;
    else
        return false;
}
int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    CreatTree(0);
    CreatTree(1);
    if(Judge())
        printf("Yes\n");
    else
        printf("No\n");
    return 0;
}

7-2 家谱处理

人类学研究对于家族很感兴趣，于是研究人员搜集了一些家族的家谱进行研究。实验中，使用计算机处理家谱。为了实现这个目的，研究人员将家谱转换为文本文件。下面为家谱文本文件的实例：
John
  Robert
    Frank
    Andrew
  Nancy
     David

家谱文本文件中，每一行包含一个人的名字。第一行中的名字是这个家族最早的祖先。家谱仅包含最早祖先的后代，而他们的丈夫或妻子不出现在家谱中。每个人的子女比父母多缩进2个空格。以上述家谱文本文件为例，John这个家族最早的祖先，他有两个子女Robert和Nancy，Robert有两个子女Frank和Andrew，Nancy只有一个子女David。

在实验中，研究人员还收集了家庭文件，并提取了家谱中有关两个人关系的陈述语句。下面为家谱中关系的陈述语句实例：

John is the parent of Robert
Robert is a sibling of Nancy
David is a descendant of Robert

研究人员需要判断每个陈述语句是真还是假，请编写程序帮助研究人员判断。

输入格式：

输入首先给出2个正整数N（2≤N≤100）和M（≤100），其中N为家谱中名字的数量，M为家谱中陈述语句的数量，输入的每行不超过70个字符。

名字的字符串由不超过10个英文字母组成。在家谱中的第一行给出的名字前没有缩进空格。家谱中的其他名字至少缩进2个空格，即他们是家谱中最早祖先（第一行给出的名字）的后代，且如果家谱中一个名字前缩进k个空格，则下一行中名字至多缩进k+2个空格。

在一个家谱中同样的名字不会出现两次，且家谱中没有出现的名字不会出现在陈述语句中。每句陈述语句格式如下，其中X和Y为家谱中的不同名字：

X is a child of Y
X is the parent of Y
X is a sibling of Y
X is a descendant of Y
X is an ancestor of Y

输出格式：

对于测试用例中的每句陈述语句，在一行中输出True，如果陈述为真，或False，如果陈述为假。

输入样例

6 5
John
  Robert
    Frank
    Andrew
  Nancy
    David
Robert is a child of John
Robert is an ancestor of Andrew
Robert is a sibling of Nancy
Nancy is the parent of Frank
John is a descendant of Andrew

输出样例

True
True
True
False
False

参考代码

#include 

using namespace std;

int main()
{
    vector<string> name(101);     
    map<string, string> father; 
    int n, m;
    scanf("%d %d", &n, &m);
    getchar();
    while(n--)
    {
        string str;
        getline(cin, str);
        int cnt = count(str.begin(), str.end(), ' ');
        if(cnt == 0)
        {
            father[str] = "root";
            name[0] = str;
        }
        else
        {
            str = str.substr(cnt);
            father[str] = name[cnt / 2 - 1];
            name[cnt / 2] = str;
        }
    }
    while(m--)
    {
        string a, b, c, d;
        cin >> a >> b >> b >> c >> b >> d;
        switch(c[0])
        {
            case 'p':
                swap(a, d);
            case 'c':
                if(father[a] == d)
                    printf("True\n");
                else
                    printf("False\n");
                break;
            case 's':
                if(father[a] == father[d])
                    printf("True\n");
                else
                    printf("False\n");
                break;
            case 'a':
                swap(a, d);
            case 'd':
                while(father[a] != d && father[a] != "root") 
                    a = father[a];
                if(father[a] == "root")
                    printf("False\n");
                else
                    printf("True\n");
        }
    }
    return 0;
}

7-3 修理牧场

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要N块木头，每块木头长度为整数L_​i个长度单位，于是他购买了一条很长的、能锯成N块的木头，即该木头的长度是L_i的总和。

但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为20的木头锯成长度为8、7和5的三段，第一次锯木头花费20，将木头锯成12和8；第二次锯木头花费12，将长度为12的木头锯成7和5，总花费为32。如果第一次将木头锯成15和5，则第二次锯木头花费15，总花费为35（大于32）。

请编写程序帮助农夫计算将木头锯成N块的最少花费。

输入格式：

输入首先给出正整数N（≤10^​4），表示要将木头锯成N块。第二行给出N个正整数（≤50），表示每段木块的长度。

输出格式：

输出一个整数，即将木头锯成N块的最少花费。

输入样例

8
4 5 1 2 1 3 1 1

输出样例

49

参考代码

#include 

using namespace std;

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    priority_queue<int,vector<int>,greater<int> >l;//优先队列
    int n, data, i;
    cin>>n;
    for(i = 0; i < n; i++)
    {
        cin>>data;
        l.push(data);
    }
    int sum = 0;
    while(l.size() != 1)
    {
        int x = l.top();
        l.pop();
        int y = l.top();
        l.pop();
        sum += x + y;
        l.push(x + y);
    }
    printf("%d\n", sum);
    return 0;
}