PTA部分数据结构代码
大二下学期数据结构练习代码
- 重排链表
- 一元多项式的乘法与加法运算
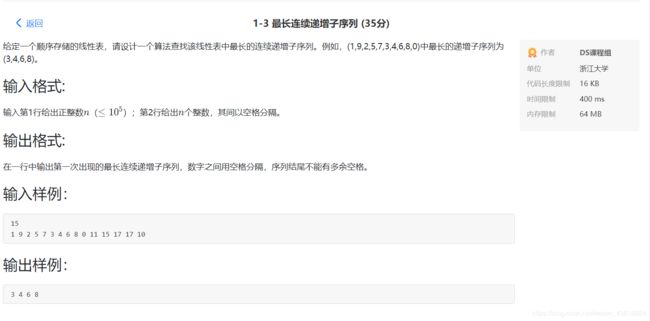
- 最长连续递增子序列
- 后缀式求值
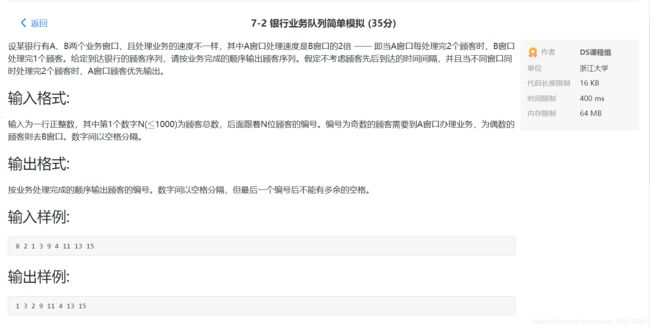
- 银行业务队列简单模拟
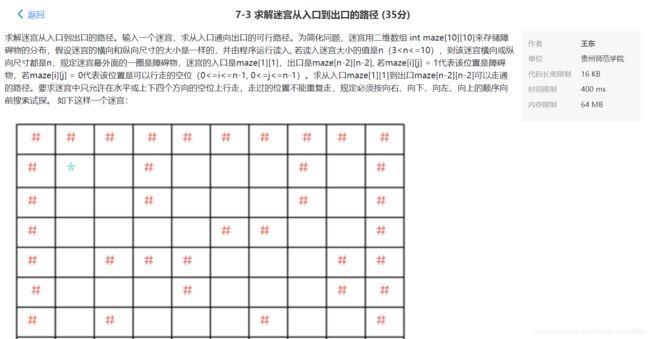
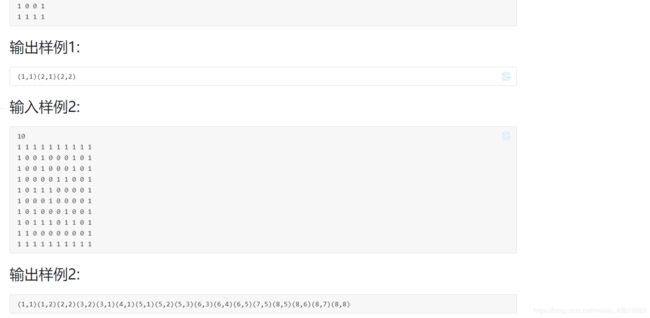
- 求解迷宫从入口到出口的路径
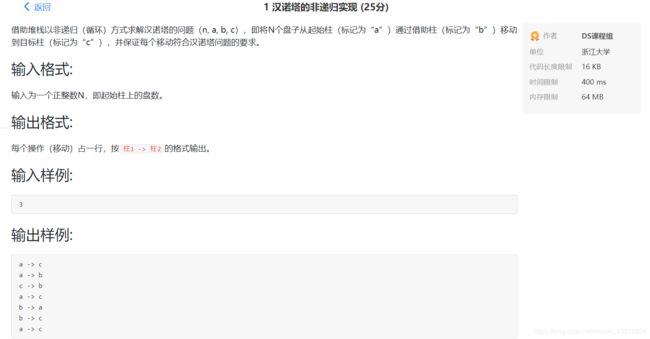
- 汉诺塔的非递归实现
- N皇后问题
- 表达式转换
- 堆栈模拟队列
- 奥运排行榜
- PAT排名汇总
- 抢红包
- 寻找大富翁
- 插入排序还是归并排序
- 根据后序和中序遍历输出先序遍历
- 树的遍历
- 列出叶结点
- 列出所有祖先结点
- 是否同一棵二叉搜索树
- 树种统计
- 二叉搜索树的最近公共祖先
- 朋友圈
- 秀恩爱分得快
- 文件传输
- 图着色问题
- 拯救007
- 列出连通集
- 哈利·波特的考试
- 旅游规划
- 镖局运镖
- 公路村村通
重排链表
#include 一元多项式的乘法与加法运算
#include 最长连续递增子序列
#include
}
}
if(temMax>Max){
Max = temMax;
start = newStart;
}
for(int i=start;i<start+Max-1;i++){
cout << a[i]<<" ";
}
cout << a[start+Max-1];
return 0;
}
后缀式求值
#include 银行业务队列简单模拟
#include 求解迷宫从入口到出口的路径
#include 汉诺塔的非递归实现
#include N皇后问题
在N * N的方格棋盘上,放置N个皇后,要求每个皇后不同行,不同列,不同左右对角线。 其中N不超过10。 要求:输出所有的解。 算法提示:用栈求解皇后问题。
输入格式:
输入N
输出格式:
逐行输出每一种解,用每个皇后的位置坐标表示,每个位置坐标之后均有一个空格符,输出最后一行为空行。
输入样例:
在这里给出一组输入。例如:
6
输出样例:
在这里给出相应的输出。例如:
1: (1,2) (2,4) (3,6) (4,1) (5,3) (6,5)
2: (1,3) (2,6) (3,2) (4,5) (5,1) (6,4)
3: (1,4) (2,1) (3,5) (4,2) (5,6) (6,3)
4: (1,5) (2,3) (3,1) (4,6) (5,4) (6,2)
#include 表达式转换
算术表达式有前缀表示法、中缀表示法和后缀表示法等形式。日常使用的算术表达式是采用中缀表示法,即二元运算符位于两个运算数中间。请设计程序将中缀表达式转换为后缀表达式。
输入格式:
输入在一行中给出不含空格的中缀表达式,可包含+、-、*、\以及左右括号(),表达式不超过20个字符。
输出格式:
在一行中输出转换后的后缀表达式,要求不同对象(运算数、运算符号)之间以空格分隔,但结尾不得有多余空格。
输入样例:
2+3*(7-4)+8/4
输出样例:
2 3 7 4 - * + 8 4 / +
#include 堆栈模拟队列
设已知有两个堆栈S1和S2,请用这两个堆栈模拟出一个队列Q。
所谓用堆栈模拟队列,实际上就是通过调用堆栈的下列操作函数:
int IsFull(Stack S):判断堆栈S是否已满,返回1或0;
int IsEmpty (Stack S ):判断堆栈S是否为空,返回1或0;
void Push(Stack S, ElementType item ):将元素item压入堆栈S;
ElementType Pop(Stack S ):删除并返回S的栈顶元素。
实现队列的操作,即入队void AddQ(ElementType item)和出队ElementType DeleteQ()。
输入格式:
输入首先给出两个正整数N1和N2,表示堆栈S1和S2的最大容量。随后给出一系列的队列操作:A item表示将item入列(这里假设item为整型数字);D表示出队操作;T表示输入结束。
输出格式:
对输入中的每个D操作,输出相应出队的数字,或者错误信息ERROR:Empty。如果入队操作无法执行,也需要输出ERROR:Full。每个输出占1行。
输入样例:
3 2
A 1 A 2 A 3 A 4 A 5 D A 6 D A 7 D A 8 D D D D T
输出样例:
ERROR:Full
1
ERROR:Full
2
3
4
7
8
ERROR:Empty
#include
char c;
getchar();//跳过第一行的回车
while(scanf("%c",&c)!=EOF){
if(c=='A'){
int d;
scanf("%d",&d);
push(d);
}
else if(c=='D')
pop();
else if(c=='T')
return 0;
}
}
奥运排行榜
每年奥运会各大媒体都会公布一个排行榜,但是细心的读者发现,不同国家的排行榜略有不同。比如中国金牌总数列第一的时候,中国媒体就公布“金牌榜”;而美国的奖牌总数第一,于是美国媒体就公布“奖牌榜”。如果人口少的国家公布一个“国民人均奖牌榜”,说不定非洲的国家会成为榜魁…… 现在就请你写一个程序,对每个前来咨询的国家按照对其最有利的方式计算它的排名。
输入格式:
输入的第一行给出两个正整数N和M(≤224,因为世界上共有224个国家和地区),分别是参与排名的国家和地区的总个数、以及前来咨询的国家的个数。为简单起见,我们把国家从0 ~ N−1编号。之后有N行输入,第i行给出编号为i−1的国家的金牌数、奖牌数、国民人口数(单位为百万),数字均为[0,1000]区间内的整数,用空格分隔。最后面一行给出M个前来咨询的国家的编号,用空格分隔。
输出格式:
在一行里顺序输出前来咨询的国家的排名:计算方式编号。其排名按照对该国家最有利的方式计算;计算方式编号为:金牌榜=1,奖牌榜=2,国民人均金牌榜=3,国民人均奖牌榜=4。输出间以空格分隔,输出结尾不能有多余空格。
若某国在不同排名方式下有相同名次,则输出编号最小的计算方式。
输入样例:
4 4
51 100 1000
36 110 300
6 14 32
5 18 40
0 1 2 3
输出样例:
1:1 1:2 1:3 1:4
#include
int q;
for(int i=0;i<m-1;i++){
cin >> q;
cout << Rank[q]+1 << ":" << style[q]+1<<" ";
}
cin >> q;
cout << Rank[q]+1 << ":" << style[q]+1;
return 0;
}
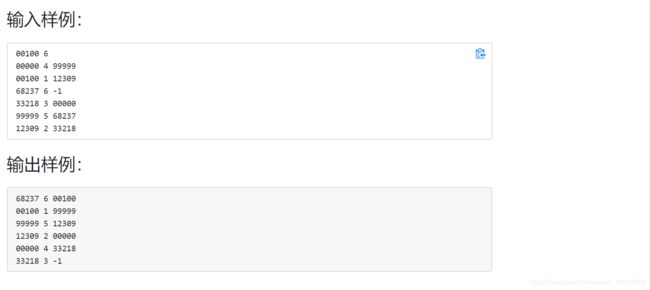
PAT排名汇总
计算机程序设计能力考试(Programming Ability Test,简称PAT)旨在通过统一组织的在线考试及自动评测方法客观地评判考生的算法设计与程序设计实现能力,科学的评价计算机程序设计人才,为企业选拔人才提供参考标准(网址http://www.patest.cn)。
每次考试会在若干个不同的考点同时举行,每个考点用局域网,产生本考点的成绩。考试结束后,各个考点的成绩将即刻汇总成一张总的排名表。
现在就请你写一个程序自动归并各个考点的成绩并生成总排名表。
输入格式:
输入的第一行给出一个正整数N(≤100),代表考点总数。随后给出N个考点的成绩,格式为:首先一行给出正整数K(≤300),代表该考点的考生总数;随后K行,每行给出1个考生的信息,包括考号(由13位整数字组成)和得分(为[0,100]区间内的整数),中间用空格分隔。
输出格式:
首先在第一行里输出考生总数。随后输出汇总的排名表,每个考生的信息占一行,顺序为:考号、最终排名、考点编号、在该考点的排名。其中考点按输入给出的顺序从1到N编号。考生的输出须按最终排名的非递减顺序输出,获得相同分数的考生应有相同名次,并按考号的递增顺序输出。
输入样例:
2
5
1234567890001 95
1234567890005 100
1234567890003 95
1234567890002 77
1234567890004 85
4
1234567890013 65
1234567890011 25
1234567890014 100
1234567890012 85
输出样例:
9
1234567890005 1 1 1
1234567890014 1 2 1
1234567890001 3 1 2
1234567890003 3 1 2
1234567890004 5 1 4
1234567890012 5 2 2
1234567890002 7 1 5
1234567890013 8 2 3
1234567890011 9 2 4
#include 抢红包
没有人没抢过红包吧…… 这里给出N个人之间互相发红包、抢红包的记录,请你统计一下他们抢红包的收获。
输入格式:
输入第一行给出一个正整数N(≤10
4
),即参与发红包和抢红包的总人数,则这些人从1到N编号。随后N行,第i行给出编号为i的人发红包的记录,格式如下:
KN
1
P
1
⋯N
K
P
K
其中K(0≤K≤20)是发出去的红包个数,N
i
是抢到红包的人的编号,P
i
(>0)是其抢到的红包金额(以分为单位)。注意:对于同一个人发出的红包,每人最多只能抢1次,不能重复抢。
输出格式:
按照收入金额从高到低的递减顺序输出每个人的编号和收入金额(以元为单位,输出小数点后2位)。每个人的信息占一行,两数字间有1个空格。如果收入金额有并列,则按抢到红包的个数递减输出;如果还有并列,则按个人编号递增输出。
输入样例:
10
3 2 22 10 58 8 125
5 1 345 3 211 5 233 7 13 8 101
1 7 8800
2 1 1000 2 1000
2 4 250 10 320
6 5 11 9 22 8 33 7 44 10 55 4 2
1 3 8800
2 1 23 2 123
1 8 250
4 2 121 4 516 7 112 9 10
输出样例:
1 11.63
2 3.63
8 3.63
3 2.11
7 1.69
6 -1.67
9 -2.18
10 -3.26
5 -3.26
4 -12.32
#include 寻找大富翁
胡润研究院的调查显示,截至2017年底,中国个人资产超过1亿元的高净值人群达15万人。假设给出N个人的个人资产值,请快速找出资产排前M位的大富翁。
输入格式:
输入首先给出两个正整数N(≤10
6
)和M(≤10),其中N为总人数,M为需要找出的大富翁数;接下来一行给出N个人的个人资产值,以百万元为单位,为不超过长整型范围的整数。数字间以空格分隔。
输出格式:
在一行内按非递增顺序输出资产排前M位的大富翁的个人资产值。数字间以空格分隔,但结尾不得有多余空格。
输入样例:
8 3
8 12 7 3 20 9 5 18
输出样例:
20 18 12
#include插入排序还是归并排序
根据维基百科的定义:
插入排序是迭代算法,逐一获得输入数据,逐步产生有序的输出序列。每步迭代中,算法从输入序列中取出一元素,将之插入有序序列中正确的位置。如此迭代直到全部元素有序。
归并排序进行如下迭代操作:首先将原始序列看成 N 个只包含 1 个元素的有序子序列,然后每次迭代归并两个相邻的有序子序列,直到最后只剩下 1 个有序的序列。
现给定原始序列和由某排序算法产生的中间序列,请你判断该算法究竟是哪种排序算法?
输入格式:
输入在第一行给出正整数 N (≤100);随后一行给出原始序列的 N 个整数;最后一行给出由某排序算法产生的中间序列。这里假设排序的目标序列是升序。数字间以空格分隔。
输出格式:
首先在第 1 行中输出Insertion Sort表示插入排序、或Merge Sort表示归并排序;然后在第 2 行中输出用该排序算法再迭代一轮的结果序列。题目保证每组测试的结果是唯一的。数字间以空格分隔,且行首尾不得有多余空格。
输入样例 1:
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
输出样例 1:
Insertion Sort
1 2 3 5 7 8 9 4 6 0
输入样例 2:
10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6
输出样例 2:
Merge Sort
1 2 3 8 4 5 7 9 0 6
#include 根据后序和中序遍历输出先序遍历
本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果,输出该树的先序遍历结果。
输入格式:
第一行给出正整数N(≤30),是树中结点的个数。随后两行,每行给出N个整数,分别对应后序遍历和中序遍历结果,数字间以空格分隔。题目保证输入正确对应一棵二叉树。
输出格式:
在一行中输出Preorder:以及该树的先序遍历结果。数字间有1个空格,行末不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
Preorder: 4 1 3 2 6 5 7
#include 树的遍历
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
#include 列出叶结点
对于给定的二叉树,本题要求你按从上到下、从左到右的顺序输出其所有叶节点。
输入格式:
首先第一行给出一个正整数 N(≤10),为树中结点总数。树中的结点从 0 到 N−1 编号。随后 N 行,每行给出一个对应结点左右孩子的编号。如果某个孩子不存在,则在对应位置给出 “-”。编号间以 1 个空格分隔。
输出格式:
在一行中按规定顺序输出叶节点的编号。编号间以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
8
1 -
0 -
2 7
5 -
4 6
输出样例:
4 1 5
#include 列出所有祖先结点
对于给定的二叉树,本题要求你按从上到下顺序输出指定结点的所有祖先结点。
输入格式:
首先第一行给出一个正整数 N(≤10),为树中结点总数。树中的结点从 0 到 N−1 编号。
随后 N 行,每行给出一个对应结点左右孩子的编号。如果某个孩子不存在,则在对应位置给出 “-”。编号间以 1 个空格分隔。
最后一行给出一个结点的编号i(0≤i≤N-1)。
输出格式:
在一行中按规定顺序输出i的所有祖先结点的编号。编号间以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 -
- 6
-
0 5
4 1
4
输出样例:
3 5
#include 是否同一棵二叉搜索树
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。最后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
#include 树种统计
随着卫星成像技术的应用,自然资源研究机构可以识别每一棵树的种类。请编写程序帮助研究人员统计每种树的数量,计算每种树占总数的百分比。
输入格式:
输入首先给出正整数N(≤10
5
),随后N行,每行给出卫星观测到的一棵树的种类名称。种类名称由不超过30个英文字母和空格组成(大小写不区分)。
输出格式:
按字典序递增输出各种树的种类名称及其所占总数的百分比,其间以空格分隔,保留小数点后4位。
输入样例:
29
Red Alder
Ash
Aspen
Basswood
Ash
Beech
Yellow Birch
Ash
Cherry
Cottonwood
Ash
Cypress
Red Elm
Gum
Hackberry
White Oak
Hickory
Pecan
Hard Maple
White Oak
Soft Maple
Red Oak
Red Oak
White Oak
Poplan
Sassafras
Sycamore
Black Walnut
Willow
输出样例:
Ash 13.7931%
Aspen 3.4483%
Basswood 3.4483%
Beech 3.4483%
Black Walnut 3.4483%
Cherry 3.4483%
Cottonwood 3.4483%
Cypress 3.4483%
Gum 3.4483%
Hackberry 3.4483%
Hard Maple 3.4483%
Hickory 3.4483%
Pecan 3.4483%
Poplan 3.4483%
Red Alder 3.4483%
Red Elm 3.4483%
Red Oak 6.8966%
Sassafras 3.4483%
Soft Maple 3.4483%
Sycamore 3.4483%
White Oak 10.3448%
Willow 3.4483%
Yellow Birch 3.4483%
#include 二叉搜索树的最近公共祖先
给定一棵二叉搜索树的先序遍历序列,要求你找出任意两结点的最近公共祖先结点(简称 LCA)。
输入格式:
输入的第一行给出两个正整数:待查询的结点对数 M(≤ 1 000)和二叉搜索树中结点个数 N(≤ 10 000)。随后一行给出 N 个不同的整数,为二叉搜索树的先序遍历序列。最后 M 行,每行给出一对整数键值 U 和 V。所有键值都在整型int范围内。
输出格式:
对每一对给定的 U 和 V,如果找到 A 是它们的最近公共祖先结点的键值,则在一行中输出 LCA of U and V is A.。但如果 U 和 V 中的一个结点是另一个结点的祖先,则在一行中输出 X is an ancestor of Y.,其中 X 是那个祖先结点的键值,Y 是另一个键值。如果 二叉搜索树中找不到以 U 或 V 为键值的结点,则输出 ERROR: U is not found. 或者 ERROR: V is not found.,或者 ERROR: U and V are not found.。
输入样例:
6 8
6 3 1 2 5 4 8 7
2 5
8 7
1 9
12 -3
0 8
99 99
输出样例:
LCA of 2 and 5 is 3.
8 is an ancestor of 7.
ERROR: 9 is not found.
ERROR: 12 and -3 are not found.
ERROR: 0 is not found.
ERROR: 99 and 99 are not found.
#include 朋友圈
某学校有N个学生,形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好,形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出,如果A和B是朋友,且B和C是朋友,则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。
输入格式:
输入的第一行包含两个正整数N(≤30000)和M(≤1000),分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息,其中学生从1~N编号:
第i个俱乐部的人数Mi(空格)学生1(空格)学生2 … 学生Mi
输出格式:
输出给出一个整数,表示在最大朋友圈中有多少人。
输入样例:
7 4
3 1 2 3
2 1 4
3 5 6 7
1 6
输出样例:
4
#include
}
}
int B[n+1]={0};
for(int i=1;i<=n;i++){
B[Find(a[i])]++;//cout << findHead(A,A[i])<
}
int maxn = 0;
for(int i=1;i<=n;i++){
maxn = max(maxn,B[i]);
}
cout << maxn;
}
秀恩爱分得快
古人云:秀恩爱,分得快。
互联网上每天都有大量人发布大量照片,我们通过分析这些照片,可以分析人与人之间的亲密度。如果一张照片上出现了 K 个人,这些人两两间的亲密度就被定义为 1/K。任意两个人如果同时出现在若干张照片里,他们之间的亲密度就是所有这些同框照片对应的亲密度之和。下面给定一批照片,请你分析一对给定的情侣,看看他们分别有没有亲密度更高的异性朋友?
输入格式:
输入在第一行给出 2 个正整数:N(不超过1000,为总人数——简单起见,我们把所有人从 0 到 N-1 编号。为了区分性别,我们用编号前的负号表示女性)和 M(不超过1000,为照片总数)。随后 M 行,每行给出一张照片的信息,格式如下:
K P[1] … P[K]
其中 K(≤ 500)是该照片中出现的人数,P[1] ~ P[K] 就是这些人的编号。最后一行给出一对异性情侣的编号 A 和 B。同行数字以空格分隔。题目保证每个人只有一个性别,并且不会在同一张照片里出现多次。
输出格式:
首先输出 A PA,其中 PA 是与 A 最亲密的异性。如果 PA 不唯一,则按他们编号的绝对值递增输出;然后类似地输出 B PB。但如果 A 和 B 正是彼此亲密度最高的一对,则只输出他们的编号,无论是否还有其他人并列。
输入样例 1:
10 4
4 -1 2 -3 4
4 2 -3 -5 -6
3 2 4 -5
3 -6 0 2
-3 2
输出样例 1:
-3 2
2 -5
2 -6
输入样例 2:
4 4
4 -1 2 -3 0
2 0 -3
2 2 -3
2 -1 2
-3 2
输出样例 2:
-3 2
#include文件传输
当两台计算机双向连通的时候,文件是可以在两台机器间传输的。给定一套计算机网络,请你判断任意两台指定的计算机之间能否传输文件?
输入格式:
首先在第一行给出网络中计算机的总数 N (2≤N≤10
4
),于是我们假设这些计算机从 1 到 N 编号。随后每行输入按以下格式给出:
I c1 c2
其中I表示在计算机c1和c2之间加入连线,使它们连通;或者是
C c1 c2
其中C表示查询计算机c1和c2之间能否传输文件;又或者是
S
这里S表示输入终止。
输出格式:
对每个C开头的查询,如果c1和c2之间可以传输文件,就在一行中输出"yes",否则输出"no"。当读到终止符时,在一行中输出"The network is connected.“如果网络中所有计算机之间都能传输文件;或者输出"There are k components.”,其中k是网络中连通集的个数。
输入样例 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
输出样例 1:
no
no
yes
There are 2 components.
输入样例 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
输出样例 2:
no
no
yes
yes
The network is connected.
#include 图着色问题
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式: 输出格式: 输入样例: 在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。) 设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。 输入格式: 输出格式: 输入样例 1: 给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。 输入格式: 输出格式: 输入样例: 哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。 现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。 输入格式: 输出格式: 输入样例: 有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。 输入格式: 输出格式: 输入样例: 镖局的运镖,就是运货(类似现在的物流)。镖局每到一个新地方开展业务,都需要对运镖途中的绿林好汉进行打点。好说话的打点费就比较低,不好说话的打点费就比较高。龙门镖局现在有一趟镖请你来规划路线,已知城市的地图,你需要选择一些道路进行疏通,以便镖局可以到达任意一个城市,要求花费的银子越少越好。 输入格式: 输出格式: 输入样例: 现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。 输入格式: 输出格式: 输入样例:
输入在第一行给出3个整数V(0
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4
输出样例:
Yes
Yes
No
No#include 拯救007
首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。
如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12
输出样例 1:
Yes
输入样例 2:
4 13
-12 12
12 12
-12 -12
12 -12
输出样例 2:
No#include 列出连通集
输入第1行给出2个整数N(0
按照"{ v
1
v
2
… v
k
}"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }#include 哈利·波特的考试
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70#include 旅游规划
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40#include 镖局运镖
第一行有两个数n和m,n表示有n个城市(编号从1到n),m表示有m条道路。接下来m行,每行形如“a b c”用来表示一条道路,意思是城市a到城市b连通且打点需要花费的银子数是c。
若通过打点能抵达所有城市,则输出最少需要花费的银子总数。若不能抵达所有的城市则输出“impossible”。
3 3
1 2 1
1 3 2
2 3 4
输出样例:
3#include 公路村村通
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12#include