梯度下降法 及其Python实现

什么是梯度下降法

梯度下降 Gradient Descent：本身不是一个机器学习的算法，而是一种基于搜索的最优化方法。
作用：最小化一个损失函数。
梯度上升法：最大化一个效用函数。

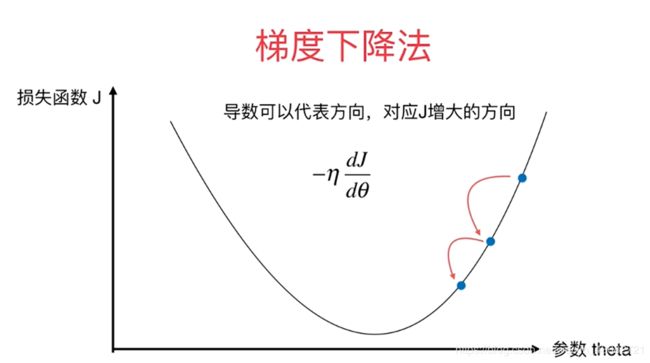
• η称为学习率（learning rate）
• η的取值影响获得最优解的速度：如当η过小，需要经过非常多次的迭代
• η取值不合适，甚至得不到最优解：如当η过大，可能不能到达使目标更小的点
• η是梯度下降法的一个超参数

初始点：

• 并不是所有函数都有唯一的极值点
  初始点对结果有影响，如下图所示：
  
  解决方案：
• 多次运行，随机化初始点
• 梯度下降法的初始点也是一个超参数

而线性回归法的损失函数具有唯一最优解。

线性回归中的梯度下降法

线性回归的目标函数以及梯度：

实现线性回归中的梯度下降法

将下面的方法写在LinearRegression.py中，作为线性回归的一种训练方式：

def fit_gd(self,X_train,y_train,eta = 0.01, n_iters = 1e4):
    '''根据训练数据集X_train,y_train，使用梯度下降法训练线性回归模型'''
    assert X_train.shape[0] == y_train.shape[0] , 'the size of X_train must equal to the size of y_train'
    
    def J(theta,X_b,y):
    '''计算损失函数'''
      try:
        return np.sum((y - X_b.dot(theta))**2) / len(y)
      except:
        return float('inf')
      
    def dJ(theta,X_b,y):
    '''计算损失函数在每一个特征上的导数，即为梯度'''
      res = np.empty(len(theta))
      res[0] = np.sum(X_b.dot(theta) - y)
      for i in range(1,len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
      return res * 2 / len(X_b)

    def gradient_descent(X_b,y,initial_theta,eta,n_iters = 1e4,epsilon = 1e-8):
    '''计算随着梯度下降，最终得到的theta'''
      theta = initial_theta
      cur_iter = 0
      while cur_iter < n_iters:
        gradient = dJ(theta,X_b,y)
        last_theta = theta
        theta = theta - eta * gradient
        if(abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < epsilon):
          break
        cur_iter += 1 
      return theta

    X_b = np.hstack([np.ones((len(X_train),1)),X_train])
    initial_theta = np.zeros(X_b.shape[1])
    self._theta = gradient_descent(X_b,y_train,initial_theta,eta,n_iters)
    self.interception_ = self._theta[0]
    self.coef_ = self._theta[1:]

    return self

使用方式为：

#数据
x2 = 2 * np.random.random(size = 100)
y2 = x2 * 3. + 4. + np.random.normal(size = 100)
x2 = x2.reshape(-1,1)

reg2 = LinearRegression()
reg2.fit_gd(x2,y2)
print(reg2.coef_)
print(reg2.interception_)

梯度下降法的向量化和数据标准化

梯度下降法的向量化

将所要求的梯度向量化，如下：

代码：

def dJ(theta,X_b,y):
      # res = np.empty(len(theta))
      # res[0] = np.sum(X_b.dot(theta) - y)
      # for i in range(1,len(theta)):
      #   res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
      # return res * 2 / len(X_b)
      return X_b.T.dot(X_b.dot(theta) - y) * 2 / len(y)

数据归一化

如果数据不属于同一个量级，在梯度变化的过程中，同一步长对多个特征的影响不同，这导致目标函数可能不能收敛。因此需要进行数据的归一化。

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)

正规方程法与梯度下降法

正规化方程不需要进行数据归一化，而梯度下降法需要进行数据归一化。
当数据的特征数大时，梯度下降法相对于正规方程法而言，更为省时。

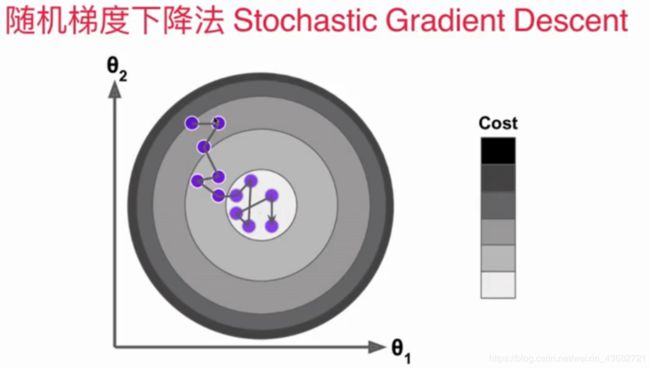
随机梯度下降法

随机梯度下降代码：

def fit_sgd(self,X_train,y_train,n_iters = 5,t0 = 5,t1 = 50):
      '''根据训练数据集使用梯度下降法训练线性回归模型'''
      assert X_train.shape[0] == y_train.shape[0],'the size of X_train must equal to the size of y_train'
      assert n_iters >= 1  
    
      def dJ_sgd(theta,X_b_i,y_i):
        return X_b_i * (X_b_i.dot(theta) - y_i)*2.
      
      def sgd(X_b ,y ,initial_theta,n_tiers,t0 = 5,t1 = 50):
        def learning_rate(t):
          return t0 /(t +t1)

        theta = initial_theta 
        m = len(X_b)

        for cur_iter in range(n_iters):
          indexes = np.random.permutation(m)
          X_b_new = X_b[indexes]
          y_new = y[indexes]
          for i in range(m):
            gradient = dJ_sgd(theta,X_b_new[i],y_new[i])
            theta = theta - learning_rate(cur_iter * m + i) * gradient

        return theta
      X_b = np.hstack([np.ones((len(X_train),1)),X_train])
      initial_theta = np.random.randn(X_b.shape[1])
      self._theta = sgd(X_b,y_train,initial_theta,n_iters,t0,t1)
      self.interception_ = self._theta[0]
      self.coef_ = self._theta[1:]

      return self

测试：

reg3 = LinearRegression()
reg3.fit_sgd(X3,y3, n_iters = 2)
print(reg3.coef_)
print(reg3.interception_)

scikit-learn中的随机梯度下降法

scikit-learn中随机梯度下降法的使用：

from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter = 100)
sgd_reg.fit(X_train_standard,y_train)
sgd_reg.score(X_test_standard,y_test)