python数据分析与挖掘实战 之笔记2

《python数据分析与挖掘实战》学习笔记2

• 经过前面章节的分析，即对数据进行探索和预处理，得到了处理后的数据。根据所得到的数据建立分类与预测、聚类分析、关联规则、时序模式、和偏差检测等模型，提取数据中蕴含的有价值的信息。
• 后面会在weka平台上实现数据挖掘的一些功能。
• 下面就将对这部分知识做大致的介绍。

1、分类与预测

1.1 回归分析

———————————————————————————————————
线性回归——因、自变量是线性关系，对一个或多个自、因变量线性建模，用最小二乘法求系数。
非线性回归——因、自变量是非线性，非线性建模。
Logistic回归——因变量为0或1二分类，广义线性回归特例，利用Logistic函数将因变量控制0-1内表示取值为1的概率。
岭回归——参与建模的自变量间具有多重共线性，用改进的最小二乘法估计。
主成分回归——自变量间含有多重共线性，根据PCA提出，是参数估计的一种有偏估计。
———————————————————————————————————

本小节只对二分类Logistic回归模型的相关原理进行介绍：

• （1）该模型的因变量只有0-1两个取值，假设在n个独立自变量$x_1,x_2,...,x_n$作用下，记y取1的概率为p，p=P(y=1|x)，取0的概率是1-p，取1和取0的概率之比为$\frac{p}{1-p}$,称为事件的优势比（odds）,简称os；对其自然对数，$logit(p)=ln(\frac{p}{1-p})$，令其等于z，则$p=\frac{1}{1+e^{-z}}$，该表达式即为logistic函数。
• 当p在（0,1）时，odds的取值为（0，$\infty$），$ln(\frac{p}{1-p})$的取值范围为（$-\infty$，$\infty$）。
• 回归模型为：
  $$ln(\frac{p}{1-p})={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p+\epsilon$$
• （2）建模步骤：
  ①筛选特征。采用稳定性选择方法中的随机逻辑回归进行特征筛选。
  ②建立回归方程。
  ③估计回归系数。
  ④进行模型检验。算出正确率，KS值、ROC曲线等。
  ⑤预测。
• 下面的模型是对某银行降低贷款拖欠率的数据进行预测的原始数据和代码：
  

#-*- coding: utf-8 -*-
#逻辑回归，自动建模
import pandas as pd
#参数初始化
filename =r'E:\..\demo\data\bankloan.xls'
data = pd.read_excel(filename)
x = data.iloc[:,:8].as_matrix()
y = data.iloc[:,8].as_matrix()
from sklearn.linear_model import LogisticRegression as LR
from sklearn.linear_model import RandomizedLogisticRegression as RLR 
rlr = RLR() #稳定性选择方法中的随机逻辑回归进行特征筛选
rlr.fit(x, y) #训练模型
rlr.get_support() #获取筛选结果
print('特征筛选结束')
print('有效特征为：%s' % ','.join(data.iloc[:,:8].columns[rlr.get_support()]))
x=data[data.iloc[:,:8].columns[rlr.get_support()]].as_matrix()#筛选好特征
lr = LR() #建立逻辑回归模型
lr.fit(x, y) #用筛选后的特征数据来训练模型
print('逻辑回归模型训练结束')
print('模型的平均正确率为：%s' % lr.score(x, y))

结果为：
特征筛选结束
有效特征为：工龄,地址,负债率,信用卡负债
逻辑回归模型训练结束
模型的平均正确率为：0.814285714286
———————————————————————————————————

1.2 决策树

———————————————————————————————————
决策树是一种基本的分类与回归方法，一般多用于分类问题中，表示基于特征对实例进行分类的过程，可以认为是if-then规则的集合，或者说是定义在特征空间与类空间上的条件概率分布。
其主要分为2个大的模块，学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型；预测时，对于给出的未知数据，利用之前所建立的决策树模型进行分类预测。
具体包括3个步骤：特征选择；决策树生成；决策树剪枝。
决策树算法的分类：

• 1、ID3算法：其核心是在决策树的各级节点上，使用信息增益方法作为属性的选择标准，来帮助确定生成每个节点时所应采用的合适属性，适用于离散型数据。
• 2、C4.5算法：是使用信息增益率来选择节点属性，ID3只适用于离散的属性描述，而C4.5既能够处理离散的描述属性，也可以处理连续的描述属性。
• 3、CART算法：是一种十分有效地非参数分类和回归方法，通过构建树、修剪树、评估树来构建一个二叉树。当终节点是连续变量时，该树为回归树；当终节点是分类变量时，该树为分类树。

ID3计算步骤：（1）对当前样本集合，计算所有属性的信息增益；（2）选择信息增益最大的属性作为测试属性，把测试属性取值相同的样本划为同一子样本集；（3）若子样本集的类别属性只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处；否则对子样本集递归调用本算法。

原理为：（1）总的信息熵，共m个类别。其概率为给类别个数占总个数的比值。
$$I(s_1,s_2,...,s_m)=-\sum _i^m{P}_{i}lo{g}_2(P_i)$$
（2）计算各属性的信息熵值：A属性的信息熵值。
$$E(A)=\sum _{j=i}^k\frac{s_{1j}+s_{2j}+...+s_{mj}}{s}I(s_{1j},...,s_{mj})$$
（3）计算该属性划分样本集的信息增益为：
$$Gain(A)=I(s_1,s_2,...,s_m)-E(A)$$
其中E(A)越小越好，Gain(A)越大越好，即说明选择A属性对于分类所提供的信息越大，其对分类的不确定程度越小。

举例对某餐饮企业的相关销售数据，分析出对销量有影响的因素。

• 总共三个属性：①天气：分为好与坏；②是否周末：分为是与否；③是否促销：分为是与否；最终销量：按平均值大小划分，>均值为高，<均值为低。
  数据如下：共34个数据。
  
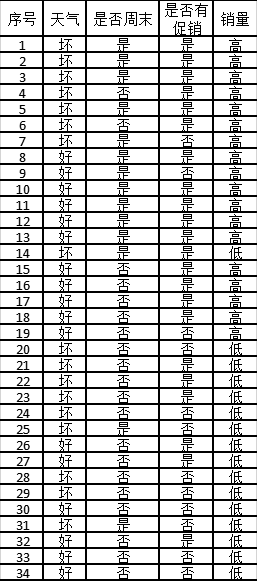
• 采用ID3算法构建决策树模型的具体步骤如下所示：
  1）计算总的信息熵：销量高的为18个，低的为16个。
  2）计算各属性的信息熵：
  3）计算信息增益值，选择最高的值作为分类对象。
  
  ps：看来需要练字了或者换只笔吧。
• 代码如下所示：

# 决策树算法预测销量高低代码
import pandas as pd
filename=r'E:...\Python数据分析与挖掘实战\chapter5\demo\data\sales_data.xls'  #文件路径根据自己设置，可以是绝对的，也可以是相对的。
data=pd.read_excel(filename,index_col='序号')
data[data=='好']=1
data[data=='是']=1
data[data=='高']=1
data[data !=1]=-1#将类别标签数据转化为数据，用1表示好，是，高，用-1表示坏，否，低
x=data.iloc[:,:3].as_matrix().astype(int)
y=data.iloc[:,3].as_matrix().astype(int)
from sklearn.tree import DecisionTreeClassifier as DTC
dtc=DTC(criterion='entropy')#基于信息熵建立决策树
dtc.fit(x,y)#训练模型
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO#导入相关函数，可视化决策树
x=pd.DataFrame(x)
with open("tree.dot",'w') as f:
    f=export_graphviz(dtc,feature_names=x.columns,out_file=f)
    #dot -Tpdf tree.dot -o tree.pdf #将结果可视化，不知道为什么不行
    #dot -Tpng tree.dot -o tree.pdf

结果为：


———————————————————————————————————

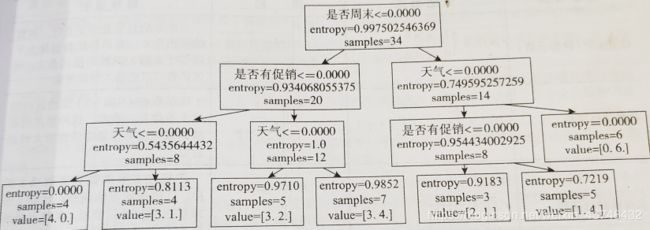
1.3 人工神经网络

———————————————————————————————————
各类神经网络算法

• 1）BP神经网络：是一种按误差逆传播算法训练的多层前馈网络，学习算法是西格玛学习规则，是目前应用最广泛的神经网络模型之一。
• 2）LM神经网络：是基于梯度下降法和牛顿法结合的多层前馈网络，迭代次数少，收敛速度快，精确度高。
• 3）RBF径向基神经网络：RBF网络能够以任意精度逼近任意连续函数，从输入层到隐含层的变换是非线性的，而从隐含层到输出层的变换是线性的，特别适合解决分类问题。
• 4）FNN模糊神经网络：FNN模糊神经网络是具有模糊权系数或者输入信号是模糊量的神经网络，是模糊系统与神经网络相结合的产物，它汇聚了神经网络与模糊系统的优点，集联想、识别、自适应及模糊信息处理于一体。
• 5）GMDH神经网络：也称为多项式网络，是前馈神经网络中常用的一种用于预测的神经网络，特点是网络结构不固定，而且在训练过程中不断改变。
• 6）ANFIS自适应神经网络：神经网络镶嵌在一个全部模糊的结构之中，在不知不觉中向训练数据学习，自动产生、修正并高度概括出最佳的输入与输出变量的隶属函数以及模糊规则；另外，神经网络的各层结构与参数也都具有了明确的、易于理解的物理意义。

BP算法的学习过程由信号的正向传播与误差的逆向传播两个过程组成。正向传播时，输入信号经过隐层的处理后，传向输入层。若输出层节点未能得到期望的输出，则转入误差的逆向传播阶段，将输出误差按某种子形式，通过隐层向输入层返回，从而获得各层单元的参考误差或称误差信号，作为修改各单元权值的依据。此过程一直进行到网络输出的误差逐渐减少到可接受的程度或达到设定的学习次数为止。
神经网络算法预测销量高低的相关代码及结果：

import pandas as pd
filename=r'E:\...\Python数据分析与挖掘实战\chapter5\demo\data\sales_data.xls'
data=pd.read_excel(filename,index_col='序号')
data[data=='好']=1
data[data=='是']=1
data[data=='高']=1
data[data !=1]=0#将类别标签数据转化为数据，用1表示好，是，高，用0表示坏，否，低
x=data.iloc[:,:3].as_matrix().astype(int)
y=data.iloc[:,3].as_matrix().astype(int)
# from tensorflow import
from keras.models import Sequential
from keras.layers.core import Dense,Activation
model=Sequential()#建立模型
model.add(Dense(input_dim=3,output_dim=10))
model.add(Activation('relu'))#用relu函数作为激活函数，提高准确度
model.add(Dense(input_dim=10,output_dim=1))
model.add(Activation('sigmoid'))#由于是0-1输出，用sigmoid函数作为激活函数
model.compile(loss='binary_crossentropy',optimizer='adam',class_mode='binary')#编译模型，指定损失函数为binary_crossentropy,模式为binary，求解方法为adam。
model.fit(x,y,nb_epoch=1000,batch_size=10)#训练模型，学习1000次
yp=model.predict_classes(x).reshape(len(y))#分类预测
# from cm_plot import *#导入混淆矩阵可视化函数
# cm_plot(y,yp).show()
def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
    cm = confusion_matrix(y, yp)  # 混淆矩阵
    import matplotlib.pyplot as plt
    plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
    plt.colorbar()  # 颜色标签
    for x in range(len(cm)):  # 数据标签
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
    plt.ylabel('True label')  # 坐标轴标签
    plt.xlabel('Predicted label')  # 坐标轴标签
    return plt
cm_plot(y, yp).show()

结果报错：没能得到解决。后续在更改。

———————————————————————————————————

1.4 分类与预测算法评价

———————————————————————————————————

• 1）采用均方误差或者均方根误差来衡量，模型预测的效果。
  $$MSE=\frac{1}{n}\sum _{i=1}^n{E}_i^2=\frac{1}{n}\sum _{i=1}^n(Y_i-{\hat{Y}}_i{)}^2$$
  该值是预测误差平方之和的平均数，避免了正负误差不能相加的问题。其误差的平方加强了数值大的误差在指标中的作用，从而提高了这个指标的灵敏性，有助于判断预测结果的好坏。
• 2）其次是均方根误差。在均方误差的基础上，求其平方根，也可称为标准误差，代表了预测值的离散程度，其值越小越好。
  $$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{E}_i^2}=\sqrt{\frac{1}{n}\sum _{i=1}^n(Y_i-{\hat{Y}}_i{)}^2}$$
• 3）识别准确度：
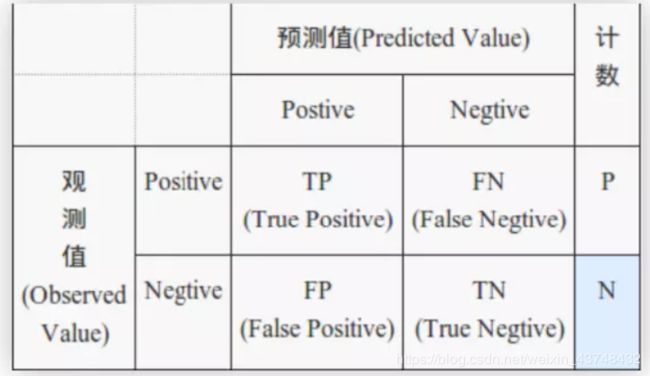
  TP：将正类预测为正类数
  TN：将正类预测为负类数
  FP：将负类预测为正类数
  FN：将负类预测为负类数
  准确率：$$accuracy=\frac{TP+FN}{TP+TN+FP+FN}\times 100$$
• 4）识别精确率
  $$P=\frac{TP}{TP+FP}$$
  反馈率：$$R=\frac{TP}{TP+TN}$$
• 5）ROC曲线
  
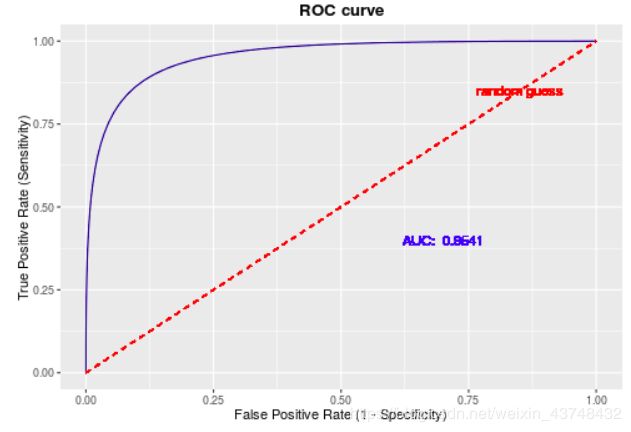
  该曲线的横坐标轴为假阳性率（FPR），N为真实负样本的个数，$$FPR=\frac{FP}{N}$$
  纵坐标为真阳性率（TPR）,P为真实正样本的个数，$$TPR=\frac{TP}{P}$$
• 6）混淆矩阵
  
  —————————————————————————————

2、聚类分析

实例问题阐述：如餐饮企业
（1）通过客户的消费行为挖掘有价值的客户群；
（2）如何合理对菜品进行分析，挖掘毛利润较高的菜品。

• 常用的聚类分析算法有：
  ①K-Means算法： K-均值聚类也称快速聚类法，在最小化误差函数的基础上将数据划分为预定的类数K。原理简单，便于处理大量数据。
  ②K-中心点：K-均值对于孤立点敏感。K-中心点算法不采用簇中对象的平均值作为簇中心，而选用簇中离平均值最近的对象作为簇中心。
  ③系统聚类：也称多层次聚类，分类的单位由高到低呈树形结构，且所处的位置越低，其所包含的对象就越少，但这些对象间的共同特征越多。只适合在小数据量的时候使用，数据量大的时候速度会非常慢。

本次分析主要运用了K-Means聚类算法，所以对其做一个大致的阐述。K-Means聚类算法是一种典型的基于距离的非层次聚类算法，在保证最小化误差函数的基础上将数据划分为预定的类数K，采用距离作为相似性的评价指标，也就是说两个对象的距离越近，其相似度就越高。

• 实现聚类的步骤：
  ①将所得到的数据进行预处理，填补缺失值、数据标准化等；
  ②运用相应的算法在软件中加以实现；
  ③得到最终的聚类结果；
  ④评价分析相应的结果。
• K-Means聚类算法过程：
  ①首先从N个样本中随机选取K个对象作为初始的聚类中心；
  ②分别计算每个样本到各个聚类中心的距离（欧氏距离），将对象分配到距离最小的类中；
  ③在所有对象都分配完后，重新产生K个类的聚类中心；
  ④若③中聚类中心有所变化，则重复操作②过程，否则进入⑤；
  ⑤当所有的质心不在发生变化，则停止，输出相应的聚类结果。
• 其中欧式距离的计算公式，两个点A(x1,y1),B(x2,y2)，求解两点之间的距离：
  
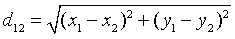
  选择其中误差平方和最小的值作为聚类的目标函数，输出其分类结果。

2.1 实际操作：

本题选取了以餐饮客户消费情况为例的940个客户，3个消费特征为研究背景的数据，其中第一个特征为最近一次消费的时间间隔，第二个为消费频率，第三个为消费的总金额。根据这些数据将客户划分为不同的客户群，并对所得到的客户群体进行价值评价。

• ①选取相应数据。某餐饮客户的消费行为数据，如下部分数据：
  
• ②使用以pycharm为编辑环境的python3.7进行分析，导入sklearn.cluster中的kmeans模块，对数据进行聚类，大致预设分为3类，对数据迭代600次。并绘制相应的概率密度图，以便更直观的得到每个聚类成员的大致分布情况。
  具体代码如下所示。
  model = KMeans(n_clusters=k, n_jobs=4, max_iter=iteration, random_state=1234) # 分为k类，k为3,并发数4
  model.fit(data_zs) # 开始聚类

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 参数初始化
inputfile = 'consumption_data.xls'  # 销量及其他属性数据
outputfile = 'data_type.xls'  # 保存结果的文件名
k = 3  # 聚类的类别
iteration = 600  # 聚类最大循环次数
data = pd.read_excel(inputfile, index_col='Id')  # 读取数据
data_zs = 1.0 * (data - data.mean()) / data.std()  # 数据标准化

model = KMeans(n_clusters=k, n_jobs=4, max_iter=iteration, random_state=1234)  # 分为k类，并发数4
model.fit(data_zs)  # 开始聚类

# 简单打印结果
r1 = pd.Series(model.labels_).value_counts()  # 统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_)  # 找出聚类中心
r = pd.concat([r2, r1], axis=1)  # 横向连接（0是纵向），得到聚类中心对应的类别下的数目
r.columns = list(data.columns) + ['类别数目']  # 重命名表头
print(r)

# 详细输出原始数据及其类别
r = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)  # 详细输出每个样本对应的类别
r.columns = list(data.columns) + ['聚类类别']  # 重命名表头
r.to_excel(outputfile)  # 保存结果

def density_plot(data):  # 自定义作图函数
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    p = data.plot(kind='kde', linewidth=2, subplots=True, sharex=False)
    [p[i].set_ylabel(u'密度') for i in range(k)]
    plt.legend()
    return plt

pic_output = 'pd'  # 概率密度图文件名前缀
for i in range(k):
    density_plot(data[r[u'聚类类别'] == i]).savefig(u'%s%s.png' % (pic_output, i))

• ③得到相应的聚类结果。如下所示：
  
  从上面的结果可以看出，将940名顾客分为了三类，第一类有40个人，第二类有341个，第三类有559个。
  
  图1 第一个聚类成员的概率密度图
  从图1可以看出，第一类的R间隔相对较大，主要集中在30-80天；消费次数集中在0-15次；消费金额集中在0-2000元之间。
  
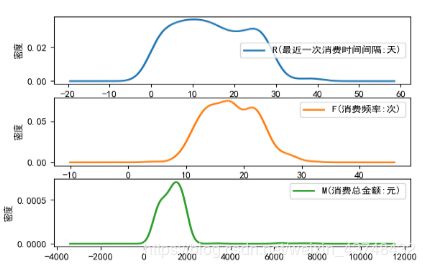
  图2第二个聚类成员的概率密度图
  从图2 可以看出，第二类的R间隔相对较小，主要集中在0-30天；消费次数集中在10-25次；消费金额集中在30-2000元之间。
  
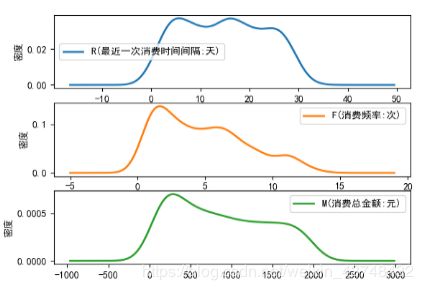
  图3 第三个聚类成员的概率密度图
  从图3可以看出，第三类的R主要分布在0-30天；消费次数集中在0-15次；消费金额集中在0-2000元之间。
  为了更直观的观察聚类的结果：可以利用TSNE工具将其可视化为以下图形：代码也如下所示。

import pandas as pd
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

# 参数初始化
inputfile = 'consumption_data.xls'  # 销量及其他属性数据
inputfile1 = 'data_type.xls'
data = pd.read_excel(inputfile, index_col = 'Id')  # 读取数据
data_zs = 1.0*(data - data.mean())/data.std()
r = pd.read_excel(inputfile1,index_col='Id')

tsne = TSNE(random_state=105)
tsne.fit_transform(data_zs)  # 进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index = data_zs.index)  # 转换数据格式

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 不同类别用不同颜色和样式绘图
d = tsne[r['聚类类别'] == 0]
plt.plot(d[0], d[1], 'r+',label='低价值客户群', linewidth=2)
d = tsne[r['聚类类别'] == 1]
plt.plot(d[0], d[1], 'yo',label="高价值客户群", linewidth=2)
d = tsne[r['聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*',label="一般价值客户群", linewidth=2)
plt.legend()
plt.show()

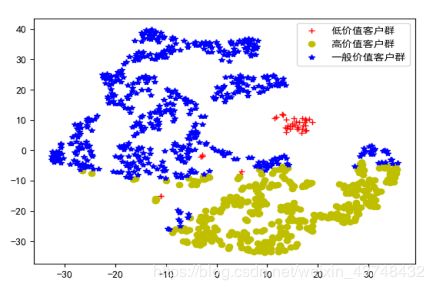
图4聚类效果图
从上图可以看出，大部分都聚合在了一起，聚合效果较好。

• 综合分析以上结果，可以得知，所有客户群中，第一类消费时间间隔较大，消费次数也较少，消费金额也较低，这类客户属于低消费型，价值较低的客户群体。而第二类客户群消费比较频繁，且消费金额也较高，是高消费、高价值人群。第三类消费时间间隔、次数、金额都属于中等状态，其表示一般的价值客户群体。

为了进一步确定其分类的准确性，在spss21.0中也进行了相关的聚类操作，其中采用k-means聚类和系统聚类的结果都是相同的，但与上述的python结果有所出入。
SPSS21.0聚类过程和结果如下所示：
①分析—分类—k-均值/系统聚类。

②迭代选择600次，产生3类。
③结果如下所示：


从上面的结果来看，与python中的结果有所出入，且从方差分析表的结果来看，其结果更为显著，准确性更高一些。

3、关联规则

3.1定义：

关联规则分析又称购物篮分析，最早为了发现超市销售数据库中不同的商品之间的关联关系。例如：某顾客在购买了面包之后，很可能也会购买牛奶；购买了啤酒的顾客很可能也会购买尿不湿等。这样就可以提取其中的关联规则：“面包—牛奶”，“啤酒—尿不湿”。前项—后项的规则，这时，商店管理者就可制定相应的政策，如，降低面包的售价，适当提高牛奶的售价，进而增加超市整体的利润。

3.2常用关联规则算法：

1、Apriori：关联规则最常用的挖掘频繁项集的算法，核心思想是通过连接产生选项及其支持度然后通过剪枝生成频繁项集。
2、FP-Tree：针对Apriori固有的多次扫描事务数据集的缺项，提出不产生候选频繁项集的方法。
3、Eclat：是一种深度优先算法，采用垂直数据表示形式，在概念和理论的基础上利用基于前缀的等价关系将搜索空间划分为较小的子空间。
4、灰色关联法：分析和确定各因素之间的影响程度或是若干子因素对主因素的贡献度进行分析的方法。
下面重点阐述Apriori算法的应用。

3.３Apriori算法的原理及应用

关联规则：形如X->Y的蕴涵表达式，其中X和Y是不相交的项集。关联规则的强度可以用支持度（support）、置信度（confidence）、提升度（lift）度量。

• 支持度：确定规则可以用于给定数据集的频繁程度。通俗来讲就是一个事务出现的次数与其给定数据集的占比就为支持度。
  S(X→Y)=P(X∪Y)/N
• 置信度：确定Y在包含X的事务中出现的频繁程度。即X与Y同时出现与X出现的占比情况为置信度。
  C(X→Y)=P(X∪Y)/P(X)
• 提升度：表示“包含 X的事务中同时包含 Y 的事务的比例”与“包含 Y 的事务的比例”的比值。
  L(P(X&Y)/P(X))/P(Y)=P(X&Y)/P(X)/P(Y)
  提升度反映了关联规则中的X与Y的相关性，提升度>1且越高表明正相关性越高，提升度<1且越低表明负相关性越高，提升度=1表明没有相关性。
• 一般大多数关联规则挖掘算法通常采用的策略是，将关联规则挖掘任务分解为如下两个主要的子任务。
  ①产生频繁项集：其目标是发现满足最小支持度阈值的所有项集，这些项集称作频繁项集（frequent itemset）。
  ②规则的产生：其目标是从上一步发现的频繁项集中提取所有高置信度的规则，这些规则称作强规则（strong rule）。
• 由于频繁项集产生所需的计算开销远大于产生规则所需的计算开销，我们必须设法降低产生频繁项集的计算复杂度。此时我们可以利用支持度对候选项集进行剪枝，也就是Apriori算法，或者其他的一些算法。
• Apriori算法：其功能主要是为了获得频繁集。其采用广度优先的搜索策略，自底向上的遍历思想，遵循首先产生候选集进而获得频繁集的思路。
  基本思想是：首先扫描数据集，统计数据集中交易的数量和各个不同的1项集出现的次数；然后根据最小支持度原则得到所有的频繁1项集，即L1，在此基础上找到频繁2项集，即L2，持续该步骤直到不会出现新的频繁项集。即连续步与剪枝步相结合。

3.3.1 实例应用

• 1、选择数据
  由于书中所选数据未能找到完整的数据集。
  在网上重新选择了一个关于某超市的某段时间的一个销售数据，部分数据如下，共1000条记录，18个特征。主要的交易购买的产品有水果和蔬菜、肉、奶制品、蔬菜罐头、肉罐头、冷冻食品、啤酒、葡萄酒、苏打水、鱼、纺织品等数据。前面是消费者的一些相关的信息特征。该数据集命名为：shopping_data.xls。
  主要的交易购买的产品有水果和蔬菜、肉、奶制品、蔬菜罐头、肉罐头、冷冻食品、啤酒、葡萄酒、苏打水、鱼、纺织品等数据。
  
• 2、定义相应的apriori算法

# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
def connect_string(x, ms):
    x = list(map(lambda i:sorted(i.split(ms)), x))
    l = len(x[0])
    r = []
    for i in range(len(x)):
        for j in range(i,len(x)):
            if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
                r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
    return r

#寻找关联规则的函数
def find_rule(d, support, confidence, ms = u'--'):
    result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果
  
    support_series = 1.0*d.sum()/len(d) #支持度序列
    column = list(support_series[support_series > support].index) #初步根据支持度筛选
    k = 0
	
    while len(column) > 1:
    	k = k+1
    	print(u'\n正在进行第%s次搜索...' %k)
    	column = connect_string(column, ms)
    	print(u'数目：%s...' %len(column))
    	sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数
    	
    	#创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。
    	d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T
    	
    	support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
    	column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
    	support_series = support_series.append(support_series_2)
    	column2 = []
    	
    	for i in column: #遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？
    	    i = i.split(ms)
    	    for j in range(len(i)):
    		    column2.append(i[:j]+i[j+1:]+i[j:j+1])
    	
    	cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列
     
    	for i in column2: #计算置信度序列
    	    cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
    	
    	for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
    	    result[i] = 0.0
    	    result[i]['confidence'] = cofidence_series[i]
    	    result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]
  
    result = result.T.sort_values(['confidence','support'], ascending = False) #结果整理，输出
    print(u'\n结果为：')
    print(result)
    return result

将上述代码命名为：apriori.py.

• 3、导入数据，应用apriori算法提取相应的规则：
  最小支持度设置为0.1，最小置信度设置为0.5。

# -*- coding: utf-8 -*-
from __future__ import print_function
import pandas as pd
from apriori import *  # 导入自行编写的apriori函数

inputfile = '../data/shopping_data.xls'
outputfile = '../tmp/apriori_rules1.xls'  # 结果文件
data = pd.read_excel(inputfile, header = None)

print(u'\n转换原始数据至0-1矩阵...')
ct = lambda x : pd.Series(1, index=x[pd.notnull(x)])  # 转换0-1矩阵的过渡函数
b = map(ct, data.as_matrix())  # 用map方式执行
data = pd.DataFrame(list(b)).fillna(0)  # 实现矩阵转换，空值用0填充
print(data)
print(u'\n转换完毕。')
del b  # 删除中间变量b，节省内存

support = 0.1 # 最小支持度
confidence = 0.5  # 最小置信度
ms = '---'  # 连接符，默认'--'，用来区分不同元素，如A--B。需要保证原始表格中不含有该字符

find_rule(data, support, confidence, ms).to_excel(outputfile)  # 保存结果

• 4、结果如下：
  
  
  从上面的关联规则来看，就可以针对某些商品采取相应的促销或商品摆放调整等措施。

4、时序模式

该模块我在另一篇博客中有详细的阐述。详见：《统计案例分析之预测社会消费品零售总额》。

5、离群点检测

就餐饮企业而言，经常会碰到如下问题。
1)如何根据客户的消费记录检测是否为异常刷卡消费?
2)如何检测是否有异常订单?
这一类异常问题可以通过离群点检测来解决。
离群点检测是数据挖掘中重要的一部分。

• 任务：发现与大部分其他对象显著不同的对象。大部分数据挖掘方法都将这种差异信息视为噪声而丢弃，然而在一些应用中， 罕见的数据可能蕴含着更大的研究价值。
• 应用范围：电信和信用卡的诈骗检测、贷款审批、电子商务、网络入侵和天气预报等领域。
• 成因：数据来源于不同的类，自然变异，数据测量和收集误差
• 类型：
  1、全局离群点和局部离群点：从整体来看某些对象没有离群特征，但是从局部来看，却显示了一定的离群性。
  2、数值型离群点和分类型离群点：以数据集的属性类型进行划分。
  3、一维离群点和多维离群点：一个对象可能有一个或多个属性。
• 检测方法：
  1、基于统计：构建一个概率分布模型，并计算对象符合该模型的概率，把具有低概率的对象视为离群点。前提是必须知道数据集服从什么分布，对于高维数据，检验效果可能较差。
  2、基于近邻度：在数据对象之间定义邻近性度量，把远离大部分点的对象视为离群点。该方法比较简单，低维数据可画散点图观察，不适用于大数据集，对参数的选择较为敏感。
  3、基于密度：数据集可能存在不同密度区域，离群点是在低密度区域中的对象，一个对象的离群点得分是该对象周围密度的逆。该方法给出了对象是离群点的定量度量，对不同区域的数据都能很好的处理；不适用于大数据集，参数选择较为困难。
  4、基于聚类：丢弃远离其他簇的小簇；或者先聚类所有对象，然后评估对象属于簇的程度。

下面主要介绍基于聚类方法的离群点检测的应用。

5.1 基于聚类的离群点检测方法

（1）丢弃远离其他簇的小簇：该过程可以简化为丢弃小于某个阈值的所有簇
（2）基于原型的聚类：首先聚类所有对象，然后评估对象属于簇的程度。可以用对象到他的簇中心的距离来度量属于簇的程度。

• 基于原型的聚类主要有两种方法评估对象属于簇的程度：一是度量对象到簇原型的距离，并用它作为该对象的离群点得分；二是考虑到簇具有不同的密度，可以度量簇到原型的相对距离，相对距离是点到质心的距离与簇中所有点到质心的距离的中位数之比。
• 诊断步骤：
  ①进行聚类：K-means算法，将样本聚为K类，并找到各类的质心。
  ②计算各对象到它的最近质心的距离。
  ③计算各对象到它的最近质心的相对距离。
  ④与给定的阈值作比较。

选择之前所提到的消费数据，找出数据中含有的离群点。具体代码示例如下：

# -*- coding: utf-8 -*-

import numpy as np
import pandas as pd

# 参数初始化
inputfile = '../data/consumption_data.xls'  # 销量及其他属性数据
k = 3  # 聚类的类别
threshold = 2  # 离散点阈值
iteration = 500  # 聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id')  # 读取数据
data_zs = 1.0*(data - data.mean())/data.std()  # 数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration)  # 分为k类，并发数4
model.fit(data_zs)  # 开始聚类

# 标准化数据及其类别
r = pd.concat([data_zs, pd.Series(model.labels_, index = data.index)], axis = 1)   # 每个样本对应的类别
r.columns = list(data.columns) + ['聚类类别']  # 重命名表头

norm = []
for i in range(k):  # 逐一处理
  norm_tmp = r[['R', 'F', 'M']][r['聚类类别'] == i]-model.cluster_centers_[i]
  norm_tmp = norm_tmp.apply(np.linalg.norm, axis = 1)  # 求出绝对距离
  norm.append(norm_tmp/norm_tmp.median())  # 求相对距离并添加

norm = pd.concat(norm)  # 合并

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
norm[norm <= threshold].plot(style = 'go')  # 正常点

discrete_points = norm[norm > threshold]  # 离群点
discrete_points.plot(style = 'ro')

for i in range(len(discrete_points)):  # 离群点做标记
  id = discrete_points.index[i]
  n = discrete_points.iloc[i]
  plt.annotate('(%s, %0.2f)'%(id, n), xy = (id, n), xytext = (id, n))

plt.xlabel('编号')
plt.ylabel('相对距离')
plt.show()

结果如下：

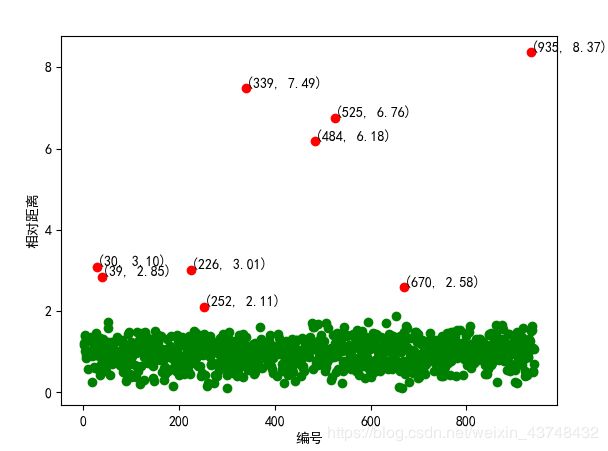
离散点检测距离误差图
从上图可以看出，该数据中8个红点表示有8个离群点。在之后的聚类中应将这些数据予以剔除。操作之后，聚类结果如下所示：

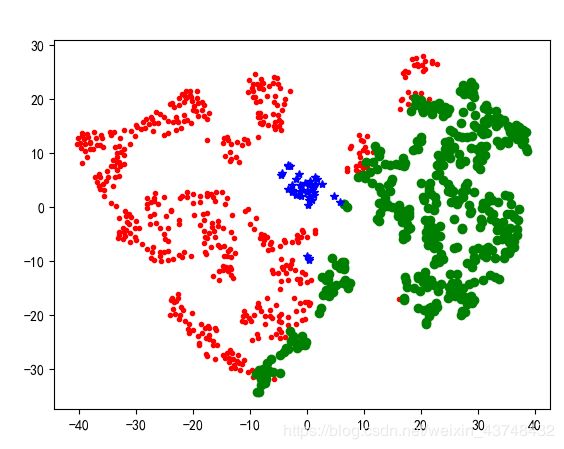
从上图来看，聚类效果仍然不是特别理想，需要对数据作进一步处理。