参数估计（点估计和区间估计）

“参数估计是以抽样分布为中介，用样本的参数特征对总体的参数进行数值估计的过程。”

一、点估计
1.点估计就是用样本统计量来估计总体参数。
概念理解：当我们想知道某一总体的某个指标的情况时，测量整体该指标的数值 的工作量太大，或者不符合实际，这时我们可以采用抽样的方法选取一部分样本测量出他们数值，然后用样本统计量的值来估计总体的情况。
例如：想了解一个学校学生的身高情况，就可以随机抽取一部分学生测量他们的身高，得到一个平均值，再用这个样本的均值去估计整体学生的身高情况，就是点估计。

常用的点估计有：用样本均值估计总体均值，用样本方差估计总体方差，用样本的分位数估计总体分位数，用样本的中位数估计总体的中位数。

2.点估计方法
矩估计法、顺序统计量法、最大似然法、
最小二乘法（对于点估计方法，放在另一篇文章中详细介绍）

3.由于用样本推断总体的过程一定存在估计误差，而点估计的估计误差无法衡量，所以点估计主要用于为定性研究提供数据参考，或者在对于总体参数估计精度要求不高时使用。

二、区间估计
1.区间估计就是在点估计的基础上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。
另外一种说法，区间估计是从点估计值和抽样标准误差出发，按给定的概率值建立包含待估参数的区间，这个给定的概率值称为置信度或置信水平，这个建立起来的包含待估计参数的区间称为置信区间。

2.关于置信水平（置信度）、置信区间和显著性水平：
置信区间是根据样本信息推导出来的可能包含总体参数的数值区间，置信水平表示置信区间的可信度；例如某学校学生的平均身高的区间估计：有95%的置信水平可以认为该校学生的平均身高为1.4米到1.5米之间，（1.4,1.5）为置信区间，95%是置信水平，即有95%的信心认为这个区间包含该校学生的平均身高。
置信水平用百分数表示，表示成（1-a）100%；a指的是显著性水平，表示总体参数不落在置信区间的可能性。

3.关于置信区间的计算：
通过部分样本来计算总体参数的一个置信区间有以下步骤：
a.明确要解决的问题，要估计的指标或参数是什么，
b.求抽样样本的平均值和标准误差，
注意区分标准差和标准误差:标准差反映的是整个样本对样本平均数的离散程度，标准差等于方差开根号；标准误差反映的是样本平均数对总体平均数的变异程度，标准误差等于样本标准差除n的开根号。
c.确定需要的置信水平，
d.查询z表，得到z值，
e. 计算置信区间，[a,b],a=样本均值-z标准误差，b=样本均值+z标准误差。

区间估计分为一个总体参数的估计和两个总体参数的估计

4.一个总体参数的区间估计：总体均值的区间估计，总体方差的区间估计，总体比例的区间估计；

4.1总体均值的区间估计：
均值抽样分布即样本均值组成的抽样分布，总体参数的估计方法跟样本均值的抽样分布有关；
Z分布其实就是标准正态分布，如果样本均值组成的抽样分布服从正态分布，那么将该正态分布标准化后即可得到Z分布，
Z分布的适用条件有两种：一是总体服从正态分布且总体标准差已知；二是总体分布未知，但是样本容量大于或等于30；
T分布：对于服从正态分布的总体且总体标准差未知的情况下 ，T分布是非常适用的均值抽样分布类型；
切比雪夫不等式：对于非正态分布总体或总体分布未知并且小样本的情况下，只能用切比雪夫不等式来近似估计总体均值的置信区间。
截图来自《人人都会数据分析：从生活实例学统计》

4.2 总体方差的区间估计：
总体方差的区间估计要用到卡方分布，如果数据总体服从正态分布，从中抽取样本容量为n的样本，样本方差为s^2,那么包含样本方差的卡方统计量服从自由度为n-1的卡方分布。卡方统计量是由总体方差和样本方差的比值组成的统计量，用于总体方差的区间估计。
卡方统计量的计算公式：
$${\chi }_{\alpha }^2(n-1)=\frac{(n-1)s^2}{{\sigma }_z^2}$$
总体方差的双侧置信区间估计公式为：
$$\frac{(n-1)s^2}{{\chi }_{\frac{\alpha }{2}}^2(n-1)}\le {\sigma }_z^2\le \frac{(n-1)s^2}{{\chi }_1^2-\frac{\alpha }{2}(n-1)}$$
其中带有a/2的为下标；
如果是单侧置信区间的话，只需要取上面式子的前半部分或者后半部分，并将a/2改成a即可得到单侧置信区间。

4.3 总体比例的区间估计：
或者叫总体比率的区间估计，跟二项分布有关，二项分布的理论是：事件发生概率是p,进行n次实验，其中x次实验该事件发生，则发生次数的概率分布服从二项分布；均值、方差为np,npq。
若将发生的次数转换成比率（x/n），则比率的概率分布也服从二项分布。
二项分布的特性：当抽取的样本容量n很大，是大 样本，使得np和nq（q为事件不发生的概率，等于1-p）的值都大于 5， 此时二项分布将近似于正态分布。
由于事件发生比率x/n服从二项分布，所以如果比率的二项分布近似于正态分布，就可以得到不利的区间估计。

在事件发生概率p已知的情况下，总体比率$$\overline{p_z}$$在置信度为1-a时，总体比率的置信区间为：
$$\overline{p_y}\pm Z_{\frac{\alpha }{2}}\sqrt{\frac{p(1-p)}{n}}$$
其中，$$\overline{p_y}$$为样本比率，$$\overline{p_z}$$为总体比率，
当事件发生概率p未知，可用样本中事件发生的概率即样本比率代替。

5. 两个总体参数的区间估计：
两个总体均值之差的估计，两个总体方差比的区间估计
两个总体与多个总体参数的区间估计在实际生活中的应用不是很多，更常用的是两个总体和多个总体参数的假设检验。 区间估计虽不常用，但是其与假设检验的应用原理是想通的。

5.1 两个总体均值之差的区间估计：
可以将单个总体均值的抽样分布推广到两个总体均值差的抽样分布，然后利用两个总体均值差的抽样分布推导出两个总体均值差的置信区间公式。
方差齐性/方差不齐：对于配对样本来说其方差可被认为是想等的，即方差齐性。

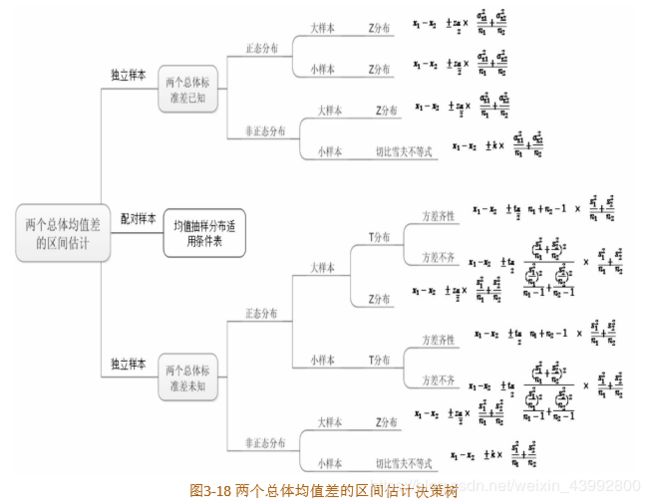
截图来自《人人都会数据分析：从生活实例学统计》

独立样本和配对样本：
独立样本：是指如果从一个总体中选取样本，抽样形式无论怎样改变都不会影响从另一个总体中抽取样本的概率，则这两个随机样本为独立样本；
配对样本：是指如果从一个总体中抽取样本的行为以某种方式决定了从另一个总体中抽取样本的概率，则这两个样本为成对样本或配对样本。

均值和方差的特点：
两个总体合并（相加或相减），那么合并后的总体均值等于原来两个总体的均值之和或均值之差；而合并后的总体方差都等于两个总体方差之和。

差值抽样分布可以看做单个总体的均值抽样分布，因此可套用“均值抽样分布适用条件表”，将公式修改一下即可：

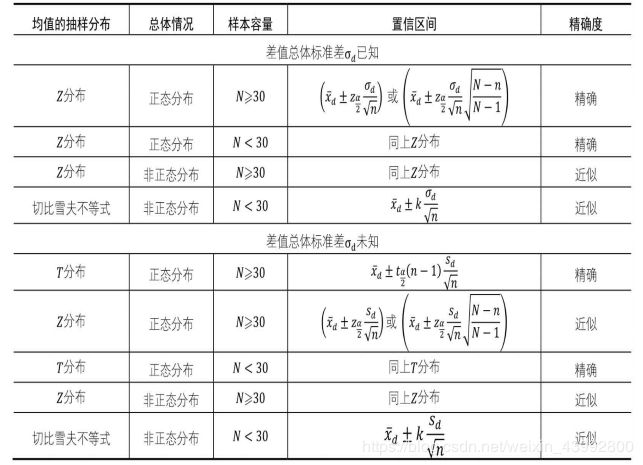
截图来自《人人都会数据分析：从生活实例学统计》

5.2 两个总体方差比的区间估计
F分布可用于求取两个正态分布总体方差比的置信区间。
F统计量可被看做是两个卡方统计量的商，F分布也被称为方差比分布。因为卡方分布要求总体服从正态分布，所以F分布也要求F统计量的两个总体都服从正态分布。
当给定置信水平时，可推出两个正态分布总体方差比的置信区间。

三、样本量的确定

1总体均值区间估计的样本量确定
在总体标准差已知的情况下，如果数据总体服从正态分布，则样本均值的抽样分布适用Z分布，就可以利用总体均值的置信区间公式来计算样本容量，总体均值的置信区间为：
$$\bar{x}\pm Z_{\frac{\alpha }{2}}\frac{\sigma }{\sqrt{n}}$$ 或 $$\bar{x}\pm Z_{\frac{\alpha }{2}}\frac{\sigma }{\sqrt{n}}\sqrt{\frac{N-n}{N-1}}$$

则总体均值的区间估计误差为：
$$\Delta \mu =Z_{\frac{\alpha }{2}}\frac{\sigma }{\sqrt{n}}$$
进而可以求得样本容量的公式：
$$n=(\frac{Z_{\frac{\alpha }{2}}\sigma }{\Delta \mu }{)}^2$$

以上是总体标准差已知时，当总体标准差未知时，一是可以用样本标准差代替，但是前提条件是样本容量要大于等于30；二是可以用过去试点调查的样本标准差代替；三是，如果知道总体数据中的最大和最小值，可用四分之一的最大与最小值的差值来代替总体标准差。

2.总体方差区间估计的样本量确定
总体方差的区间估计适用的抽样分布为卡方分布。卡方统计量为:
$${\chi }^2=\frac{(n-1)s^2}{{\sigma }^2}$$
由卡方分布的性质可知，当样本量足够大时，卡方分布近似于正态分布。卡方分布的均值为自由度（n-1）,卡方分布的方差为两倍的自由度2（n-1），那么在大样本的情况下，总体方差的置信区间为：
$$s^2=\pm Z_{\frac{\alpha }{2}}{s}^2\sqrt{\frac{2}{n}}$$
则总体方差的估计精度为：
$$\Delta {\sigma }^2=Z_{\frac{\alpha }{2}}{s}^2\sqrt{\frac{2}{n}}$$
由此可得到样本容量公式为：
$$n=\frac{\sqrt{2}{Z}_{\frac{\alpha }{2}}{s}^2}{\Delta {\sigma }^2}$$

3.总体比率区间估计的样本量确定
在确定总体比率的区间估计时，利用的是二项分布近似于正态分布的性质，即当抽取的样本量n很大时,是大样本，使得np>5且nq>5(p是事件发生的概率，q是事件不发生的概率，q=1-p)时，二项分布近似于正态分布。
总体比率的置信区间为：
$$\overline{p_y}\pm Z_{\frac{\alpha }{2}}\sqrt{\frac{p(1-p)}{n}}$$
则总体比率的估计误差为：
$$\Delta \overline{p_z}=Z_{\frac{\alpha }{2}}\sqrt{\frac{p(1-p)}{n}}$$
由此可得到样本容量为：
$$n=\frac{Z_{\frac{\alpha }{2}}^{2}p(1-p)}{\Delta {\overline{p_z}}^2}$$

注：本文主要参考《人人都会数据分析：从生活实例学统计》