已知聚类数目k的K-means算法及Matlab实现

1、k-means算法

首先，我们先来认识一个概念：聚类

“科普中国”科学百科词条对聚类的解释：将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类
而k-means算法就是在同一张图中将不同的簇识别出。

k-means算法过程：
1、生成k个随机点作为初始中心点（即簇的质心），k为用户指定的参数，故k为已知值
2、计算图中所有的点分别到k个质心的距离，将每个点分到离其最近的质心所在的簇中
3、根据每个簇中包含的所有点，重新计算该簇的质心
4、重复步骤2、3，直至各个质心不再发生改变时结束

2、Matlab实现

该实现过程建立于已知簇为2的情况下，即k=2。

在步骤1之前，我们利用matlab中的rand()函数生成随机样本：

%产生一个0至10之间的随机矩阵，大小为1*200；
X1 = rand(1,200)*10;
Y1 = rand(1,200)*10;
%产生一个5至15之间的随机矩阵，大小为1*200；
X2 = rand(1,200)*5+10;
Y2 = rand(1,200)*5+10;
%将横坐标、纵坐标分别合并
X = [X1;X2];
X = X(:);
Y = [Y1;Y2];
Y = Y(:);
%画出该初始的散点图
figure(1);
plot(X,Y,'.');
title('初始图');
box off;

此时，可得到x和y都分布在[0,15]范围内的随机样本，如下：

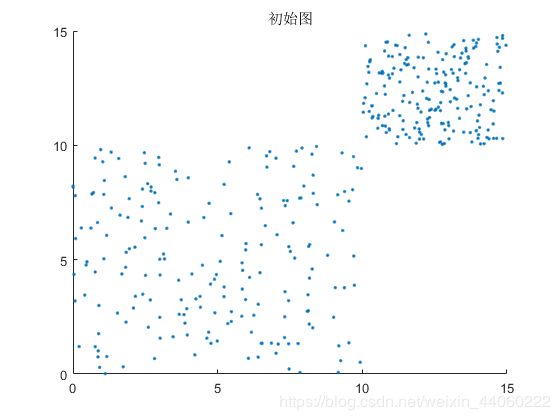
有了随机样本便可进入步骤1：

%假设已知k=2，步骤一：
%生成随机中心点：
x1 = rand(1,1)*15;
y1 = rand(1,1)*15;
x2 = rand(1,1)*15;
y2 = rand(1,1)*15;
%画出过程图
figure(2);
title('过程图');
plot(X1,Y1,'.',X2,Y2,'.',x1,y1,'*',x2,y2,'*');
box off;
%清除数组：
X1 = [];
Y1 = [];
X2 = [];
Y2 = [];

由于随机样本的范围，在步骤1中，我们随机生成的两个质心(x1,y1)、(x2,y2)，也将其横坐标和纵坐标限制于[0,15]范围内。
将数组X1、Y1、X2、Y2置为空数组，是为了下面的步骤中可循环使用。

此图中的随机点颜色不一致并不代表已分好簇，而是由于上一步生成的随机样本除了存储于X、Y中，还存储于X1、Y1、X2、Y2中.。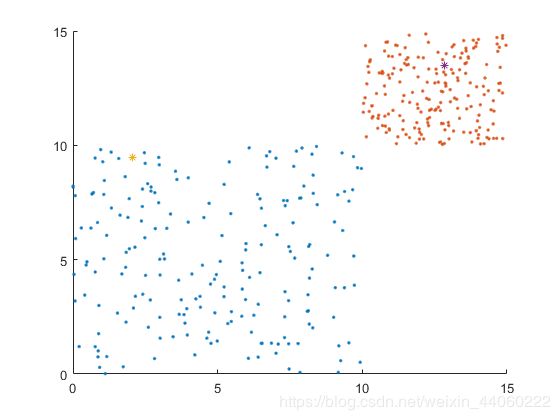
有了质心，便可粗略分簇，开始进入步骤3和步骤4：

%步骤三：重新计算中心点
x3 = mean(X1);
y3 = mean(Y1);
x4 = mean(X2);
y4 = mean(Y2);
count = 3;
%若跟原来的中心点不相同，则循环计算
while(~(x3==x1&&y3==y1&&x4==x2&&y4==y2)||(x3==x2&&y3==y2&&x4==x1&&y4==y1))
    %画出过程图
    figure(count);
    count=count+1;
    title('过程图');
    plot(X1,Y1,'.',X2,Y2,'.',x3,y3,'*',x4,y4,'*');
    box off;
    x1 = x3;
    y1 = y3;
    x2 = x4;
    y2 = y4;
    %清除数组：
    X1 = [];
    Y1 = [];
    X2 = [];
    Y2 = [];
    %步骤二：
    for i = 1:1:400
       if ((power((x1-X(i)),2)+power((y1-Y(i)),2))<(power((x2-X(i)),2)+power((y2-Y(i)),2))) 
           X1 = [X1,X(i)];
           Y1 = [Y1,Y(i)];
       else
           X2 = [X2,X(i)];
           Y2 = [Y2,Y(i)];
       end 
    end
    %重新计算中心点
    x3 = mean(X1);
    y3 = mean(Y1);
    x4 = mean(X2);
    y4 = mean(Y2);
end
%退出循环，则说明已找到合适的中心点
figure(count);
plot(X1,Y1,'.',X2,Y2,'.',x1,y1,'*',x2,y2,'*');
title('结果图');
box off;

函数mean()可用于计算数组的平均值。于是，在分别得到两个簇的所有随机点后，重新计算两个质心可使用mean()函数。
两点(x1,y1)、(x,y)间的距离d=sqrt((x-x1)²+（y-y1)²)，由于只需要比较大小，并不需要得出具体的值，因此在比较时忽略开根号，对结果并无影响。

从此图开始，颜色不同的随机点，分属两个簇。根据上图及下面两张图，可看出两个簇的质心的变化过程及随机样本在不同质心的情况下所属簇的情况。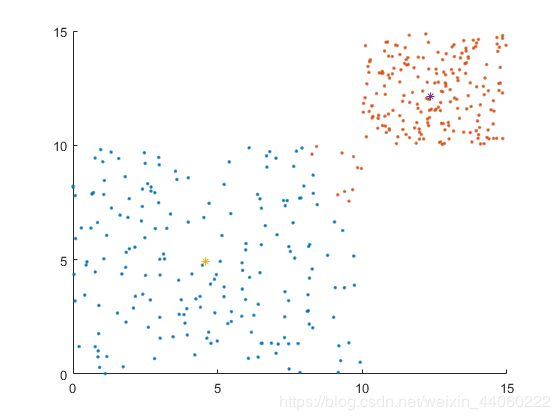

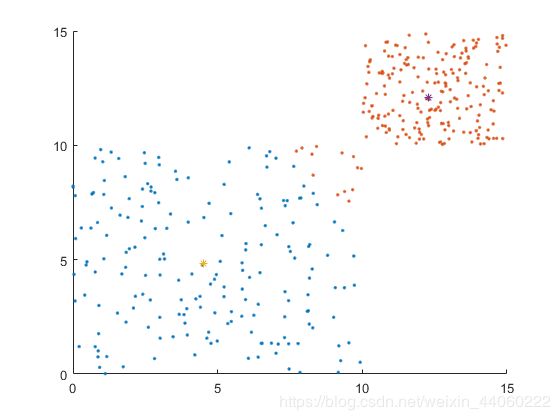
程序运行结束时，便可得到如下图所示的结果，该图与上步骤所得最后一幅图一样：

3、注意

1、k-means算法的簇值可分为两种情况：

• 只提供随机样本，簇为未知量，要求分簇。
• 提供随机样本及簇值，要求分簇。

以上讨论的为后者且明确簇为2，有较大的局限性。