数据处理（一）：python二维插值运算

0 前言

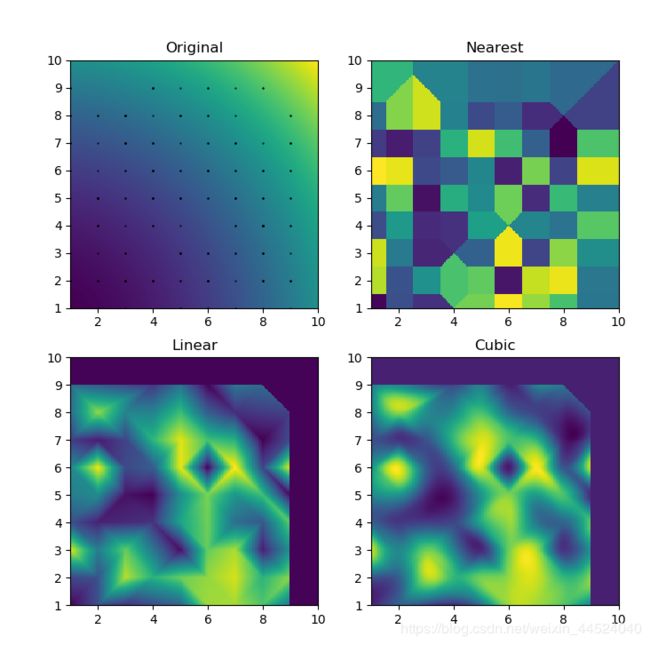
结果展示：黑色的点是前期输入生成的，彩色是后期生成的，代表不同像素点的数值

1 代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d #引入scipy中的一维插值库
from scipy.interpolate import griddata#引入scipy中的二维插值库

x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x, y)
f2 = interp1d(x, y, kind='cubic')

xnew = np.linspace(0, 10, num=41, endpoint=True)

plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic'], loc='best')
plt.show()
'''''
def func(x, y):
    return x**2+y**2
'''''
grid_x, grid_y = np.mgrid[1:10:200j, 1:10:500j]
#x方向在0-1上均匀生成200个数，y方向在0-1上均匀生成500个数

points = np.random.randint(1,10,(200, 2))
#随机生成（200，2）的矩阵，即200个点坐标

values = np.arange(0,200)#func(points[:,0], points[:,1])
#规定坐标值的值


grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
print(grid_z0[0][1])
#由于griddata返回的值是nddarry的格式的，所以可以读取他的数据，这里就是读取第[0][1]个数值的数

grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear',fill_value=5)
print(grid_z1[0][1])

grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic',fill_value=5)
print(grid_z1[0][1])
'''
plt.subplot(221)
plt.imshow(func(grid_x, grid_y).T, extent=(1,10,1,10), origin='lower')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)

plt.title('Original')
'''
plt.subplot(222)
plt.imshow(grid_z0.T, extent=(1,10,1,10), origin='lower')

plt.title('Nearest')
plt.subplot(223)
plt.imshow(grid_z1.T, extent=(1,10,1,10), origin='lower')

plt.title('Linear')
plt.subplot(224)
plt.imshow(grid_z2.T, extent=(1,10,1,10), origin='lower')

plt.title('Cubic')
plt.gcf().set_size_inches(8, 8)
plt.show()

2 解释

python中：
scipy.interpolate.griddata（points，values，xi，method =‘linear’，fill_value = nan，rescale = False ）

参数：
points：数据点坐标。可以是形状（n，D）的数组，也可以是ndim数组的元组。（已知点）

values：浮点或复数的ndarray，形状（n，）的数据值。（已知点对应的值）

xi ： 浮点数的二维数组或一维数组的元组，形状（M，D）插值数据的点。（被划分后的网格）

method：‘linear’，‘nearest’，‘cubic’，可选其中的插值方法之一。（插值方式）
{
nearest 返回最接近插值点的数据点的值。
linear 将输入点设置为n维单纯形，并在每个单形上线性插值。
cubic （1-d） 返回由三次样条确定的值。
cubic （2-d） 返回由分段立方，连续可微（C1）和近似曲率最小化多项式表面确定的值。
}

fill_value ： float，可选。用于填充输入点凸包外部的请求点的值。如果未提供，则默认为nan。此选项对“最近”方法无效。

rescale ： bool，可选。在执行插值之前，重新缩放指向单位立方体。如果某些输入维度具有不可比较的单位并且相差很多个数量级，则这非常有用。

返回值：nddarry 内插值数组

3 优化（未完待续）

import numpy as np
import matplotlib.pyplot as plt
#from scipy.interpolate import interp1d #引入scipy中的一维插值库
from scipy.interpolate import griddata#引入scipy中的二维插值库

four_boundary_point_original = np.array([[1,0],
                                [10,2],
                                [0,5],
                                [9,10]])
four_boundary_point_x = four_boundary_point_original.min(axis=0)
four_boundary_point_y = four_boundary_point_original.max(axis=0)
four_boundary_point = np.concatenate([four_boundary_point_x,four_boundary_point_y])
print(four_boundary_point)

'''
for i in range(4):
    input_x = float(input('please input 4 number:'))
    four_boundary_point.append(input_x)
'''
#four_boundary_point = [0,10,0,10]

mesh_size_x = round((four_boundary_point[2] - four_boundary_point[0])/0.05)
mesh_size_y = round((four_boundary_point[3] - four_boundary_point[1])/0.05)
print(mesh_size_y,mesh_size_x)
#将小格子的x方向分为步长为0.05的长度

def func(x, y):
    return x**2+y**2

x = np.linspace(four_boundary_point[0],four_boundary_point[2],mesh_size_x)
y = np.linspace(four_boundary_point[1],four_boundary_point[3],mesh_size_y)
grid_x, grid_y = np.meshgrid(x,y)
#x方向在0-1上均匀生成200个数，y方向在0-1上均匀生成mesh_size个数字

points = 10 * np.random.random((200,2))
#随机生成（200，2）的矩阵，即200个点坐标

values = np.arange(0,200)
#规定坐标值的值

grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
#print(grid_z0)
grid_z0[grid_z0<80]=0

grid_z0[(grid_z0>=80)&(grid_z0<160)]=50
grid_z0[(grid_z0>=160)&(grid_z0<=200)]=100
#由于griddata返回的值是nddarry的格式的，所以可以读取他的数据，这里就是读取第[0][1]个数值的数

grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear',fill_value=5)

grid_z1[grid_z1<80] = 1
grid_z1[(grid_z1>=80)&(grid_z1<160)] = 50
grid_z1[(grid_z1>=160)&(grid_z1<=200)] = 100

grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic',fill_value=5)


grid_z2[grid_z2<80] = 1
grid_z2[(grid_z2>=80)&(grid_z2<160)] = 50
grid_z2[(grid_z2>=160)&(grid_z2<=200)] = 100

plt.subplot(221)
plt.imshow(grid_z0.T, extent=(0,10,0,10), origin='lower')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)
plt.title('Nearest')

plt.subplot(222)
plt.imshow(grid_z1.T, extent=(0,10,0,10), origin='lower')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)
plt.title('Linear')

plt.subplot(223)
plt.imshow(grid_z2.T, extent=(0,10,0,10), origin='lower')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)
plt.title('Cubic')

plt.gcf().set_size_inches(8, 8)
plt.show()

#输入坐标点得到值
while True:
    point_wanted = []#[5.8，7.2]
    for i in range(2):
        point_wanted_input = float(input('please input the point you want'))
        point_wanted.append(point_wanted_input)

    point_wanted_x = int(round((point_wanted[0] - four_boundary_point[0])
                               /((four_boundary_point[2]-four_boundary_point[0])/mesh_size_x)))
    point_wanted_y = int(round((point_wanted[1] - four_boundary_point[1])
                               /((four_boundary_point[3]-four_boundary_point[1])/mesh_size_y)))
    #将输入的点进行四舍五入得到对应的array数组的值，（x点坐标-x左边界）/（（x左边界-x右边界）/分成的小格子）
    print(point_wanted_x,point_wanted_y)
    print(grid_z1[point_wanted_x][point_wanted_y])