牛客网剑指offer知识点归纳
牛客网剑指offer知识点归纳
第2题:replace()方法
str.replace(old, new[, max])
实例:
str = "this is string example....wow!!! this is really string";
print str.replace("is", "was");
print str.replace("is", "was", 3);
结果:
thwas was string example....wow!!! thwas was really string
thwas was string example....wow!!! thwas is really string
第3题:链表
链表并不等同于列表,元祖等,它们的区别在于链表中的每个元素都是由两部分组成,一部分是值(元素值),一部分是下一个元素的地址,输入一个链表,通常是已经指向第一个节点(每次使用完一个节点,则将指针指向第二个节点),保存在列表中。
题目描述:输入一个链表,按链表从尾到头的顺序返回一个ArrayList。
代码:
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
# 返回从尾部到头部的列表值序列,例如[1,2,3]
def printListFromTailToHead(self, listNode):
# write code here
res = []
while listNode:
res.append(listNode.val)
listNode = listNode.next
return res[::-1]
第3题:数组操作
a[i:j]:i指起始位置,默认为0;j是终止位置,默认为len(a),在取出数组中的值时就会从数组下标i(包括)一直取到下标j(不包括j)
a[i:j:h]:这里的i,j还是起始位置和终止位置,h是步长,默认为1。
若i/j位置上出现负数依然倒数第i/j个下标的位置,h若为负数则是逆序输出,这时要求起始位置下标大于终止位置;
在两个冒号的情况下若h为正数,则i默认为0,j默认为len(a);
若h为负数,则i默认为-1(即最后一个位置),j默认为-len(a)-1(下标0的前一个位置,这样就能输出到下标0了)
例:
1、
a='python'
b=a[1:4:]
print(b)
输出:yth #冒号后没有写明故代表默认步长为1
2、
a='python'
b=a[:-1]
print(b)
输出:pytho #-1代表倒数第一个位置,因为:前面的初始位置没有指定,默认为0,就从下标0一直取到最后一个位置之前
3、
a='python'
c=a[1:-2]
print(c)
输出:yth #-2代表倒数第二个位置,即从下标1取到倒数第二个位置之前
4、
a='python'
b=a[::-1]
print(b)
输出:nohtyp #前两个冒号和上面一致,就是确定起始位置和终止位置
#第三个参数-1是指步长为-1,也就是逆序输出
#这里a[::-1]相当于 a[-1:-len(a)-1:-1],也就是从最后一个元素到第一个元素
#所以[::-1]经常用来对一个数组进行逆序输出
5、
a='python'
b=a[-2:-7:-2]
print(b)
输出:otp #这里起始位置是-2,终点是-7(不包括,所以输出到-6位置),步长为-2
第4题 重建二叉树
二叉树知识点:
前序遍历:
若二叉树为空则结束返回,否则:
(1)访问根结点。
(2)前序遍历左子树。
(3)前序遍历右子树 。
中序遍历:
若二叉树为空则结束返回,否则:
(1)中序遍历左子树
(2)访问根结点
(3)中序遍历右子树
后序遍历:
若二叉树为空则结束返回,否则:
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根结点
关键点:
已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树;
已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树;
但是已知前序遍历序列和后序遍历序列,是不能确定一棵二叉树的。
该题目前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则二叉树为:
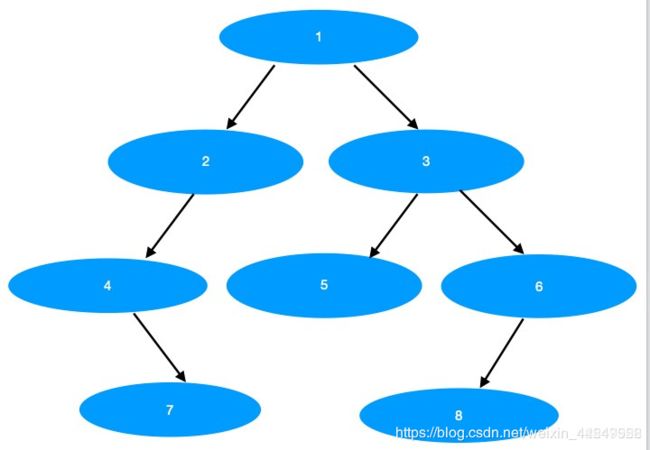
第5题 栈和队列
栈:先进后出
队列:先进先出
第6题 reverse()和reversed()方法区别
reverse():python中数组(列表)独有的方法,用于列表数据的反转
例:
list = [1, 3, 2, 4]
list.reverse()
print(list)
结果:[4,2,3,1]
reversed():python自带的方法,列表,元祖,字典的反转
例:
aa = (1, 2, 3)
print(tuple(reversed(aa)))
结果:(3,2,1)
第7题 斐波那契数列
斐波那契数列:在数学上,斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、34、……,被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
python表示n次方
2的2次方:22
2的3次方:23
2的n次方:2**n