统计自然语言处理——概率图模型(1)
概述
概率图模型(probabilistic graphical models)在概率模型的基础上,使用了基于图的方法来表示概率分布(或者概率密度、密度函数),是一种通用化的不确定性知识表示和处理方法。
根据图模型的边是否有向,概率图模型通常被划分成有向概率图模型和无向概率图模型。可将图模型粗略的表示为:
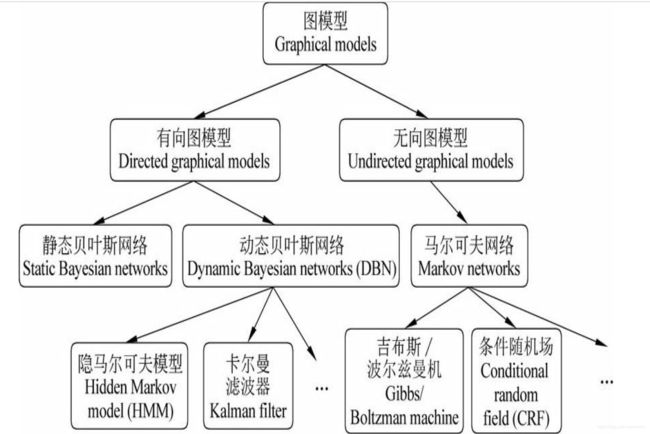
几种常见的图模型
- 动态贝叶斯网络(dynamic Bayesian networks, DBN)用于处理随时间变化的动态系统中的推断和预测问题;
- 隐马尔科夫模型(hidden Markov model,HMM)在语音识别,汉语自动分词和词性标注,统计机器翻译等若干语音语言处理任务中得到广泛应用;
- 卡尔曼滤波器则在信号处理领域有广泛的用途。
- 马尔科夫网络(Markov network)又称马尔科夫随机场(Markov random field,MRF),马尔科夫网络下的条件随机场(conditional random field,CRF)广泛应用于自然语言处理中的序列标注、特征选择、机器翻译等任务;
- 玻尔兹曼机(Boltzmann machine)近年来被用于依存句法分析和语义角色标注。
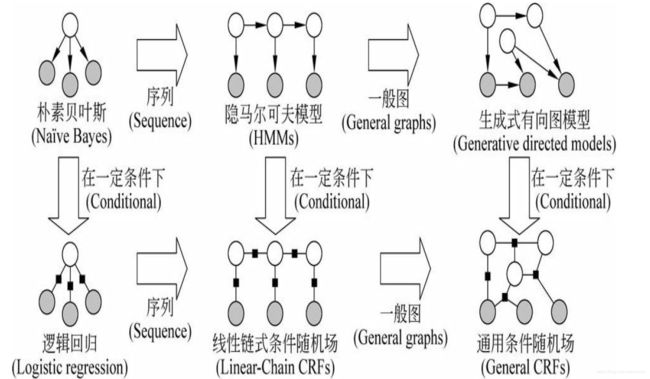
生成式模型与判别式模型
两者本质区别在于:生成式模型(产生式模型)假设y决定x,判别式模型(区分式模型)假设x决定y。
- 生成式模型:是所有变量的全概率模型,因此可以模拟(“生成”)所有变量的值。在这类模型中一般都有严格的独立性假设,特征是事先给定的,并且特征之间的关系直接体现在公式中。这类模型的嗯有点是处理单类问题时比较灵活,模型变量之间的关系比较清楚,模型可以通过增量学习获得,可用于数据不完整的情况。其弱点在于模型的推导和学习比较复杂。典型的生成式模型由:n元语法模型,HMM,朴素的贝叶斯分类器,概率上下文无关文法等。
- 判别式模型:符合传统的模型分类思想,认为y由x决定,直接对后验概率 p ( y ∣ x ) p(y|x) p(y∣x)进行建模,它从 x x x中提取特征,学习模型参数,使得条件概率符合一定形式的最优。在这类模型中特征可以任意给定,一般特征是通过函数表示的。这类模型的优点是:处理多类问题或分辨某一类与其他类之间的差异时比较灵活,模型简单,容易建立和学习。其弱点在于模型的描述能力有限,变量之间的关系不清楚,而且大多数区分式模型是有监督学习方法,不能扩展成无监督的学习方法。其代表的区分式模型有:最大熵模型,条件随机场,支持向量机,最大熵马尔科夫模型,感知机等。
贝叶斯网络
贝叶斯网络又称为信度网络或信念网络,是一种基于概率推理的数学模型,其理论基础是贝叶斯公式。
定义
贝叶斯网络就是一个有向无环图(DAG),结点表示随机变量,可以是客观测量、隐含变量、未知参量或假设等;结点之间的有向边表示条件依存关系,箭头指向的结点依存于箭头发出的结点(父节点)。两个结点没有链接关系表示两个随机变量能够在某些特定情况下条件独立,而两个结点有连接关系表示两个随机变量在任何条件下都不存在条件独立。条件独立是贝叶斯网络所依赖的一个核心概念。 每个节点都与一个概率函数相关,概率函数的输入是该节点的父节点所表示的随机变量的一组特定值,输出为当前节点表示的随机变量的概率值。概率函数值的大小实际上表达的是节点之间依存关系的强度。
【例】 如果一篇文章是关于南海岛屿的新闻(将这一事件记作“News”),文章可能包含介绍南海岛屿历史的内容(这一事件记作“History”),但一般不会有太多介绍旅游风光的内容(将事件“有介绍旅游风光的内容”记作“Sightseeing”)。我们可以构造一个简单的贝叶斯网络(其中“T”表示有,是,包含;“F”表示没有,不是,不包含)。
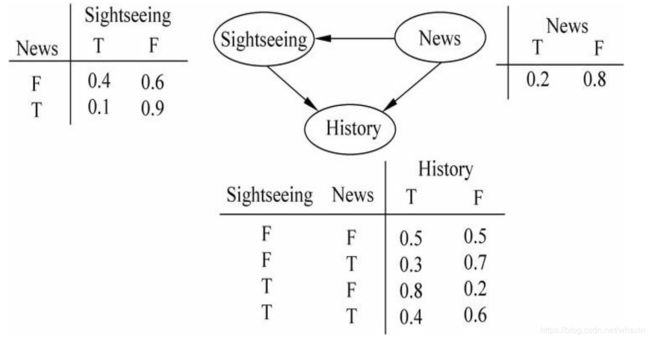
则三个事件的联合概率函数为:
P ( H , S , N ) = P ( H ∣ S , N ) × P ( S ∣ N ) × P ( N ) P(H,S,N) =P(H|S,N)\times P(S|N)\times P(N) P(H,S,N)=P(H∣S,N)×P(S∣N)×P(N)
这个模型可以回答如下类似的问题:如果一篇文章中含有南海岛屿历史相关的内容,该文章是关于南海新闻的可能性有多大?
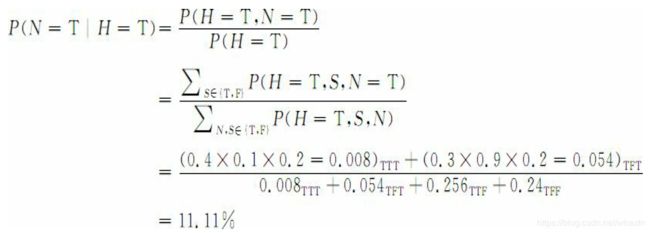
构造贝叶斯网络是一项复杂的任务,设计表示、推断和学习三个方面的问题:
- 表示:在某一随机变量的集合 x = { X 1 , L , X n } x=\{X_1,L,X_n\} x={X1,L,Xn}上给出其联合概率分布 P P P。这主要问题是,即使随机变量仅有两种取值的简单情况下,一个联合概率分布也需要对所有 2 n 2^n 2n种不同的取值下的概率情况进行说明,这无论从计算代价和人的认知上,都是不可能的或者是代价昂贵的。
- 推断:由于贝叶斯网络是变量及其关系的完整模型,因此可以回答关于变量的询问,如当观察到某些变量时,推断另一些变量子集的变化。在已知某些证据的情况下,计算变量的后验分布的过程称作概率推断。推理方法包括变量消除法,团树法等。近似推理算法有重要性抽样法,随机马尔科夫链蒙特卡罗模拟法,循环信念传播法和泛华信念传播法等。
- 学习:参数学习的目的是决定变量之间相互关联的量化关系,即依存强度估计。常用的参数学习方法包括最大似然估计法,最大后验概率法,期望最大化方法和贝叶斯估计方法。
马尔科夫模型
随机过程又称随机函数,是随时间而随机变化的过程。马尔科夫模型描述了一类重要的随机过程。我们常常需要考察一个随机变量序列,这些随机变量并不是相互独立的,每个随机变量的值依赖于这个序列前面的状态。
如果一个系统有 N N N个有限状态 S = { s 1 , s 2 , ⋯ , s N } S=\{s_1,s_2,\cdots,s_N\} S={s1,s2,⋯,sN},那么随着时间的推移,该系统将从某一状态转移到另一个状态。 Q = ( q 1 , q 2 , ⋯ , q T ) Q=(q_1,q_2,\cdots,q_T) Q=(q1,q2,⋯,qT)为一个随机变量序列,随机变量的取值为状态集 S S S中的某个状态,假定在时间 t t t的状态记为 q t q_t qt。对该系统的描述通常需要给出当前时刻 t t t的状态和其前面所有状态的关系:系统在时间 t t t处于状态 s j s_j sj的概率取决于其在时间 1 , 2 , ⋯ , t − 1 1,2,\cdots,t-1 1,2,⋯,t−1的状态,该概率为
P ( q t = s j ∣ q t − 1 = s i , q t − 2 = s k , ⋯ ) P(q_t=s_j|q_{t-1}=s_i,q_{t-2}=s_k,\cdots) P(qt=sj∣qt−1=si,qt−2=sk,⋯)
如果在特定条件下,系统在时间 t t t的状态只与其在时间 t − 1 t-1 t−1的状态相关,即
P ( q t = s j ∣ q t − 1 = s i , q t − 2 = s k , ⋯ ) = P ( q t = s j ∣ q t − 1 = s i ) P(q_t=s_j|q_{t-1}=s_i,q_{t-2}=s_k,\cdots)=P(q_t=s_j|q_{t-1}=s_i) P(qt=sj∣qt−1=si,qt−2=sk,⋯)=P(qt=sj∣qt−1=si)
则该系统构成一个离散的一阶马尔科夫链。
进一步,如果只考虑独立于时间 t t t的随机过程:
P ( q t = s j ∣ q t − 1 = s i ) = a i j , 1 ≤ i , j ≤ N P(q_t=s_j|q_{t-1}=s_i)=a_{ij},1\leq i,j\leq N P(qt=sj∣qt−1=si)=aij,1≤i,j≤N
该随机过程为马尔科夫模型。其中,状态转移概率 a i j a_{ij} aij必须满足一下条件:
a i j ≥ 0 , ∑ j = 1 N a i j = 1 a_{ij}\geq 0, \sum_{j=1}^Na_{ij}=1 aij≥0,j=1∑Naij=1
显然,有 N N N个状态的一阶马尔科夫过程有 N 2 N^2 N2次状态转移,其 N 2 N^2 N2个状态转移概率可以表示成一个状态转移矩阵。例如,一段文字中名词、动词、形容词三类词性出现的情况可由三个状态的马尔科夫模型描述:
状态 s 1 s_1 s1:名词
状态 s 2 s_2 s2:动词
状态 s 3 s_3 s3:形容词
假设状态之间的转移矩阵如下:

则 O = O= O=“名动形名”的概率为
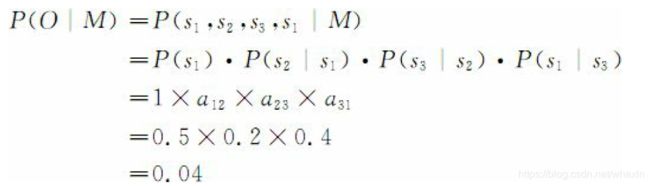
马尔科夫模型又可视为随机的有限状态机。如图所示:
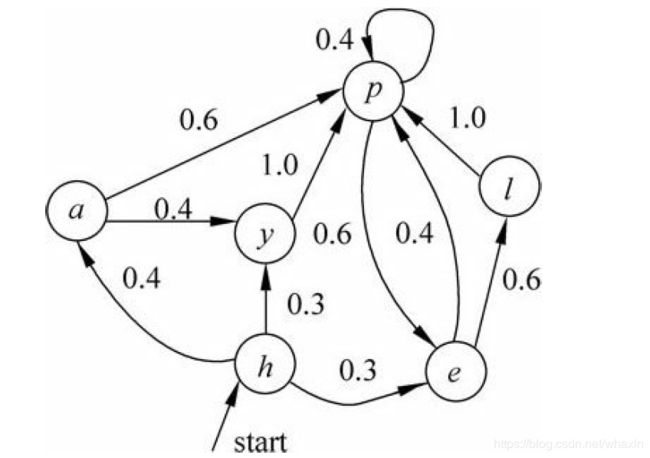
一个马尔科夫链的状态序列的概率可以通过计算形成该状态序列的所有状态之间转移弧上的概率乘积而得出,即
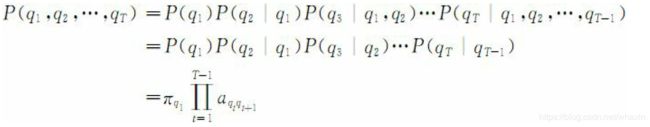
根据图中转移概率,我们可以得出:
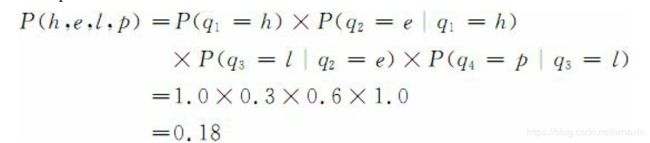
显然,n元语法模型,当 n = 2 n=2 n=2时,实际上就是一个马尔科夫模型。但是当 n ≥ 3 n\geq 3 n≥3时,就不是一个马尔科夫模型,因为它不符合马尔科夫模型的基本约束。不过 n ≥ 3 n\geq 3 n≥3的n元语法模型确定数量的历史来说,可以通过将状态空间描述成多重前面状态的交叉乘积的方式,将其转换成马尔科夫模型。在这种情况下,将其称为m阶马尔科夫模型,这里的m是用于预测下一个状态的前面状态的个数,那么,n元语法模型就是 n − 1 n-1 n−1阶马尔科夫模型。
总结
本文只是简单介绍了概率图模型中简单的贝叶斯网络和马尔科夫模型,作为学习概率图的基础。后面将持续介绍概率图后面进阶内容:隐马尔可夫模型,层次化的隐马尔可夫模型,马尔科夫网络,最大熵模型,最大熵马尔科夫模型,条件随机场等内容。