编译原理——词法分析

根据上课内容顺序写的博客，并不是按照书的目录来的
使用龙书以及编译程序设计原理（第二版）金成植、金英编著
老师的PPT是英文的，我自己随便翻的，不一定对

---

词法分析(scanning)

---

---

概述

    知识关系图
    
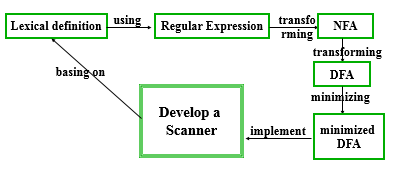
    开发一个词法分析器是在词法定义的基础上的，词法定义需要使用正则表达式
    正则表达式可以转换为NFA（Non-determinate finite automata 不确定的有穷自动机）
    NFA可以转换为DFA（determinate finite automata确定的有穷自动机）
    DFA可以极小化，进而使用为开发词法分析器的工具

    编译器中词法分析的地位
    
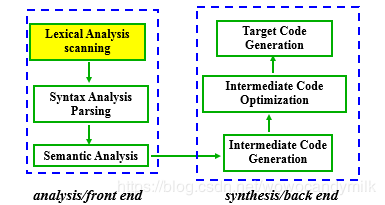
    词法分析是编译器中最底层的分析。构造词法分析器的前提是给出语言中单词结构的定义。
    不同语言的单词类别和结构不完全相同，因此不同语言的词法分析器也就不尽相同，但是其构造原理是类似的。
    构造方法可以分为人工方法和自动化方法两种。

词法分析器的基本功能

• 输入
  • 源程序
• 输出
  • 词法单元（token）序列
• 功能描述
  • 读取源程序
  • 根据源语言的词法定义依次识别单词
  • 构造单词的内部表示——词法单元
  • 检查词法错误
  • 返回词法单元序列

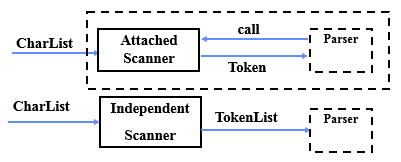
    词法分析器的两种形式

• 独立
  • 一个词法分析器是编译器中的独立的部分
  • 输出：词法单元的序列
• 关联
  • 作为语法分析器的一个附属机构
  • 当被语法分析器调用时返回一个词法单元
    

词法分析器的一些概念

词法单元

• 单词的内部表示是词法单元 token
• 是编程语言中最小的语法单元
• 词法单元的表示

词法单元的类别token-type	词法单元的内容（语义）semantic information

• token设计示例

程序表示	ASCII码	单词的类别	单词的内容（语义）
if	9666	01	9666
then	478656E6	02	478656E6
begin	26567696E6	03	26567696E6

• 一个词法单元包括两个部分
  • 词法单元的类别 token type token.class
  • 词法单元的内容（语义） attributes(semantic information) token.seman
• 例子

• token类别
  • 标识符 x, y1, ……
  • 常数 1,12,123,12.3
  • 以下的类别中，每一个示例都可以被看做一个种类
    • 关键字（保留字） int , real, main
    • 操作符 +，-，/，*，<,>,……
    • 分隔符 ;, {, } , ……
• token内容（语义）
  • 标识符 字符串（变量名、常量名、过程名、数组名等）
  • 常数 数值（整型常数、实型、布尔、字符常数）
  • 关键字（保留字） 关键字表里的数字(语言系统自身定义，通常是字母组成的字符串)
  • 操作符或分隔符 它自己

关键字

• 关键字
  • 有特殊意义的单词
  • 不能作为其他意义使用
• 保留字
  • 被语言系统自身定义的有特殊意义的单词
  • 能作为其他意义使用，需要重载之前的意思
• 关键字表
  • 用来记录所有的被源程序语言定义的关键字

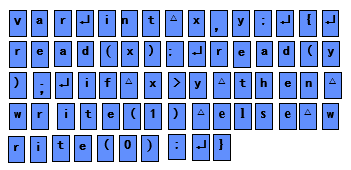
    例子分析

      
     源程序例子

    

     词法单元序列
    

空格，缩进，换行，注释

没有语义意义
只是为了可读性而存在
可以被移除
计算行号

词法的结尾

• 两种选择情况
  • 读取到了代表程序结尾的符号
    • 例如 PASCAL语言中是 ‘.’
  • 源程序文件的尾部

词法错误

• 在词法分析过程中可以发现有限类型的错误主要有两种
  • 非法字符 & ←
  • 第一个字符是错误的 “ /abc”
• 错误修正
  • 一旦一个词法错误被发现，词法分析器不会停止，会采取措施来继续词法分析的过程
  • 忽视字符流，开始读取下一个字符
  • if &a then x = 12.else …
  • 编译程序设计原理第二版书 P35 【错误修正】 【修正手段】

---

有穷自动机

确定有穷自动机DFA的定义和实现

DFA的定义

    DFA的正式定义
    一个DFA定义了一个字符串集合
    每个字符串是一个字符的序列，字符属于∑
    起始状态给出生成字符串的起始点
    终端状态给出了终点
    转换函数制定了生成字符串的规则

    确定有穷自动机包含以下五个部分，在一个符号集上可定义出很多不同的自动机。
    每个自动机都是某给定符号集上符号串的识别（接收）器。
    [1]符号集∑（输入符号集）
    [2]状态集合SS={S₀,S₁,S₂,S₃,…,S_n}
    [3]开始状态S₀
    [4]终止（接受）状态集 {S_i1,S_i2,…,S_in}
    [5]状态转换器

    

• DFA的特点
  • 一个开始状态
  • 对于一个状态和一个符号，最多只有一条边
• DFA的功能
  • 定义了一个字符串集合
  • 能被用来定义一个编程语言的词法结构

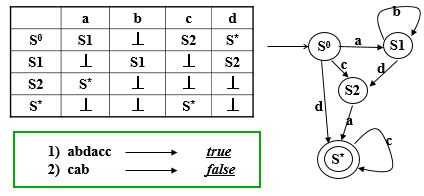
    两种表示方式

    表：易于实现
    图：易于阅读和理解

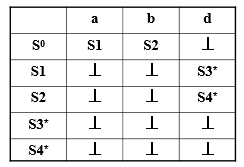
    转换表
    包括开始状态S₀，终止状态S*，行（字符），列（状态），单元（状态或⊥）
    

    转换图
    均用图形表示，包括开始状态，终止状态（同心圆），状态，边（箭头）
    下图是上述转换表对应的转换图
    

    一些概念

    DFA能接受的字符串

    假设A是一个DFA，a₁ a₂ a₃ … a_n是一个字符串
    如果存在一个状态序列(S₀,S₁,S₂,…,S_n)，满足以下
    
    其中S₀是开始符号，S_n是接收状态之一，字符串a₁ a₂ a₃ … a_n可被DFA A 所接受，表示为L(A)

    DFA定义的字符串集

    所有的字符串集中的字符串都是被DFA A所接受的被称为A定义的字符串集，

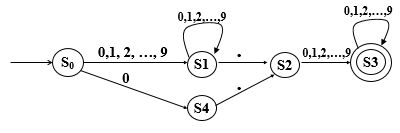
    无符号实数的DFA实例

    特殊实例

    自动机的画法，可以按照以下实例来画
    

DFA的实现

目标（实现DFA的意义）

• 给出一个定义了一个字符串集规则的DFA
• 开发一个程序
  • 读取字符串
  • 检查这个字符串是否能被DFA接受

如果一个字符串能被一个DFA接手

• 进入下一个状态
• 在终止状态结束

如果一个字符串不能被DFA接手

• 买有下一个状态（⊥）
• 不会在终止状态停止

两个方法开发DFA

• 状态转换表
• 状态转换图

    基于状态转换表的实现

    输入：一个字符串
    输出：被接受则是true，否则是false
    数据结构：转换表（二维数组T）
    两个变量：流状态CurrentState,流字符CurrentChar
    基本算法：

1. CurrentState = S₀
2. 读取流字符的第一个字母
3. 如果流字符不是字符串的最后一个
   如果T（CurrentState,CurrentChar）≠error
       CurrentState=T（CurrentState,CurrentChar）
       读取下一个字符串中的字符作为流字符
       goto 3;
4. 如果流字符是字符串的最后一个且流状态是终止状态的一个返回true，否则返回false

    实例：
    

    基于状态转换表实现的程序结构：
    

    基于状态转换图的实现

    每一个状态都对应一个case语句
    每一条边都对应一个goto语句
    对于接受状态，添加一个分支，如果流字符是字符串的最后一个则接受
        

            

    从S₀出发，如果遇到a的边，则goto LS₁,以此类推
    从S₁出发，如果遇到b的边，则goto LS₁,以此类推
    ……

    实例：
    

    

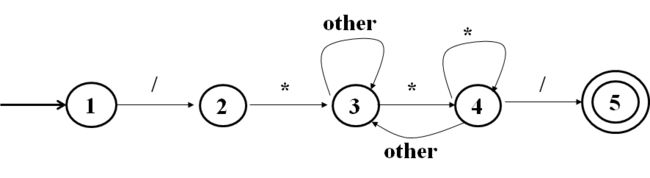
{ state 1 }
if the next character is "/" then
   advance the input; { state 2 }
   if the next character is "*" then
      advance the input;{ state 3 } 
      done: = false;
      while not done do 
       while the next input character is not "*" do
         advance the input;
       end while;
     advance the input; { state 4 }
     while the next input character is  "*" do
       advance the input;
     end while;
     
 if the next input character is "/" then
         done: = false;
      end if;
      advance the input;
    end while;
    accept; { state 5 }
    else{ other processing }
  end if;
  else { other processing }
end if;

state := 1;{ start }
while state = 1,2,3 or 4 do
 case state of
 1: case input character of
          "/" :  advance the input;  state := 2;
          else state := ...{ error or other };
     end case;
 2: case input character of
         "*" :  advance the input;  state :=3;
         else state := ...{ error or other };
    end case;
 3: case input character of
        "*" :  advance the input;  state := 4; 
        else advance the input { and stay in state 3 }
    end case;
 4: case input character of
         "/" :  advance the input;state := 5;
         "*" :  advance the input; { and stay in state 4 }
         else advance the input;state :=3;
     end case;
 end case;
end while;
if state = 5 then accept else error;

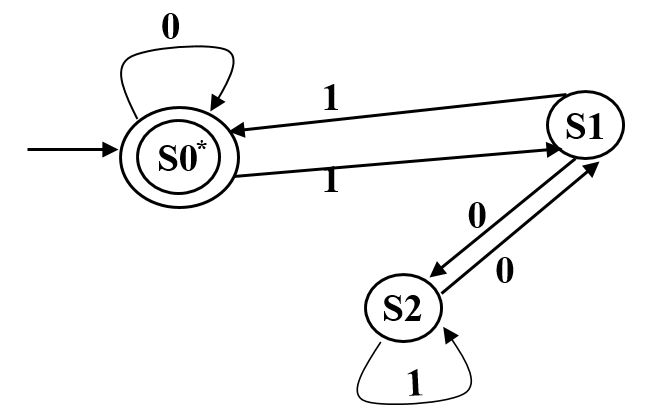
    实例：

    设二进制数i, 后面跟一个0，产生符号串2i, 后面跟一个1，产生符号串2i+1
    余数: i/3=q, 2i/3=2q

	2i	2i+1
q=0	0	1
q=1	2	0
q=2	1	2

    ∑ = {0,1}
    SS = { S₀, S₁, S₂},
    S_q represents the state that the remainder(余数) is q; (q=0,1,2)

    

不确定的有穷自动机NFA

NFA的定义

非确定有限状态自动机（Nondeterministic Finite Automata，NFA）由以下元素组成：

一个有限的状态集合S
一个输入符号集合Σ，并且架设空字符ε不属于∑
一个状态迁移函数，对于所给的每一个状态和每一个属于∑或{ε}的符号，输出迁移状态的集合。
一个S中的状态s₀作为开始状态（初始状态）
S的一个子集F，作为接受状态（结束状态）

与DFA的区别：

1. 一个状态的不同输出边可标有相同的符号
2. 允许有多个开始状态
3. 允许有ε边

	DFA	NFA
开始状态	一个开始状态	开始状态集合
ε	×	√
T(S,a)	S’ 或者 ⊥	{S1,S2,…Sn} 或者 ⊥
实现	容易	不确定性

NFA实例：

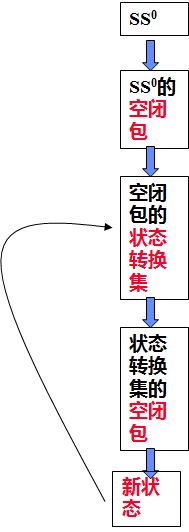
NFA到DFA的转换

解决两个问题

• ε边 ε闭包
• 用相同的符号合并这些边 NextStates(SS,a)

NFA到DFA的转换

• 使用一个NFA的状态集作为DFA的一个状态
• 确保接受相同的字符集合

计算ε闭包的过程

对于一个给定的NFA A，和一个状态集SS

• ε-closure(SS)=SS
• 如果存在一个属于状态集SS的状态S，状态S有一个ε边指向状态S’，且状态S’不输入ε闭包，添加S’进入ε闭包
• 重复这个过程直到没有一个状态有ε边能到达不在ε闭包里的状态

ε闭包——示例

转向状态

对于一个给定的状态集SS和一个符号a在NFA A中
转向状态NextStates(SS,a)={s|if there is a state s₁∈SS,并且一条边S₁→S（边为a）在A中}

算法

• 对于一个给定的NFA A={∑， SS, SS⁰, Φ, TS}
• 生成一个等价的DFA A’={∑， SS’, S⁰, Φ’, TS’}
• 步骤
  • S⁰=ε-closure(SS⁰), add SS⁰ to SS’
  • 从SS’中选择一个状态S，对于任意符号a∈Σ
    • 让S’=ε-closure(NextStates(S,a))
    • add(S,a) → S’ to Φ’
    • 如果 S’∉SS’ 添加状态S’到SS’
  • 重复上述步骤直到所有的状态都处理过（无新状态）
  • 对于一个状态S在SS’ S={S₁,…,S_n},如果存在S_i∈TS 则S是一个接受状态在A’中，添加S进TS’

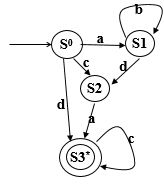
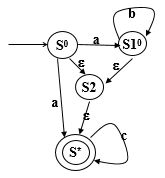
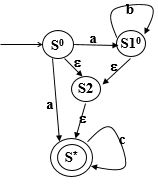
PPT例子

Σ={a,b,c}
S0=ε-closure({S⁰,S1⁰})={S⁰,S1⁰,S2,S*}

	a	b	c
{S0,S10,S2,S*}	{S10,S*,S2}	{S10,S*,S2}	{S*}
{S10,S*,S2}		{S10,S*,S2}	{S*}
{S*}			{S*}

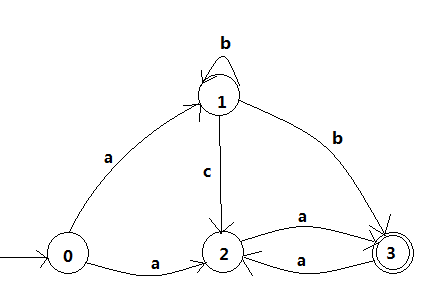
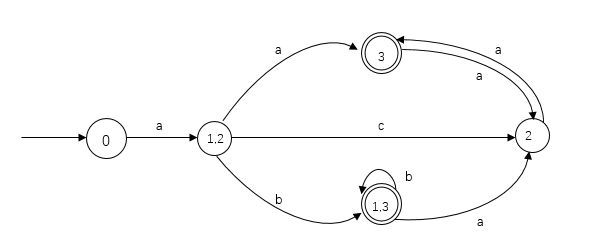
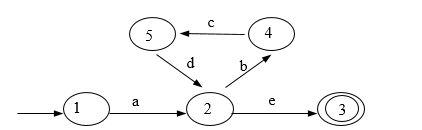
书上的例子

NFA:

因为3是NFA的接受状态号，所以DFA的接受状态是[3]和[1,3]，构造过程如下

转换后的DFA如下图

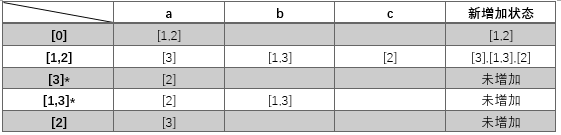
其他例子

（NFA的确定化）NFA转换为等价的DFA

NFA转DFA与DFA简化

子集构造法NFA转换成DFA

DFA的极小化

两个DFA的等价：两个DFA接受的字符串集相同
在这些接受相同字符串集的DFA中，极小化DFA是有最少的状态数的那个DFA

等价状态：对于两个状态S1和S2在同一个DFA中，如果将S1、S2作为开始状态并且他们接受相同的字符串集，S1和S2可以称作等价的状态

两种极小化DFA的方式：
状态合并（合并等价状态）
状态分离（分离不等价状态）

算法：

• DFA A = {Σ， SS, S⁰, Φ，TS}
• 生成一个等价DFA A’={Σ， SS’, S⁰’, Φ’，TS’}
• 分步骤
  • 两个群组 {非终点状态} {终点状态}
  • 选择一个状态SS_i集合 SS_i={Si1,…,Sin}, 用split(SS_i)替换SS_i
  • 重复上一步知道所有的群组都不能再分了
  • SS’=群组的集合
  • S^0’是由S⁰组成的群组
  • 如果群组是由A的终态组成的，它也是A’的终态
  • Φ’： SS_i→SS_j 边为a 如果A中有Si → Sj 边为a Si∈SS_i Sj∈SS_j

分离状态集

已知：
DFA A = {Σ， SS, S⁰, Φ，TS}
状态组 {SS1,…,SSm}, SS1∪…∪SSm=SS
SS_i={Si1,…,Sin}

split(SS_i)是把SS_i分成两个群组G1和G2的
for j=1 to n
    for any a∈Σ
    if (Si1, a) → Sk ^ (Sij, a) → S1 ^ Sk和S1属于同一个群组SSp
          添加Sij到G1
    否则，添加Sij到G2

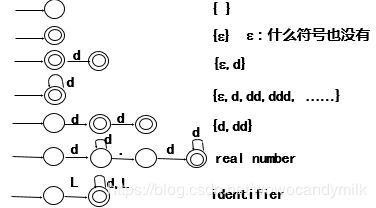
简单的例子

                    

---

正则表达式

正则表达式的定义

正则表达式Regular Expressions （RE）

名称	英语	解释
字母表	alphabet	一个符号的非空有限集合，写成Σ，其中的元素成为符号
符号串	string	有限的符号序列，使用 λ 或 ε 来表示空串
符号串长度	length ofstring	字符串中字符的数量，使用β的绝对值来表示字符串β的长度
符号串连接操作	concatenate operator for strings	两个字符串链接的操作αβ 通常有λβ=βλβ
符号串集的乘积	product of set of strings	两个字符串集的乘积操作 AB={αβ，α∈A，β∈B}
符号串集的方幂	power of set of strings	A0={λ} A1=A, A2=AA Ak=AA…A(k)
符号串集的正闭包	positive closure	A+=A1∪A2∪A3…
符号串集的星闭包	star closure	A*=A0∪A1∪A2∪A3…

{a,ab} {c,d,cd} ={ac,ad,acd,abc,abd,abcd}
{a,ab}⁺ = {a,ab}∪{a,ab}{a,ab}∪…
    = {a,ab,aa,aab,aba,abab,……}
{a,ab}* ={λ}∪{a,ab∪{a,ab}{a,ab}∪…
    = {λ,a,ab,aa,aab,aba,abab,……}

正则表达式的定义
  每个正则表达式定义一个正则集。若用RE表示Σ上的正则表达式，并用L(RE)表示RE所表示的正则集，则RE的语法定义和相应正则集如下面所述，其中A和B表示正则表达式，并且a表示字母表Σ中的任一符号。

1. ∅∈RE    L(∅)={ }
2. ε∈RE     L(ε)={ε}
3. a∈RE     L(a)={a}
4. (A)∈RE     L((A))=L(A)
5. A | B∈RE     L(A | B)=L(A)∪L(B)
6. A · B∈RE     L(A · B)=L(A)L(B)
7. A* ∈RE      L(A*)=L(A)*
   

正则表达式的性质

RE局限性

• RE不能定义结构比如
  • 配对 pairing
  • 嵌套 nesting
• RE不能描述那些包括有限重复数的结构（对称性字符串）
• 例如 WCW W是一个字符串包括a和b
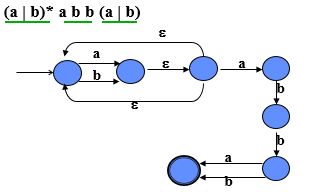
• (a|b)* c (a|b)* 不能被使用，因为它不能保证字符串在c的两边是总是相同

正则定义

正则定义：
使用RE来定义一个长字符串集是非常不方便的，因此介绍另一种形式的记法，成为形式化定义
形式化定义的主要目的是为RE中的一些子表达式命名
例如：
(1|2|…|9)(0|1|2|…|9)*
NZ_digit =1|2|…|9
digit = NZ_digit |0
NZ_digit digit*

定义C0的词法结构
字母letter = a|…|z|A|…|Z
数字digit = 0|…|9
自然数NZ-digit = 1|…|9
保留字Reserved words:
  Reserved = {| }| read| write
标识符Identifiers: =letter(letter|digit)*
常量Constant:
  integer: int = NZ-digit digit* | 0
其他符号Other symbols: syms = +|*| := | ;
词法结构Lexical structure:
  lex = Reserved | identifier |int | syms

从正则表达式到DFA的转换

PPT上例题

从正则表达式(RE)到最小确定性有限状态自动机(DFA)

正则表达式转DFA

词法分析：从RE（正则表达式）到DFA（确定的有限状态机）

正则表达式 ：龙书习题

编译原理习题

---

词法分析器的设计和实现

手动构造一个词法分析器
使用RE进行词法定义 ，转化为NFA， 转化为DFA， 极小化DFA， 实现即开发一个词法分析器

用DFA构造一个词法分析器

• 实现一个DFA
  • 只需要检查一个字符串能不能被DFA接受
• 实现一个词法分析器
  • 不检查
  • 但是要识别一个可接受的字符串（单词） 并且建立其内部表示

一些问题：

• 独立的DFA还是有联系的DFA（看上一篇博客的内容）
• 跳过那些特殊字符
  • 空白，缩进，注释，返回（行号）
• 什么时候停止词法分析
  • 在源文件的末尾
• 关键字和标识符
• 怎么知道识别一个词法单元的结束

立即接受状态和延迟接受状态

C0语言的DFA

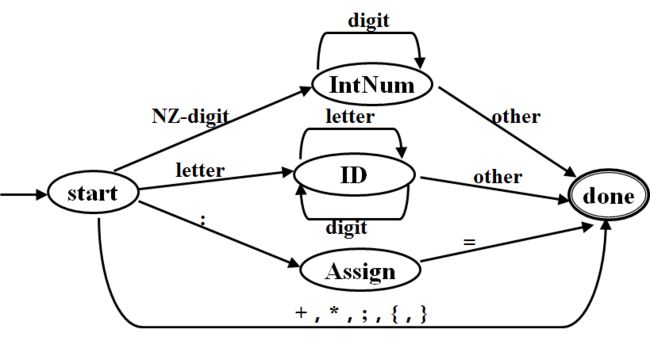
保留字/关键字 会被判定，通过在标识符的部分检查保留字/关键字表

输入：一个符号小序列，在序列结尾是EOF
输出：词法单元序列

词法单元数据结构：
struct Token{
 TkType type;
 char val[50];
}

预定义函数

• bool ReadNextchar()  读取流字符中的流符号，如果符号是EOF返回false，否则返回true

• int IsKeyword(str)   检查str是否是关键字中的一个，如果是，返回关键字的编码,否则返回-1

• void SkipBlank()   跳过空白符和return直到读到了流字符的另一个符号

  
  

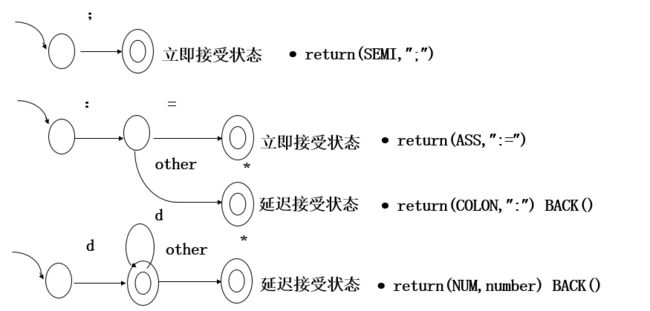
    SkipBlank();
    start:     case CurrentChar of
    “1..9”: str[len] = CurrentChar; len++;  goto IntNum ;
    “a..z”, “A..Z”: str[len] = CurrentChar; len++; goto ID;
    “:”: goto Assign;
    “+” : tk.type =PLUS; SkipBlank() ;goto Done;
    “*”: tk.type = MINUS; SkipBlank() ;goto Done;
    “;” :tk.type = SEMI ; SkipBlank() ;goto Done;
    EOF: exit;
    other: error();
    
    IntNum:
    if  (not ReadNextchar())
    {if len !=0 {tk.type = NUM, strcpy(tk.val, str);
    goto Done}}
    case CurrentChar of
    “0..9”: str[len] = CurrentChar; len++; goto IntNum ;
    other:  tk.type = NUM, strcpy(tk.val, str);
    
    ID:
    if  (not ReadNextchar())
    {if len !=0 {tk.type = IDE, strcpy(tk.val, str);
    goto Done}}
    case CurrentChar of
    “0..9”: str[len] = CurrentChar; len++; goto ID;
    “a..z”, “A..Z”: str[len] = CurrentChar; len++; goto ID;
    other: if  IsKeyword(str)
    {tk.type = IsKeyword(str) }
    else  {tk.type = IDE, strcpy(tk.val, str) };
    goto done;
    
    Assign:
    if  (not ReadNextchar())  {if len !=0 error; exit;};
    case CurrentChar of
    “=”: Tk.type = ASS;
    goto Done ;
    other:error();
  
    Done:
    TokenList[total] = tk;              // add new token to the token list
    total ++;                                    //
    len = 0;                                     //start storing new token string
    strcpy(str, “”);                        // reset the token string
    SkipBlank();                          // skip blank characters
    goto start;                               //start scanning new token
  

  
  

上面这个词法分析器的问题是

1. str和词法单元序列使用了数组，是不实用的
2. 没有处理错误
3. 没有处理行号

编译原理——词法分析器实现

根据上面这个词法分析器做了一些小改动，但是依旧不完善

修改代码（不完整）

词法分析器的生成器Lex

flex是由自由软件基金会(Free Software Foundation)制作的GNU编译器包发布的，可以从Internet上免费获得;

课后PPT习题

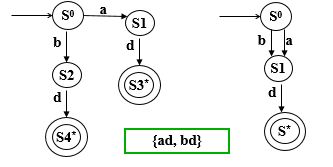
1. 画出与正则表达式a（ab|c）*等价的确定有限自动机。
2. 请用状态分离法将下面的DFA化简请用状态分离法将下面的DFA化简。
3. 给出自动机DFA的正则表达式。给出自动机DFA的正则表达式。

第二题图

第三题图