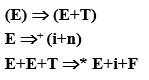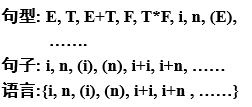编译原理——语法分析
根据上课内容顺序写的博客,并不是按照书的目录来的
使用龙书以及编译程序设计原理(第二版)金成植、金英编著
老师的PPT是英文的,我自己随便翻的,不一定对
文章目录
- 语法分析parsing
- 语法分析过程
- 语法分析基础知识
- 语法分析方法分类
- 上下文无关文法
- 什么是文法
- 乔姆斯基文法分类
- 上下文无关文法
- 例子
- 语法分析书和抽象语法树
- 语法树
- 二义性
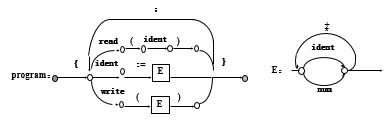
- 简单语言的语法
语法分析parsing
语法分析过程
语法分析基础知识
语法分析器的功能
输入:词法单元/词法单元序列
输出:语法结构的内在表达式
过程:
读取词法单元
生成语法结构——语法树,根据语法定义(上下文无关文法)
检查语法错误
语法结构
用来描述一个明确定义的程序的结构
- 程序
- 声明
常数声明
类型声明
变量声明
程序/函数声明 - 主体
- 声明(赋值,条件语句,循环,函数调用)
- 表达式(算数,逻辑,布尔)
语法错误
不同类型的语法错误:
处理语法错误:
- 立即退出,不实际
- 错误恢复
- 错误修补
- 错误改正
- 没有完美的办法
语法分析方法分类
通用于任何语法的语法分析方法(低效)
Cocke-Younger-Kasami算法
Earley’s 算法
自顶向下语法分析方法(有限制,可预测的)
递归下降法 recursive descendent parsing
LL(K) – K=1
自底向上语法分析方法(有限制,归约)
SLR(k)
LR(k)
LALR(k)
简单优先关系法
上下文无关文法
什么是文法
文法是表示无穷字符串集的强有力的一种有限方式
文法G (VT, VN, S, P)
VT 是一个有限的终极符集合
VN是一个有限的非终极符集合
S是文法的开始符
P是产生式的集合
每个生成规则都有以下形式
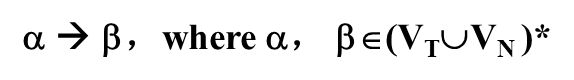
乔姆斯基文法分类
文法的分类
- O型文法: 也称为短语文法,其产生式具有形式:
- α→β,其中α,β∈(VT∪VN)*,并且α至少含一个非终极符;
- 1型文法: 也称为上下文有关文法。其产生式形式为:
- αAβ→αuβ,A∈VN,u为非空串,它是0型文法的特例,即要求|α| ≤ |β|;
- 2型文法: 也称为上下文无关文法。
- 它是1型文法的特例,即要求产生式左部是一个非终极符: A→β
- 3型文法: 也称为正则文法。
- 它是2型文法的特例,即其产生式的右部至多有两个符号,而且具有下面形式之一:
- A →a ,A →a B, 其中A,B∈VN ,a∈VT
上下文无关文法与正则表达式
正则表达式(a|b)*abb
文法:A0 → aA0|bA0|aA1
A1 → bA2
A2 →bA3
A3→ ε
文法的分类
描述能力
0型文法 > 1型文法 > 2型文法 > 3型文法
对应自动机
0型文法:图灵机
1型文法:线性有界自动机
2型文法:下推自动机
3型文法:有限自动机
上下文无关文法
上下文无关文法
Context Free Grammar(CFG)
定义为四元组(VT,VN,S,P)
VT是有限的终极符集合
VN是有限的非终极符集合
S是开始符,S∈ VN
P是产生式的集合,且具有下面的形式:
A→X1X2…Xn
其中A∈VN,Xi∈ (VT∪VN) ,右部可空。
一些通常的符号变量
通常情况下
- {A,B,…,Z}用来表示非终极符
- {a,b,…,z}用来表示终极符
- {α,β,…}用来表示字符串
- ε用来表示空字符串
推导
如果有一个产生式A→β,我们得到αAγ=>αβγ =>代表用A→β一步推导
我们可以说αβγ 是αAγ推导的
=>的含义是,使用一条规则,代替=>左边的某个符号,产生=>右端的符号串
扩展巴克斯范式
文法转换的一些算法
文法等价变化:L(G1)=L(G2)
增补文法(增光文法):开始符不能出现在产生式的右侧
Z→S
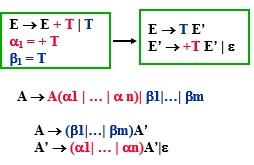
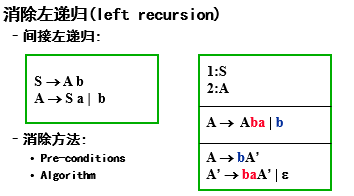
消除公共前缀
公共前缀 A→αβ1| … | αβn | γ1 | … | γm
提取公因子 A→αA’ | γ1 | … | γm A’ → β1 | … | βn
例子
例子1
VT={i, n, +, , (, )}
VN={E, T, F}
S=E
P:{ E→T E→E+T T→F T→TF F→(E) F→i F→n }
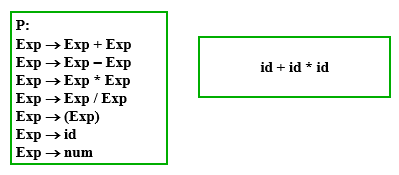
例子2
算术表达式
VT={id, num, (, ), +, -, *, /}
VN={Exp}
S=Exp
P:{ Exp→Exp+Exp Exp→Exp-Exp Exp→Exp * Exp Exp→Exp/Exp Exp→(Exp) Exp→id Exp→num }
例子3
程序
VT={VarDec, TypeDec, ConstDec, MainFun, FunDec}
VN={Program, Dec, Decs}
S=Program
P:{ Program→Dec MainFun Decs Dec→ε Dec→VarDec Dec→ConstDec Dec→FunDec Dec→TypeDec Decs→Dec Decs→Decs;Dec}
语法分析书和抽象语法树
问题:推导是从开始符构造一个句子的方法
许多推导来自同一个句子
不能唯一地代表句子的结构
语法书:表示一个句子的结构的方法
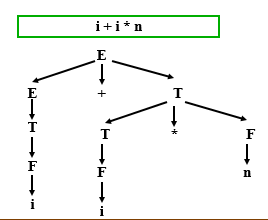
语法树
一颗使用上下文无关文法的有标号树
根必须是开始符的标号
每一个节点都是一个与之相关联的符号
每个叶子必须是一个终极符的标签
对于每一个与非终极符A相关的节点,都有n个儿子,从左到右他们一起与符号B1,B2,…,Bn相关,必须有个产生式A→B1B2…Bn
二义性
二义性文法
对于一个文法G,如果存在一个句子有不止一颗语法树,G被称为二义性文法
二义性文法是不可判定的
解决方案1:重写文法
解决方案2:制定一个语法分析树作为推荐的