深度学习中的线性代数知识详解

1. 基础概念

标量(scalar)
一个标量就是一个单独的数，一般用小写的的变量名称表示。

向量(vector)
一个向量就是一列数，这些数是有序排列的:

⎡⎣⎢⎢⎢⎢x1x2...x5⎤⎦⎥⎥⎥⎥ [ x 1 x 2 . . . x 5 ]

矩阵(matrices)
矩阵是二维数组:

⎡⎣⎢⎢⎢⎢a11a21...am1a12a22...am2.........a1na2n...amn⎤⎦⎥⎥⎥⎥ [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . a m 1 a m 2 . . . a m n ]

张量(tensor)
多维数组中元素分布在若干位坐标的规则网络中, 称之为张量. 几何代数中定义的张量是基于向量和矩阵的推广，通俗一点理解的话，我们可以将标量视为零阶张量，矢量视为一阶张量，那么矩阵就是二阶张量。
张量在深度学习中是一个很重要的概念，因为它是一个深度学习框架中的一个核心组件，后续的所有运算和优化算法几乎都是基于张量进行的。

2. 矩阵相关

转置(transpose)
主对角线: 矩阵从左上角到右下角的对角线称为主对角线.矩阵的转置是指以主对角线为轴的镜像.
令矩阵 A A 的转置表示为 AT A T , 则定义如下:

((A)T)i,j=Ai,j ( ( A ) T ) i , j = A i , j

Tips:
向量是 单列矩阵, 向量的转置是 单行矩阵. 标量可看做 单元素矩阵, 因此标量的转置是它本身: a=aT a = a T .

矩阵加法和广播:
矩阵加法定义: C=A+B C = A + B

在深度学习中, 允许矩阵和向量相加, 产生一个新的矩阵, 简写为: C=A+b C = A + b , 表示向量 b b 和矩阵 A A 的每一行都相加. 这种隐式地幅值向量 b b 到很多位置的方式成为广播.

矩阵乘法
分配律: A(B+C) A ( B + C )
结合律: A(BC)=(AB)C A ( B C ) = ( A B ) C
矩阵乘积不满足交换律: AB≠BA A B ≠ B A
向量点积满足交换律: xTy=yTx x T y = y T x
乘积的转置: (AB)T=BTAT ( A B ) T = B T A T

单位矩阵
主对角线元素都是1, 其余位置所有元素都是0的矩阵:

⎛⎝⎜⎜100010001⎞⎠⎟⎟ ( 1 0 0 0 1 0 0 0 1 )

我们将n维向量不变的单位矩阵即为 In I n :

∀x∈Rn,Inx=x,其中In∈Rnxn ∀ x ∈ R n , I n x = x , 其 中 I n ∈ R n x n

逆矩阵
矩阵逆是强大的工具, 对于大多数矩阵, 都可以通过矩阵逆解析求 Ax=b A x = b 的解.
矩阵 A A 的矩阵逆记作: A−1 A − 1 , 矩阵逆满足如下条件:

A−1A=In A − 1 A = I n

3. 线性相关

线性方程:

X⋅b⃗ =y⃗  X ⋅ b → = y →

线性组合: X 中各个列向量乘以对应的系数之和:

∑ibix(i) ∑ i b i x ( i )

生成空间: X中的原始向量线性组合后能抵达的点的集合. 确定上述方程是否有解相当于确定向量 y⃗  y → 是否在X 的列向量的生成子空间中.

矩阵X可逆时解为 b⃗ =X−1⋅y b → = X − 1 ⋅ y , 然而矩阵可逆是一个十分苛刻的条件,X 的列空间构成整个m维欧式空间 Rm R m , 若 X⋅b⃗ =y⃗  X ⋅ b → = y → 对于每一个y值最多有一个解, 则X矩阵至多有m个列向量.

因此, 矩阵X只有是方阵且所有列向量都是线性无关的时候才满足要求, 若列向量线性相关, 则成该方阵X是奇异的.

这里引出了线性模型的基本模型:

X⋅b⃗ =y⃗  X ⋅ b → = y →

X可逆时 ,我们可以直接对两边求逆, 得到线性模型的唯一解:

b⃗ =X−1⋅y b → = X − 1 ⋅ y

然而,样本特征组成的矩阵X往往是不可逆的, 即X往往不是方阵, 或者是奇异的方阵.

正因为在现实世界里, 直接对矩阵求逆来得到唯一解 b⃗  b → 几乎是不可能的, 所以我们才会退而求其次, 用最小化误差来逼近唯一解, 这叫做松弛求解.

求最小化误差的一般方法是求残差的平方和最小化, 这也就是所谓的线性最小二乘法.

4. 范数(norm)

在机器学习中, 通常用范数来衡量一个矩阵的大小, Lp L p 范数公式:

||x||p=(∑i|xi|p)1p | | x | | p = ( ∑ i | x i | p ) 1 p

注意抓重点: 范数在机器学习中是用来衡量一个向量的大小.

范数: 是将向量映射到非负值的函数. 简单来讲, 向量 x⃗  x → 的范数是原点到 x⃗  x → 的距离. 这里之所以介绍范数, 是因为它涉及到机器学习中非常重要的正则化技术.

p=2 p = 2 时, L2 L 2 称为欧几里得范数(Euclidean norm), 表示原点到向量 x⃗  x → 的欧氏距离, L2 L 2 范数通常简写为 ||x|| | | x | | , 它非常频繁地出现在机器学习中. 此外, 平方 L2 L 2 范数 (||x||)2 ( | | x | | ) 2 也经常用来衡量向量的大小, 可以简单地用点积 (x⃗ )⊤⋅x⃗  ( x → ) ⊤ ⋅ x → 计算.

L2 L 2 范数:

||x||2=(∑i|xi|2)12 | | x | | 2 = ( ∑ i | x i | 2 ) 1 2

平方 L2 L 2 范数:

||x||=∑i|xi|2 | | x | | = ∑ i | x i | 2

L1 L 1 范数:

||x||1=∑i|xi| | | x | | 1 = ∑ i | x i |

Frobenius范数:

||A||F=∑i,jAi,j2‾‾‾‾‾‾‾√ | | A | | F = ∑ i , j A i , j 2

关于范数, 注意以下几点:
- 平方 L2 L 2 范数对 x⃗  x → 各元素导数只和对应元素相关, 而 L2 L 2 范数对个元素的导数和整个向量相关, 因此平方 L2 L 2 范数计算更方便.

• 有时候平方 L2 L 2 范数在原点附近增长缓慢, 在某些机器学习业务场景下, 区分元素值是否非零很重要, 此时更倾向于使用 L1 L 1 范数.

• L1 L 1 范数在各个位置斜率相同, 且数学形式较简单, 每当 x⃗  x → 中某元素从0增加了 ϵ ϵ 时, 对应 L1 L 1 范数也增加 ϵ ϵ , L1 L 1 范数通常被用在零和非零差异非常重要的机器学习问题中.

• “ L0 L 0 范数”通常用向量中非零元素个数来衡量向量大小, 但是这种说法不严谨, 因为从数学意义上讲,对向量缩放 α α 倍, 向量大小会变, 但是机器学习中, 非零元素数目不变, 这和向量运算的数学意义相悖.

• L∞ L ∞ 范数称为最大范数(max norm), 表示最大幅值元素的绝对值: ||x||∞=maxi|xi| | | x | | ∞ = max i | x i |

• Frobenius范数在机器学习中用来衡量矩阵大小.

• 两个点积可以用范数来表示: x⃗ T⋅y⃗ =||x⃗ ||2||y⃗ ||2cosθ x → T ⋅ y → = | | x → | | 2 | | y → | | 2 c o s θ

在机器学习中, L2 L 2 和 L1 L 1 范数分别对应 L2 L 2 和 L1 L 1 正则化, 详情参考线性模型中的岭回归(Ridge Regression)和套索回归(Lasso).

5. 伪逆(Moore-Penrose)

非方阵方程,其逆矩阵没有意义. 假设要求解线性方程

A⃗ ⋅x=y⃗  A → ⋅ x = y →

等式两边左乘左逆 B⃗  B → 后:

x=B⃗ y x = B → y

是否存在唯一映射, 将 A⃗  A → 映射到 B⃗  B → 取决于问题形式:
1. 若矩阵A行数大于列数, 则可能无解;
2. 若矩阵A行数小于列数, 则可能有多个解.

伪逆可以解决上述问题. 矩阵A的伪逆定义为:

lima↘0(AT→A⃗ +αI⃗ )−1⋅AT→ lim a ↘ 0 ( A T → A → + α I → ) − 1 ⋅ A T →

违逆计算的简化公式为:

A+→=V⃗ D+→UT→ A + → = V → D + → U T →

其中, 矩阵U, D, V是矩阵A的 奇异值分解后的特殊矩阵, 其中 U⃗  U → 和 V⃗  V → 都是 正交矩阵, D⃗  D → 为 对角矩阵(不一定是方阵). 对角矩阵D的 伪逆 D+→ D + → 是非零元素取倒数后再转置得到的.奇异值分解称为 SVD(Singular Value Decomposition).

1. 矩阵A的列数多于行数时, 可能有多个解. 伪逆求解线性方程是众多解法中的一种, 即: x⃗ =A+→y⃗  x → = A + → y → 是所有可行解中欧几里得距离最小的一个
2. 矩阵A列数小于行数时, 可能没有解. 伪逆求解得到的x是 A⃗ x A → x 和 y⃗  y → 的欧几里得距离 ||A⃗ x−y⃗ ||22 | | A → x − y → | | 2 2 最小的解, 这里又回到了求解线性问题的一般思路上: 线性最小二乘法.

6. 常用的距离

1、曼哈顿距离
也称为城市街区距离，数学定义如下：

d=∑k=1n|x1k−x2k| d = ∑ k = 1 n | x 1 k − x 2 k |

曼哈顿距离的Python实现：

from numpy import *
vector1 = mat([1,2,3])
vector2 = mat([4,5,6])
print sum(abs(vector1-vector2))

2. 欧氏距离
前面提到过, 欧氏距离就是 L2 L 2 范数, 定义如下:

d=∑k=1n(x1k−x2k)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾⎷ d = ∑ k = 1 n ( x 1 k − x 2 k ) 2

欧氏距离的Python实现：

vector1 = np.mat([1,2,3])
vector2 = np.mat([4,5,6])
print np.sqrt((vector1-vector2)*(vector1-vector2).T)

3. 闵可夫斯基距离
上述两种距离的更一般形式, 完整的定义如下:

d=∑k=1n(x1k−x2k)p‾‾‾‾‾‾‾‾‾‾‾‾‾‾⎷p d = ∑ k = 1 n ( x 1 k − x 2 k ) p p

4. 切比雪夫距离
即前面提到过的无穷范数 L∞ L ∞ 范数, 数学表达式:

d=max(|x1k−x2k|) d = m a x ( | x 1 k − x 2 k | )

Python实现如下

from numpy import *
vector1 = mat([1,2,3])
vector2 = mat([4,5,6])
print sqrt(abs(vector1-vector2).max)

5. 夹角余弦

用来衡量两个向量方向的差异, 夹角余弦越大，表示两个向量的夹角越小
机器学习中用这一概念来衡量样本向量之间的差异，其数学表达式如下:

cosθ=AB|A||B|=∑nk=1x1k⋅x2k∑nk=1x21k‾‾‾‾‾‾‾‾√⋅∑nk=1x22k‾‾‾‾‾‾‾‾√ c o s θ = A B | A | | B | = ∑ k = 1 n x 1 k ⋅ x 2 k ∑ k = 1 n x 1 k 2 ⋅ ∑ k = 1 n x 2 k 2

python实现:

from numpy import *
vector1 = mat([1,2,3])
vector2 = mat([4,5,6])
print dot(vector1,vector2)/(linalg.norm(vector1)*linalg.norm(vector2))

6. 汉明距离
表示两个字符串中不相同位数的数目, 例如：字符串‘1111’与‘1001’之间的汉明距离为2.
信息编码中一般应使得编码间的汉明距离尽可能的小.
python实现:

from numpy import *
matV = mat([1,1,1,1],[1,0,0,1])
smstr = nonzero(matV[0]-matV[1])
print smstr

7. 杰卡德距离
杰卡德相似系数: 两个集合A和B的交集元素在A和B的并集中所占的比例称为两个集合的杰卡德相似系数，用符号 J(A,B) J ( A , B ) 表示.
数学表达式:

J(A,B)=∣∣A⋂B∣∣∣∣A⋃B∣∣ J ( A , B ) = | A ⋂ B | | A ⋃ B |

杰卡德距离: 用杰卡德相似系数来描述, 用符号 Jσ J σ 表示.
数学表达式:

Jσ=1−J(A,B)=∣∣A⋃B∣∣−∣∣A⋂B∣∣∣∣A⋃B∣∣ J σ = 1 − J ( A , B ) = | A ⋃ B | − | A ⋂ B | | A ⋃ B |

Python实现：

from numpy import *
import scipy.spatial.distance as dist
matV = mat([1,1,1,1],[1,0,0,1])
print dist.pdist(matV,'jaccard')

7. 特征分解

许多数学对象可以通过将它们分解成多个组成部分。特征分解是使用最广的矩阵分解之一，即将矩阵分解成一组特征向量和特征值。

方阵A的特征向量是指与A相乘后相当于对该向量进行缩放的非零向量 ν ν ：

Aν=λν A ν = λ ν

标量 λ λ 被称为这个特征向量对应的特征值。

使用特征分解去分析矩阵A时，得到特征向量构成的矩阵V和特征值构成的向量 λ λ ，我们可以重新将A的特征分解记作：

A=Vdiag(λ)V−1 A = V d i a g ( λ ) V − 1

每个实对称矩阵都可以分解成实特征向量和实特征值: A=QΛQT A = Q Λ Q T
Q Q 是 A A 的特征向量组成的正交矩阵， Λ Λ 是对角矩阵

任意一个实对称矩阵 A 都有特征分解，但是特征分解可能并不唯一.
矩阵是奇异的当且仅当含 有零特征值.

正定矩阵: 所有特征值都是正数的矩阵.
负定矩阵: 所有特征值都是负数的矩阵.
半正定矩阵: 所有特征值都是非负数的矩阵.

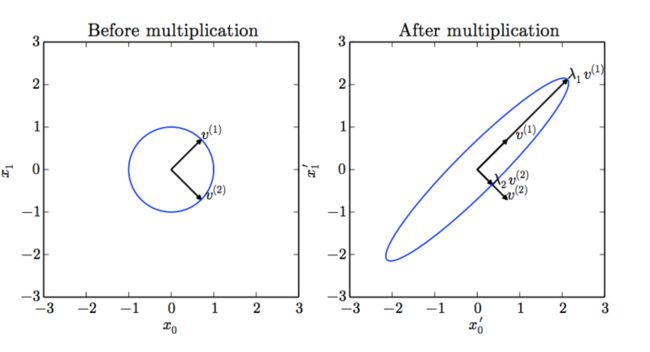
下图展示了特征值和特征向量的作用效果:

在上图中，矩阵 A A 有两个标准正交的特征向量，对应特征值为 λ1 λ 1 的 v(1) v ( 1 ) 以及对应特征值为 λ2 λ 2 的 v(2) v ( 2 ) 。(左) 我 们画出了所有的单位向量 u∈R2 u ∈ R 2 的集合，构成一个单位圆。(右) 我们画出了所有的 Au A u 点的集 合。通过观察 A A 拉伸单位圆的方式，我们可以看到它将 v(i) v ( i ) 方向的空间拉伸了 λi λ i 倍.

8. 奇异值分解(SVD)

除了特征分解，还有一种分解矩阵的方法，被称为奇异值分解（SVD）。将矩阵分解为奇异向量和奇异值。通过奇异分解，我们会得到一些类似于特征分解的信息。然而，奇异分解有更广泛的应用。

每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这时我们只能使用奇异值分解。
奇异分解与特征分解类似，只不过这回我们将矩阵A分解成三个矩阵的乘积：

A=UDVT A = U D V T

假设A是一个 m×n m × n 矩阵，那么U是一个 m×m m × m 矩阵，D是一个 m×n m × n 矩阵，V是一个 n×n n × n 矩阵。

这些矩阵每一个都拥有特殊的结构，其中U和V都是正交矩阵，D是对角矩阵（注意，D不一定是方阵）。对角矩阵D对角线上的元素被称为矩阵A的奇异值。矩阵U的列向量被称为左奇异向量，矩阵V 的列向量被称右奇异向量。

SVD最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。另外，SVD可用于推荐系统中。