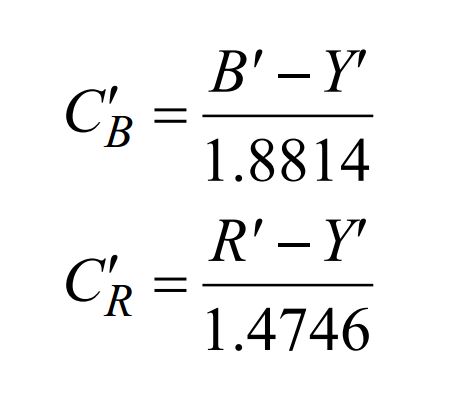YUV与RGB互转各种公式 (YUV与RGB的转换公式有很多种,请注意区别!!!)
一、 公式:基于BT.601-6
BT601 UV 的坐标图(量化后): (横坐标为u,纵坐标为v,左下角为原点)
通过坐标图我们可以看到UV并不会包含整个坐标系,而是呈一个旋转了一定角度的八边形, U越大蓝色越蓝,V越大,红色越红。
名词解释:
量化后: Y~(16,235) U ~(16-240) V~(16-240) 量化就是让通过线性变换让Y 或 U 或V 处于一定的范围内, 比如让Y (0,255) 变到 Y' (16,235) 就这样来实行: Y' = Y*[(235-16)/255] +16
未量化: Y/U/V ~(0-255)
YUV :即 YCbCr 两者是等价的
1.小数形式,未量化
R = Y + 1.4075 * (V-128);
G = Y - 0.3455 * (U-128) - 0.7169*(V-128);
B = Y + 1.779 * (U-128);
Y = 0.299*R + 0.587*G + 0.114*B;
U = (B-Y)/1.772;
V = (R-Y)/1.402; (U~(-128-127))
或写为:
Y = 0.299*R + 0.587*G + 0.114*B;
U = -0.169*R - 0.331*G + 0.5 *B ;
V = 0.5 *R - 0.419*G - 0.081*B;
2.整数形式(减少计算量)未量化
R= Y + ((360 * (V - 128))>>8) ;
G= Y - (( ( 88 * (U - 128) + 184 * (V - 128)) )>>8) ;
B= Y +((455 * (U - 128))>>8) ;
Y = (77*R + 150*G + 29*B)>>8;
U = ((-44*R - 87*G + 131*B)>>8) + 128;
V = ((131*R - 110*G - 21*B)>>8) + 128 ;
3. 量化后的公式( Y~(16,235) U/V ~(16,240) ) 量化
yuv --> rgb
R = 1.164*Y + 1.596 * V - 222.9
G = 1.164*Y - 0.392 * U - 0.823 * V+ 135.6
B = 1.164*Y + 2.017 * U- 276.8
rgb --> yuv
Y = 0.257*R' + 0.504*G' + 0.098*B' + 16
U = -0.148*R' - 0.291*G' + 0.439*B' + 128
V = 0.439*R' - 0.368*G' - 0.071*B' + 128
由此可以得到
R = ( 81,91,240 )
下图为bt601文档上的截图 : 截图1 截图2
4 量化后的公式写成整数的形式(减小计算量) ( Y~(16,235) U/V ~(16,240) )
yuv --> rgb
R = (298*Y + 411 * V - 57344)>>8
G = (298*Y - 101* U - 211* V+ 34739)>>8
B = (298*Y + 519* U- 71117)>>8
rgb --> yuv
Y= ( 66*R + 129*G + 25*B)>>8 + 16
U= (-38*R - 74*G + 112*B)>>8 +128
V= (112*R - 94*G - 18*B)>>8 + 128
5. YUV量化 与 非量化 互转
YUV 量化 转 非量化
Y=(Y'-16 )*255/219 ;
U=(U'-128)*128/112;
V=(V'-128)*128/112;
YUV 量化 转 非量化 U~(-128-127) -----> U~(16-240)
Y' = ((219*Y)>>8) + 16;
U' = ((219*U)>>8) + 128;
V' = ((219*V)>>8) + 128;
6. YV12 转RGB (这个有待考证。。!!)
R = Y + 1.370705 * ( V - 128 ) ; // r分量值
G = Y - 0.698001 * ( U - 128 ) - 0.703125 * (V - 128) // g分量值
B = Y + 1.732446 * ( U - 128 ); // b分量值
7. 矩阵形式(BT601):
矩阵形式
量化前
[Y,U,V]T = M[R,G,B]T 其中 M = 0.299 , 0.587, 0.114, -0.169, - 0.331, 0.5, 0.5, - 0.419 - 0.081
[R,G,B]T = M[Y,U,V]T 其中 M = 1 0 1.4017 1 -0.3437 -0.7142 1 1.7722 0
量化后
[Y,U,V,1]T = M[R,G,B,1]T 其中 M = [ 0.2568, 0.5041, 0.0979, 16 -0.1479, -0.2896, 0.4375, 128 0.4375, -0.3666, -0.0709, 128, 0, 0, 0, 1 ]
[R,G,B,1]T = M[Y,U,V,1]T M = 1.1644 0 1.6019 -223.5521 1.1644 -0.3928 -0.8163 136.1381 1.1644 2.0253 0 -278.0291 0.0000 0.0000 0.0000 1.0000
量化后的公式写成整数形式
[Y,U,V,1]T = (M[R,G,B,1]T)>>8 其中 M = 66, 129, 25, 4096, -38, -74, 112, 32768, 112, -94, -18, 32768, 0, 0, 0, 256
[R,G,B,1]T = (M[Y,U,V,1]T)>>8 M = 298, 0, 410, -57229, 298, -101, -209, 34851, 298, 518, 0, -71175, 0, 0, 0, 256
二、. Rec2020 (BT2020) 下的YUV与RGB转换公式 (我觉得还是写成矩阵的形式更加统一协调)
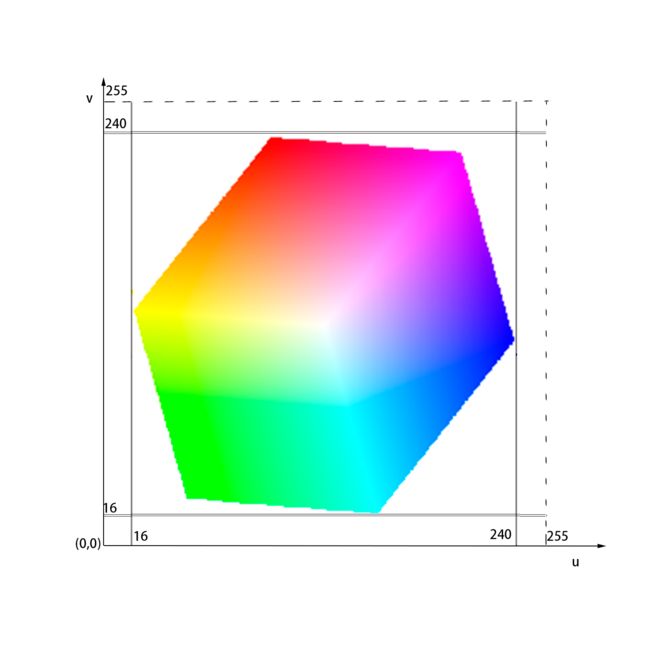
BT2020 UV 的坐标图(量化后): (横坐标为u,纵坐标为v,左下角为原点)
通过坐标图我们可以看到UV不同于BT601协议,该uv代表的颜色范围更大,该颜色范围呈一个不规则八边形。
1. full range
即:
Y = 0.2627*R + 0.6780*G + 0.0593*B;
U = -0.1396*R - 0.3604*G + 0.5*B;
V = 0.5*R - 0.4598*G -0.0402*B;
矩阵形式
量化前
[Y,U,V]T = M[R,G,B]T 其中 M = 0.2627 0.6780 0.0593 , -0.1396 -0.3604 0.5000, 0.5000 -0.4598 -0.0402
[R,G,B]T = M[Y,U,V]T 其中 M = 1.0000 -0.0000 1.4746 1.0000 -0.1645 -0.5713 1.0000 1.8814 -0.0001
量化后
[Y,U,V,1]T = M[R,G,B,1]T 其中 M = 0.2256, 0.5823, 0.05093, 16, -0.1222, -0.3154, 0.4375, 128 , 0.4375, -0.4023, -0.0352, 128, 0,0,0,1
[R,G,B,1]T = M[Y,U,V,1]T M =1.1644, 0, 1.6853, -234.3559, 1.1644, -0.1881, -0.6529, 89.0206, 1.1646, 2.1501, 0.0000, -293.8542, 0.0000, 0.0000, 0.0000, 1.0000
量化后的公式写成整数形式
[Y,U,V,1]T = (M[R,G,B,1]T)>>8 其中 M = 58, 149, 13, 4096, -31, -81, 112, 32768, 112, -103, -9, 32768, 0, 0, 0, 256
[R,G,B,1]T = (M[Y,U,V,1]T)>>8 M = 298, 0, 431, -59995, 298, -48, -167, 22789, 298, 550, 0, -75227, 0, 0, 0, 256
2. BT601 转 BT2020
_Y = (256*Y - 32*U -30*V+ 7826)>>8;
_U = (258*U +17*V - 2208)>>8;
_V = (22*U + 264*V - 3369)>>8;
RGB与HSV互转
1.RGB转HSV
1: max=max(R,G,B) 2: min=min(R,G,B) 3: if R = max, H = (G-B)/(max-min) 4: if G = max, H = 2 + (B-R)/(max-min) 5: if B = max, H = 4 + (R-G)/(max-min) 6: 7: H = H * 60 8: if H < 0, H = H + 360 9: 10: V=max(R,G,B) 11: S=(max-min)/max |
2. HSV转RGB
1: if s = 0 2: R=G=B=V 3: else 4: H /= 60; 5: i = INTEGER(H) 6: 7: f = H - i 8: a = V * ( 1 - s ) 9: b = V * ( 1 - s * f ) 10: c = V * ( 1 - s * (1 - f ) ) 11: 12: switch(i) 13: case 0: R = V; G = c; B = a; 14: case 1: R = b; G = v; B = a; 15: case 2: R = a; G = v; B = c; 16: case 3: R = a; G = b; B = v; 17: case 4: R = c; G = a; B = v; 18: case 5: R = v; G = a; B = b; |