天池比赛-资金流入流出预测-挑战Baseline--时间序列初探

比赛地址在此：点击打开链接

起因：它这个项目是预测未来30天余额宝的总的申购总量和赎回总量，这个是跟余额宝的利率和上海银行间借拆利率有关。然而它30天后的这两个数值并没有给出，因此需要用时间序列来预测。

需要的工具库：

1.numpy  

2.pandas

3.statsmodels

4.matplotlib

第一步：读取数据

# 读取数据,并让report_date字段值成为index
date_interest=pd.read_csv(r'../analyed_data/date_interest.csv',index_col='report_date',parse_dates=['report_date'])
columns=date_interest.columns
# 因为有10个属性,所以需要每一个分开来进行预测
for i in range(len(columns)):
   print(date_interest.iloc[:,i].describe())

第二步:对数据进行统计分析

 主要步骤有：

 1.摘要分析

  2.画出时序图

 具体实现:

 1.首先实现绘制时序图的函数

def draw_trend(timeSeries,column): 
     f=plt.figure(facecolor='white')
     timeSeries=timeSeries.diff(3)
     timeSeries.plot(color='blue',label='timeSeries')
     plt.legend(loc='best')
     plt.title(column)
     plt.show()

 
 2.绘制时序图

date_interest=pd.read_csv(r'../analyed_data/date_interest.csv',index_col='report_date',parse_dates=['report_date'])
    columns=date_interest.columns
    for i in range(len(columns)):
        data=date_interest.iloc[:,i]
        column=columns[i]    
        # 绘制时序图
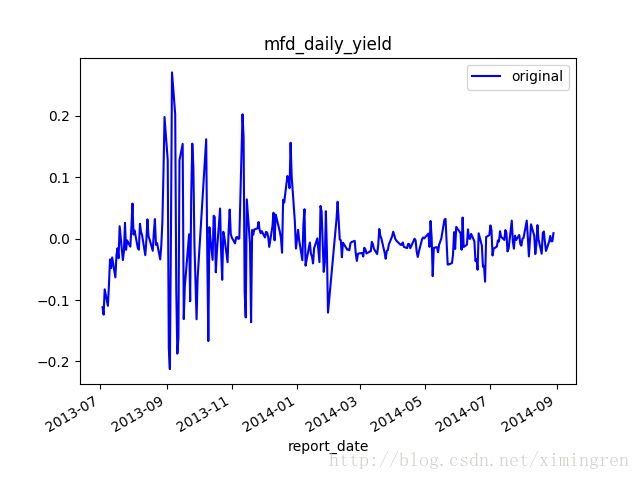
        draw_trend(data,column)

 

这里拿出一个图来展示一下,上图就是mdf_daily_yield这个属性它的时序图

 3.摘要统计

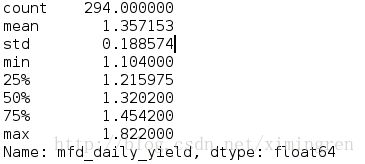
  这个就简单了,直接用describe函数简单看一下数值的情况

得到的结果如图所示.

第三步:实现ARMA模型

ARMA模型(自回归移动平均模型)需要三个参数,(p,d,q).在实现ARIMA模型之前,我们需要对序列的平稳性和白噪声进行检验,

这个被称为序列的预处理.首先来看一下序列的平稳性

 一:序列的预处理:

1.序列的平稳性:

 这里有两种方法可以检验平稳性,一个是观测法,另一个是单位根检验.

 1)观察法:

 所谓观察法就是根据序列的时序图来看序列是否平稳,比如上面我们得出的那个时序图,波动比较大,

暂时认为它不平稳.观察法受人的主观观念影响比较大.

因此我们选择另一种方法.

   2)单位根检验

  这里我们用到了statsmodels这个库,请确保下载了这个库.接着来实现单位根检验的函数.

# 单位根检验
def analyse_stationary(data,column):
    stationiary = (data)
    result = adfuller(stationiary)
    print(column)
    print("ADF  Statistic:%f" % result[0])
    print("p-value : %f" % result[1])
    print("Critical Values:")
    for key, value in result[4].items():
        print("\t %s: %.3f" % (key, value))

结果如下图所示.

可以看得出p值为0.6,比0.05大,说明不能否定原假设,这里的原假设是序列存在单位根,即意味着序列是不平稳的.

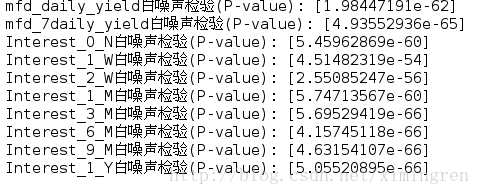
2.序列的白噪声检验:

 acorr_ljungbox(data, lags=1)[1]

 用这个函数就可以进行白噪声检验了.结果如下.

可以看出每个字段的检验p值都显著小于0.05,可以排除白噪声.

3.将非平稳序列转为平稳序列

 序列的平稳性是进行时间序列分析的前提,在大数定理和中心定理中要求样本同分布(这里同分布等价于时间序列中的平稳性),

而我们的建模过程有很多都是建立在大数定理和中心极限定理的前提条件下的,

如果它不满足,得到的许多结论都是不可靠的.(上面一段话是参考他人的)

 将非平稳序列转为平稳的常见方法就是差分,除此之外还有对数变换,平滑法和分解.这里我们用差分来进行转化.

 差分的操作很简单,用diff(n)函数就能实现,n是差分的阶数.进行差分后再次用单位根检验来看是否平稳.在这里我进行了一阶

差分后序列就变得平稳了.

二.模型识别

获得平稳和没有白噪声的序列之后,我们就要根据自相关图(acf)和偏自相关图(pacf)来确定p值和q值,即模型的定阶.我们可以用

statsmodels中的相关函数来绘制.

# 绘制acf和pacf图
# lags是多少阶的意思
def draw_acf_pacf(data,column):
    plt.subplot(211)
    plot_acf(data,ax=plt.gca(),lags=40)
    plt.subplot(212)
    plot_pacf(data,ax=plt.gca(),lags=40)
    plt.show()
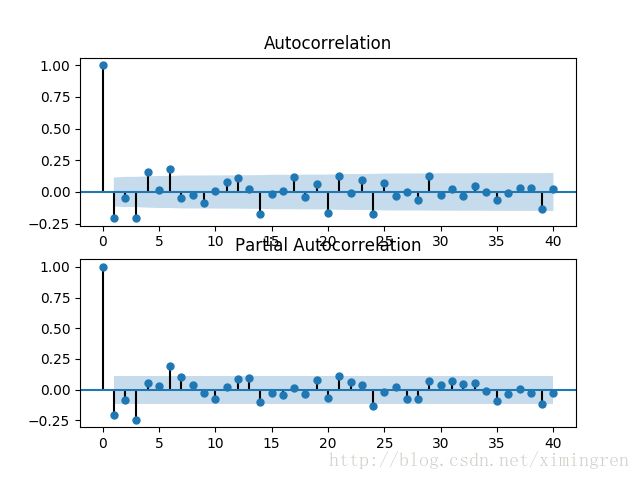
#经过对acf和pacf图的分析，大多数的属性都是拖尾，一阶相关性，少数是有截尾的

摘取其中一个字段的acf和pacf来定阶.

这里涉及到一个问题,如何根据acf和pacf定阶的问题.首先来看一下拖尾和截尾的概念.

拖尾是指acf或pacf在某阶后并不为0的性质.截尾即是指时间序列acf或pacf在某阶后均为0的性质

那么我们可以从上图看出,该字段的acf和pacf都存在拖尾的现象,并且存在1阶相关性.图的横坐标是阶数.我们暂时确定p和q值

均为1,后续我们可以用网格搜索法来有优化模型.

下面我们就来实现模型,并且绘制模型的预测值和实际值的差别图.

 model=ARMA(data_diff,order=(2,2)).fit(disp=0)
    # data_diff是进行一阶差分后的序列,disp参数设置为0是不显示运行信息的意思
    # 绘制出预测值与实际值的线图
    # predict_sunspots=model.predict()
    # # 去除没有预测的
    # data=data[predict_sunspots.index]
    # fig,ax=plt.subplots(figsize=(12,8))
    # ax=data.plot(ax=ax)
    # predict_sunspots.plot(ax=ax,color='red')
    # plt.show()

上图的红色线段是预测值,蓝色是实际值,可以看出误差很是挺大的.如果就想这样然后预测未来30天的序列的话,我们可以用以下

代码实现.

    predict_sunspots=model.forecast(steps=30)[0]

 本文就先到此,下次我们用网络搜索法来对ARMA模型进行优化.