Tensorflow 入门学习11.CNN卷积神经网络原理1.（卷积基本概念）

本文学习内容来自《TensorFlow深度学习应用实践》《深度学习》
卷积网络（convolutional network）（LeCun，1989），也叫作卷积神经网络（convolutional neural network，CNN），是一种专门用来处理具有类似网络结构的数据的神经网络。
它是从信号处理衍生过来的一种对数字信号处理的方式，发展到图像信号处理上演变成一种专门用来处理具有矩阵特征的网络结构处理方式。卷积神经网络在很多应用上都有独特的优势，如音频、图像处理。
“卷积神经网络”一词表明该网络使用了卷积（convolution）这种数学运算。卷积是一种特殊的线性运算。卷积网络是指那些至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。

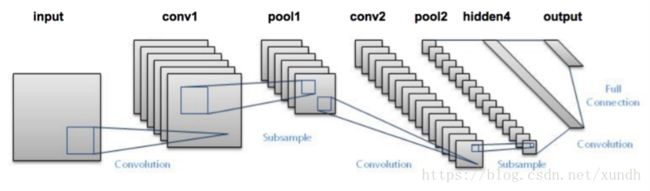
卷积神经网络结构

卷积运算基本概念

卷积运算通常用星号表示：
$$s(t)=(x\ast w)(t)$$
在卷积网络的术语中，卷积的第一个参数（在这个例子中，函数x）通常叫作输入，第二个参数叫作核函数。输出有时称作特征映射。

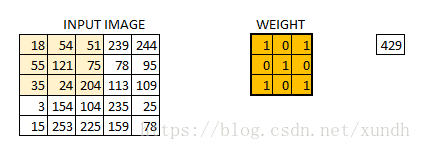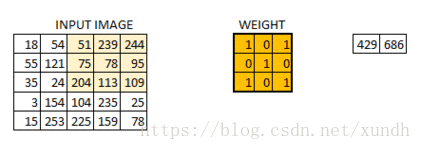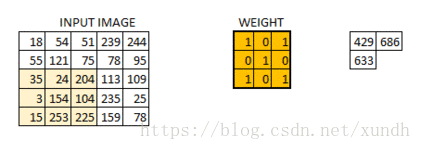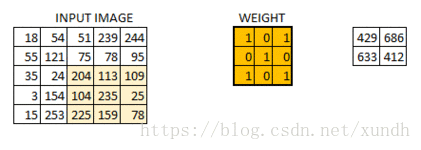
在数字图像处理中有一种最为基本的处理方法，即线性滤波。将待处理的二维数字看作一个大型矩阵，图像中的每个像素可以看作矩阵中的每个元素，像素的大小就是矩阵中的元素值。
而使用的滤波工具是另一个小型矩阵，这个矩阵被称为卷积核。卷积核的大小是远远小于图像矩阵，具体的计算方式就是对于图像大矩阵中的每个像素，计算其周围的像素和卷积核对应位置的乘积，之后将结果相加最终得到的终值就是该像素的值，这样就完成了一次卷积。

动机

有三个重要的思想用来帮助改进机器学习系统：稀疏交互、参数共享、等变表示。
数字图像处理卷积运算主要有两种思维，即“稀疏矩阵”与“参数共享”。
首先对于稀疏矩阵来说，卷积网络具有稀疏性，即卷积核的大小远远小于输入数据矩阵的大小。例如当输入一个图片信息时，数据的大小可能为上万的结构，但是使用的卷积核却只有几十，这样能够在计算后获取更少的参数特征，极大地减少了后续的计算量。

参数共享指的是在特征提取的过程中， 一个模型在多个参数之中使用相同的参数，在传统的神经网络中，每个权重只对其连接的输入输出起作用，当其连接的输入输出元素结束后就不会再用到。而参数共享指的是在卷积神经网络中核的每一个元素都被用在输入的每一个位置上，而在过程中学习一个参数集合就能把这个参数应用到所有的图片元素中。

Python 卷积示例

import numpy as np

dateMat = np.ones((7, 7))
print(dateMat)
kernel = np.array([[2, 1, 1], [3, 0, 1], [1, 1, 0]])
print(kernel)


def convolve(dateMat, kernel):
    m, n = dateMat.shape
    km, kn = kernel.shape
    newMat = np.ones(((m-km+1), (n-kn+1)))
    tempMat = np.ones(((km), (kn)))
    for row in range(m-km+1):
        for col in range(n-kn+1):
            for m_k in range(km):
                for n_k in range(kn):
                    tempMat[m_k, n_k] = dateMat[(row+m_k), (col+n_k)] * kernel[m_k, n_k]
            newMat[row, col] = np.sum(tempMat)
    return newMat

print(convolve(dateMat, kernel))

输出：

[[ 1.  1.  1.  1.  1.  1.  1.]
 [ 1.  1.  1.  1.  1.  1.  1.]
 [ 1.  1.  1.  1.  1.  1.  1.]
 [ 1.  1.  1.  1.  1.  1.  1.]
 [ 1.  1.  1.  1.  1.  1.  1.]
 [ 1.  1.  1.  1.  1.  1.  1.]
 [ 1.  1.  1.  1.  1.  1.  1.]]
[[2 1 1]
 [3 0 1]
 [1 1 0]]
[[ 10.  10.  10.  10.  10.]
 [ 10.  10.  10.  10.  10.]
 [ 10.  10.  10.  10.  10.]
 [ 10.  10.  10.  10.  10.]
 [ 10.  10.  10.  10.  10.]]

TensorFlow中卷积函数实现

tf.nn.conv2d

tf.nn.conv2d(input,filter,strides,padding,use_cudnn_on_gpu=None,name=None)

参数说明：

• input：指需要做卷积的输入图像，它要求是一个Tensor，具有[batch,in_height,in_width,in_channels]这样的shape，具体含义是[训练是一个batch的图片数量，图片高度，图片宽度、图像通道数]，注意这是一个四维的Tensor，要求类型为float32和float64其中之一。
• filter：相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height,filter_width,in_channels,out_channels]这样的shape，具体含义是[卷积核的高度、卷积核的宽度、图像的通道数、卷积核个数]，要求类型与参数input相同，有一个地方需要注意，第三维in_channels，就是参数input的第四维。
• strides：卷积时图像每一维的步长，这是一个一维的向量，第一维和第四维默认为1，而第三维和第四维分别是平等和竖直滑行的步进长度。
• padding：string类型的量，只能是"SAME","VALID"其中之一，这个值决定了不同的卷积方式。
• use_cudnn_on_gpu：是否使用gpu加速，默认true

strides

步长为一的卷积操作,不补零

**步长为2的卷积操作,不补零: **

padding 与步长

**padding=’SAME’ 时,TensorFlow会自动对原图像进行补零,从而使输入输出的图像大小一致 **

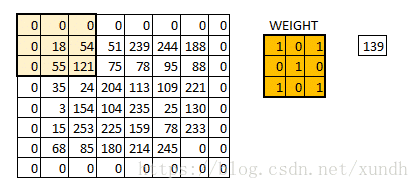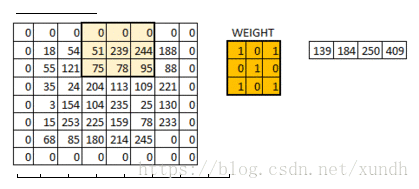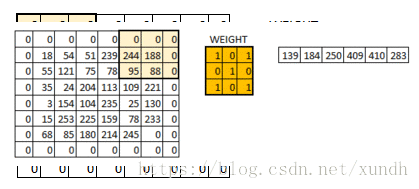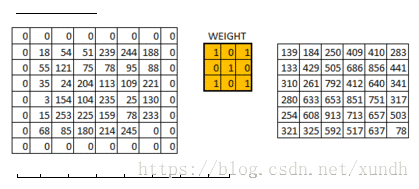
**padding=’VALLLD’ 时,则会缩小原图像的大小. **

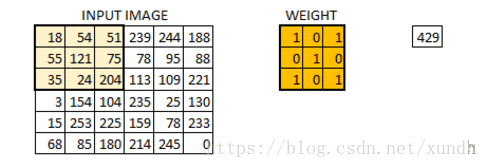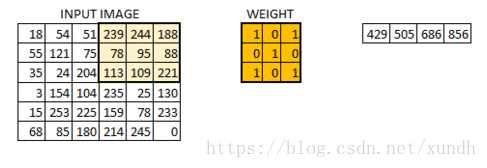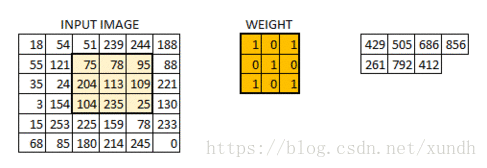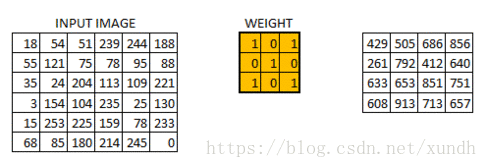
示例：

import tensorflow as tf

input = tf.Variable(tf.random_normal([1,3,3,1]))  # 输入张量的形状
filter= tf.Variable(tf.ones([1,1,1,1]))

init=tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    conv2d = tf.nn.conv2d(input, filter,strides=[1,1,1,1],padding='VALID')
    print(sess.run(conv2d))

输出结果是一个[3,3]的矩阵：

[[[[-0.62795395]
   [-0.70418018]
   [ 2.03271723]]

  [[-1.32693946]
   [ 1.19582796]
   [-0.44500229]]

  [[-1.23496175]
   [-0.34467456]
   [ 1.13358295]]]]

卷积在工作时，边缘被处理消失，因此生成的结果小于原有的图像。如果有时候需要生成的卷积结果和原输入矩阵的大小一致，则需要将参数padding的设为VALID，当其为SAME时，表示图像边缘将由一圈0补齐，使得卷积后的图像大小和输入大小一致。

tf.nn.depthwise_conv2d

input 的数据维度 [batch ,in_height,in_wight,in_channels]
卷积核的维度是 [filter_height,filter_heught,in_channel,channel_multiplierl]
将不同的卷积和独立的应用在in_channels 的每一个通道上(从通道 1 到通道channel_multiplier)
然后将所有结果进行汇总,输出通道的总数是,in_channel * channel_multiplier

代码如下

input_data = tf.Variable(np.random.rand(10, 9, 9, 3), dtype=np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 2), dtype=np.float32)

y = tf.nn.depthwise_conv2d(input_data, filter_data, strides=[1, 1, 1, 1], padding='SAME')
print('tf.nn.depthwise_conv2d : ', y)

# tf.nn.depthwise_conv2d :  Tensor("depthwise:0", shape=(10, 9, 9, 6), dtype=float32)
# 输出的通道数增加了

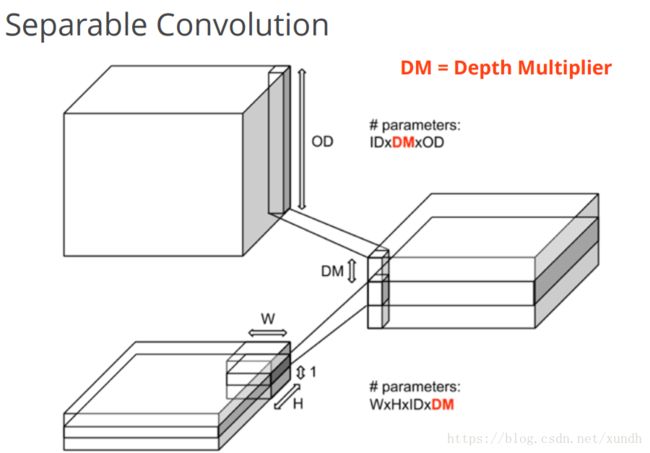
tf.nn.separable_conv2d

是利用几个分离的卷积核去做卷积。首先用depthwise_filter做卷积，效果与depthwise_conv2d相同，然后用1x1的卷积核pointwise_filter去做卷积。

使用卷积函数对图像感兴趣的区域进行批注

图像感兴趣区域是指图像内部的一个子区域由计算机自动进行标注的方式。在实际使用中常用不同的卷积核进行。
代码：

import tensorflow as tf
import cv2
import numpy as np

img = cv2.imread("lena.jpg")
img = np.array(img, dtype=np.float32)
x_image = tf.reshape(img, [1, 512, 512, 3])

filter = tf.Variable(tf.ones([7, 7, 3, 1]))
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    res = tf.nn.conv2d(x_image, filter, strides=[1, 2, 2, 1], padding='SAME')
    res_image = sess.run(tf.reshape(res, [256, 256])) / 128+1
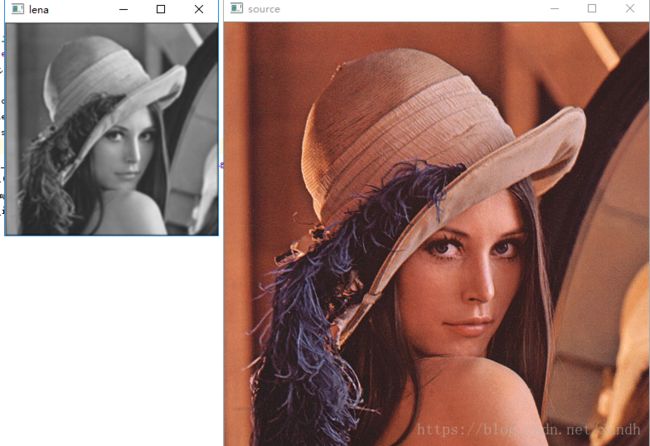
cv2.imshow('source', img.astype('uint8'))
cv2.imshow("lena", res_image.astype('uint8'))
cv2.waitKey()

运行效果：

换个图片的效果：

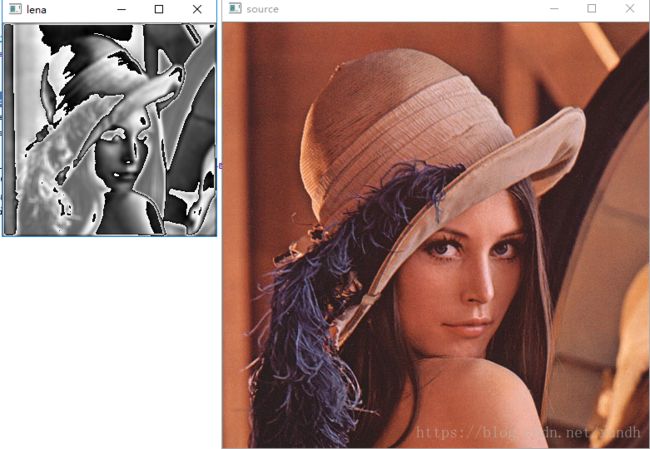
卷积核改为[11,11]效果：

filter = tf.Variable(tf.ones([11, 11, 3, 1]))

下一篇学习池化运算。

本文部分内容来源于：
https://blog.csdn.net/fontthrone/article/details/76652753
https://www.cnblogs.com/hans209/p/7103168.html