二叉树-详解二叉排序树

篇一：二叉树-遍历终极版
篇二：二叉树-创建、重建、转化
篇三：二叉树-详解二叉排序树
篇四：二叉树-详解平衡二叉树AVL
篇五：二叉树-常见简单算法题

二叉搜索树

首先二叉排序树也是一棵二叉树，所谓二叉树，就是“任何节点最多只允许两个子节点”，这两个子节点称为左右子节点。如下便是一个二叉树。

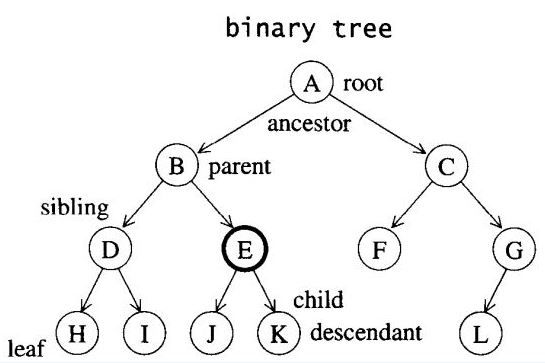
1、二叉排序树性质：

1、就是若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2、若它的右子树不空，则右子树上所有节点的值均大于其根节点的值。
3、换句话说就是：任何节点的键值一定大于其左子树中的每一个节点的键值，并小于其右子树中的每一个节点的键值。
如下便是一颗二叉排序树：

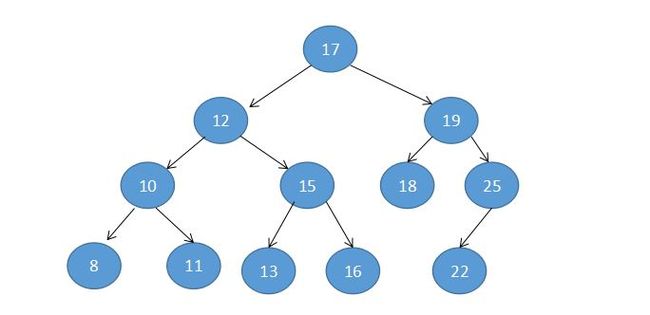
定义一个二叉排序树结构：

typedef int DataType;
typedef struct BST_Node {
    DataType data;
    struct BST_Node *lchild, *rchild;
}BST_T, *BST_P;

建立二叉排序树，用到Insert_BST方法，在后面：

void CreateBST(BST_P *T, int a[], int n)
{
    int i;
    for (i = 0; i < n; i++)
    {
        Insert_BST(T, a[i]);
    }
}

2、二叉排序树查找

要在二叉树中找出查找最大最小元素是极简单的事情，从根节点一直往左走，直到无路可走就可得到最小值；从根节点一直往右走，直到无路可走，就可以得到最大值。

查找最小关键字：

BST_P SearchMin(BST_P root)
{
    if (root == NULL)
        return NULL;
    if (root->lchild == NULL)
        return root;
    else  //一直往左孩子找，直到没有左孩子的结点  
        return SearchMin(root->lchild);
}

查找最大关键字：

BST_P SearchMax(BST_P root)
{
    if (root == NULL)
        return NULL;
    if (root->rchild == NULL)
        return root;
    else  //一直往右孩子找，直到没有右孩子的结点  
        return SearchMax(root->rchild);
}

二叉排序树查找单个元素也比较方便。

递归版查找（找到返回关键字的结点指针，没找到返回NULL）：

BST_P Search_BST(BST_P root, DataType key)
{
    if (root == NULL)
        return NULL;
    if (key > root->data) //查找右子树  
        return Search_BST(root->rchild, key);
    else if (key < root->data) //查找左子树  
        return Search_BST(root->lchild, key);
    else
        return root;
}

非递归版查找：

BST_P Search_BST(BST_P root, DataType key)
{
    BST_P p = root;
    while (p) 
    {       
        if (p->data == key)  return p;
        p = (key < p->data) ? p->lchild : p->rchild;
    }
    return NULL;
}

3、二叉排序树插入

插入新元素时，可以从根节点开始，遇键值较大者就向左，遇键值较小者就向右，一直到末端，就是插入点。

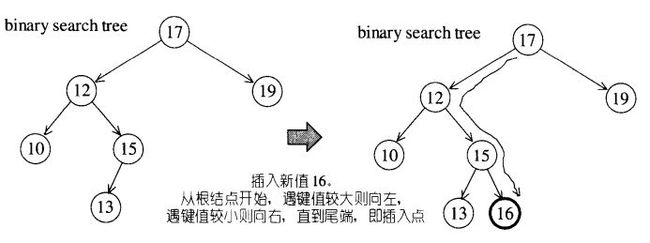
插入代码如下：

void Insert_BST(BST_P *root, DataType data)
{
    //初始化插入节点
    BST_P p = (BST_P)malloc(sizeof(struct BST_Node));
    if (!p) return;
    p->data = data;
    p->lchild = p->rchild = NULL;

    //空树时，直接作为根节点
    if (*root == NULL)
    {
        *root = p;
        return;
    }

    //是否存在，已存在则返回，不插入
    if (Search_BST(root, data) != NULL) return; 

    //进行插入，首先找到要插入的位置的父节点
    BST_P tnode = NULL, troot = *root;
    while (troot)
    {       
        tnode = troot;
        troot = (data < troot->data) ? troot->lchild : troot->rchild;
    }
    if (data < tnode->data)
        tnode->lchild = p;
    else
        tnode->rchild = p;
}

4、二叉排序树删除

对于二叉排序树中的节点A，对它的删除分为两种情况：
1、如果A只有一个子节点，就直接将A的子节点连至A的父节点上，并将A删除；

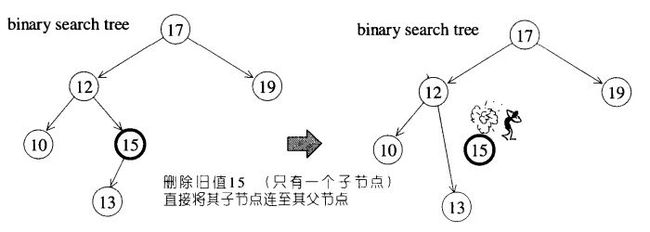
2、如果A有两个子节点，我们就以右子树内的最小节点取代A，怎么得最小节点，前有有说。



删除节点代码：

void DeleteBSTNode(BST_P *root, DataType data)
{
    BST_P p = *root, parent = NULL, s = NULL;

    if (!p) return;

    if (p->data == data) //找到要删除的节点了
    {
        /* It's a leaf node */
        if (!p->rchild && !p->lchild) 
            *root = NULL;

        // 只有一个左节点
        else if (!p->rchild&&p->lchild) 
            *root = p->lchild;

        // 只有一个右节点
        else if (!p->lchild&&p->rchild) 
            *root = p->rchild;

        //左右节点都不空
        else 
        {
            s = p->rchild;
            /* the s without left child */
            if (!s->lchild)
                s->lchild = p->lchild;
            /* the s have left child */
            else 
            {
                /* find the smallest node in the left subtree of s */
                while (s->lchild) 
                {
                    /* record the parent node of s */
                    parent = s;
                    s = s->lchild;
                }
                parent->lchild = s->rchild;
                s->lchild = p->lchild;
                s->rchild = p->rchild;
            }
            *root = s;
        }
        free(p);
    }
    else if (data > p->data) //向右找
        DeleteBSTNode(&(p->rchild), data);
    else if (data < p->data) //向左找
        DeleteBSTNode(&(p->lchild), data);
}

5、二叉排序树遍历

为了查看二叉排序树的情况，我们给出遍历代码，这里不重点讲解遍历，就只贴个递归版的遍历，这个简单：
1、先序遍历

void PreOrderTraverse(BST_P T)
{
    if (T)
    {
        cout << T->data << " ";
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

2、中序遍历

void MidOrderTraverse(BST_P T)
{
    if (T)
    {
        MidOrderTraverse(T->lchild);
        cout << T->data << " ";
        MidOrderTraverse(T->rchild);
    }
}

3、后序遍历

void PostOrderTraverse(BST_P T)
{
    if (T)
    {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        cout << T->data << " ";
    }
}

6、二叉排序树测试

测试代码如下：

int main()
{
    int arr[] = { 17,12,19,10,15,18,25,8,11,13,16,22};  

    BST_P root = NULL;

    //创建二叉排序树
    CreateBST(&root, arr, 12);
    printf("\nCreate BST: ");
    printf("\npre order traverse: ");
    PreOrderTraverse(root);
    printf("\npost order traverse: ");
    PostOrderTraverse(root);
    cout << endl;

    //在二叉排序树中查找节点12.
    BST_P result = Search_BST(root, 12);
    printf("\nSearch Data: ");
    cout << "查找结果：\n" << "指针：" << result << endl << "指针的值：" << result->data << endl;

    //在二叉排序树中插入9
    Insert_BST(&root, 9);
    printf("\nInsert Data: ");
    printf("\npre order traverse: ");
    PreOrderTraverse(root);
    printf("\npost order traverse: ");
    PostOrderTraverse(root);
    cout << endl;

    //删除二叉排序树中的节点12
    DeleteBSTNode(&root, 12);
    printf("\nDelete Data: ");
    printf("\npre order traverse: ");
    PreOrderTraverse(root);
    printf("\npost order traverse: ");
    PostOrderTraverse(root);
    printf("\n");
}

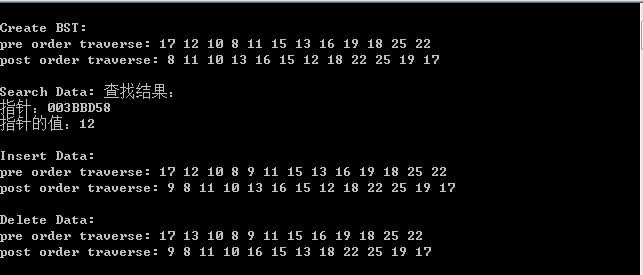
测试结果如下：

参考资料

1、STL源码解析；
2、博客：http://blog.csdn.net/xiajun07061225/article/details/8292505