一个简单的案例带你了解支持向量机算法(Python代码)
介绍
掌握机器学习算法并不是一个不可能完成的事情。大多数的初学者都是从学习回归开始的。是因为回归易于学习和使用,但这能够解决我们全部的问题吗?当然不行!因为,你要学习的机器学习算法不仅仅只有回归!
把机器学习算法想象成一个装有斧头,剑,刀,弓箭,匕首等等武器的军械库。你有各种各样的工具,但你应该学会在正确的时间和场合使用它们。作为一个类比,我们可以将“回归”想象成一把能够有效切割数据的剑,但它无法处理高度复杂的数据。相反,“支持向量机”就像一把锋利的刀—它适用于较小的数据集,但它可以再这些小的数据集上面构建更加强大的模型。
现在,我希望你现在已经掌握了随机森林,朴素贝叶斯算法和模型融合的算法基础。如果没有,我希望你先抽出一部分时间来了解一下他们,因为在本文中,我将指导你了解认识机器学习算法中关键的高级算法,也就是支持向量机的基础知识。
如果你是初学者,并且希望开始你的数据科学之旅,那么我希望你先去了解一些基础的机器学习算法, 支持向量机相对来说对于数据科学的初学者来讲的确有一点难了。
0.什么是分类分析
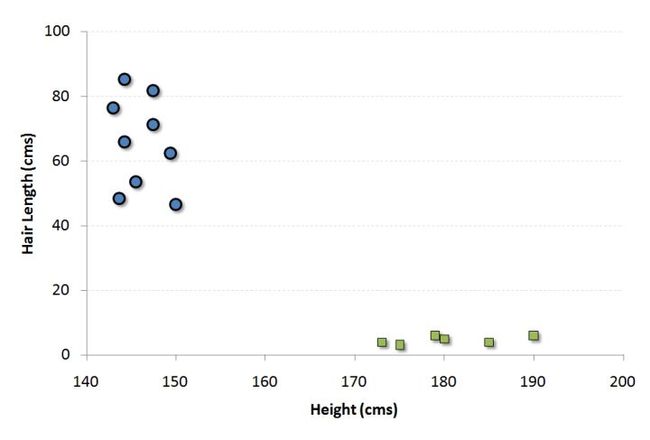
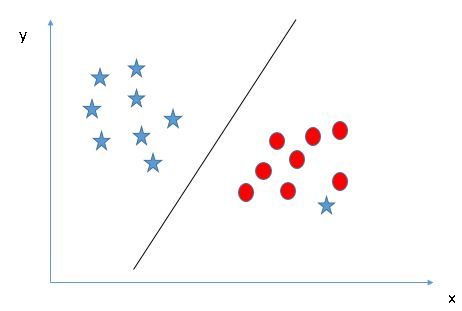
让我们用一个例子来理解这个概念。假如我们的人口是按照50%-50%分布的男性和女性。那么使用这个群体的样本,就需要创建一些规则,这些规则将指导我们将其他人的性别进行分类。如果使用这种算法,我们打算建立一个机器人,可以识别一个人是男性还是女性。这是分类分析的样本问题。我们将尝试使用一些规则来划分性别之间的不同。为简单起见,我们假设使用的两个区别因素是:个体的身高和头发长度。以下是样本的散点图。
图中的蓝色圆圈表示女性,绿色方块表示男性。图中的一些预期见解是:
我们人口中的男性的平均身高较高。
我们人口中的女性的头发较长。
如果我们看到一个身高180厘米,头发长度为4厘米的人,我们最好的分类是将这个人归类为男性。这就是我们进行分类分析的方法。
1.什么是支持向量机
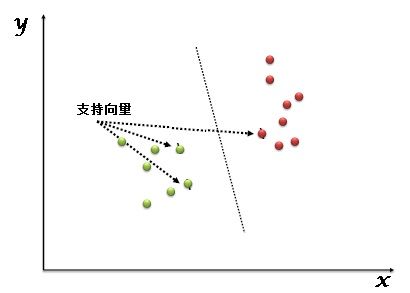
“支持向量机”(SVM)是一种有监督的机器学习算法,可用于分类任务或回归任务。但是,它主要适用于分类问题。在这个算法中,我们将每个数据项绘制为n维空间中的一个点(其中n是你拥有的是特征的数量),每个特征的值是特定坐标的值。然后,我们通过找到很好地区分这两个类的超平面来执行分类的任务(请看下面的演示图片)。
支持向量只是个体观测的坐标。支持向量机是一个最好地隔离两个类(超平面或者说分类线)的前沿算法。
在我第一次听到“支持向量机”这个名字,我觉得这个名字听起来好复杂,如果连名字都这么复杂的话,那么这个名字的概念将超出我的理解。幸运的是,在我看了一些大学的讲座视频,才意识到这个算法其实也没有那么复杂。接下来,我们将讨论支持向量机如何工作。我们将详细探讨该技术,并分析这些技术为什么比其他技术更强。
2.它是如何工作的?
上面,我们已经习惯了用超平面来隔离两种类别的过程,但是现在最迫切的问题是“我们如何识别正确的超平面?”。关于这个问题不用急躁,因为它并不像你想象的那么难!
让我们一个个的来理解如何识别正确的超平面:
- 选择正确的超平面(场景1):这里,我们有三个超平面(A、B、C)。现在,让我们用正确的超平面对星形和圆形进行分类。
你需要记住一个经验的法则来识别正确的超平面:“选择更好的可以隔离两个类别的超平面”。在这种情况下,超平面“B”就非常完美的完成了这项工作。
- 选择正确的超平面(场景2):
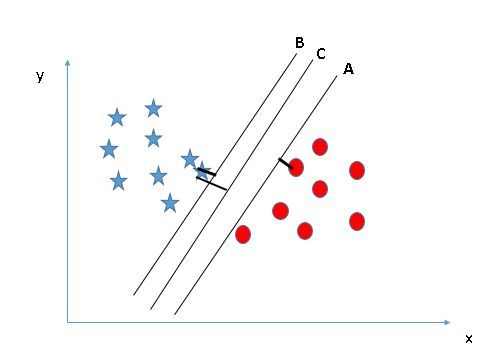
- 在这里,我们有三个超平面(A,B,C),并且所有这些超平面都很好地隔离了类。现在,我们如何选择正确的超平面?
- 在这里,在这里,将最近的数据点(任一类)和超平面之间的距离最大化将有
- 助于我们选择正确的超平面。该距离称为边距。让我们看一下下面的图片:
上面,你可以看到超平面C的边距与A和B相比都很高。因此,我们将正确的超平面选择为C。选择边距较高的超平面的另一个决定性因素是稳健性。如果我们选择一个低边距的超平面,那么很有可能进行错误分类。
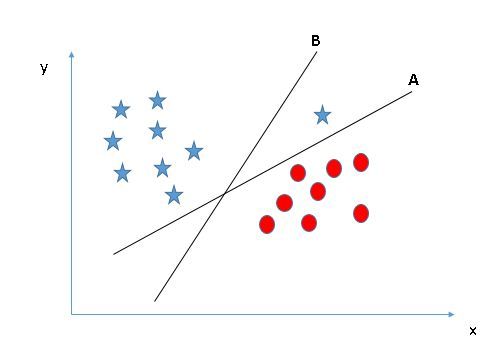
- 选择正确的超平面(场景3):提示: 使用我们前面讨论的规则来选择正确的超平面
你们中的一些人可能选择了超平面B,因为它与A相比具有更高的边距。但是SVM选择超平面是需要在最大化边距之前准确地对类别进行分类。这里,超平面B有一个分类的错误,而且A进行了正确的分类。因此,正确的超平面应该是A.
- 我们可以对这个两个类进行分类吗?(场景4):下面这张图片中,我们无法使用直线来分隔这两个类,因为其中一个星星位于圆形类别的区域中作为一个异常值。
正如我刚刚已经提到的,另一端的那一颗星星就像是一个异常值。SVM具有忽略异常值并找到具有最大边距的超平面的功能。因此,我们可以说,SVM对异常值有很强的稳健性
- 找到一个超平面用来隔离两个类别(场景5):
- 在下面的场景中,我们不能在两个类之间有线性的超平面,那么SVM如何对这两个类进行分类?到目前为止,我们只研究过线性超平面。
SVM可以解决这个问题。并且是轻松就可以做到!它通过引入额外的特征来解决这个问题。在这里,我们将添加一个新特征
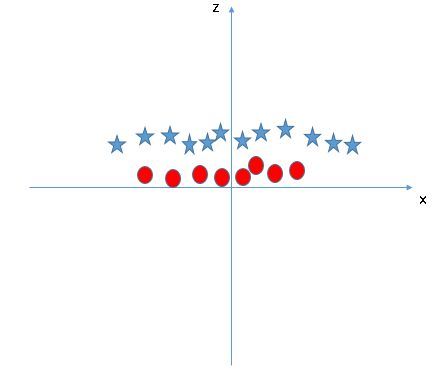
现在,让我们绘制轴x和z上的数据点:
在上图中,要考虑的问题是:
- z的所有值都是正的,因为z是x和y的平方和
- 在原图中,红色圆圈出现在靠近x和y轴原点的位置,导致z值比较低。星形相对远离原点,导致z值较高。
在SVM中,很容易就可以在这两个类之间建立线性超平面。但是,另一个需要解决的问题是,我们是否需要手动添加一个特征以获得超平面。不,并不需要这么做,SVM有一种称为核技巧的技术。这些函数把低维度的输入空间转换为更高维度的空间,也就是它将不可分离的问题转换为可分离的问题,这些函数称为内核函数。它主要用于非线性的分离问题。简而言之,它执行一些非常复杂的数据转换,然后根据你定义的标签或输出找出分离数据的过程。
当SVM找到一条合适的超平面之后,我们在原始输入空间中查看超平面时,它看起来像一个圆圈:
现在,让我们看看在数据科学中应用SVM算法的方法。
3.如何在Python中实现SVM?
在Python中,scikit-learn是一个广泛使用的用于实现机器学习算法的库,SVM也可在scikit-learn库中使用并且遵循相同的结构(导入库,创建对象,拟合模型和预测)。我们来看下面的代码:
导入库
from sklearn import svm
假设您有用于训练数据集的X(特征数据)和Y(目标),以及测试数据的x_test(特征数据)
创建SVM分类对象
model = svm.svc(kernel='linear', c=1, gamma=1)
与之相关的选项有很多,比如更改kernel值(内核)、gamma值和C值。下一节将对此进行更多讨论。使用训练集训练模型,并检查成绩
model.fit(X, y)
model.score(X, y)
预测输出
predicted= model.predict(x_test)
4.如何调整SVM的参数?
对机器学习算法进行调整参数值可以有效地提高模型的性能。让我们看一下SVM可用的参数列表。
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma=0.0, coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, random_state=None)
下面将讨论一些对模型性能影响较大的重要参数,如“kernel”,“gamma”和“C”。
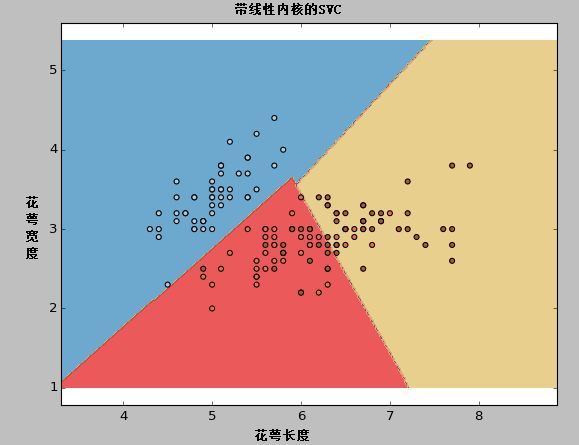
kernel:我们之间已经简单的讨论过了。在算法参数中,我们可以为kernel值提供各种内核选项,如“linear”,“rbf”,“poly”等(默认值为“rbf”)。其中“rbf”和“poly”对于找到非线性超平面是很有用的。让我们看一下这个例子,我们使用线性内核函数对iris数据集中的两个特性进行分类。
示例:使用linear的内核
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
导入数据
iris = datasets.load_iris()
X = iris.data[:, :2] #我们可以只考虑前两个特征
我们可以使用双数据集来避免丑陋的切片
y = iris.target
我们创建了一个SVM实例并对数据进行拟合。不进行缩放
是因为我们想要画出支持向量
C = 1.0 #SVM正则化参数
svc = svm.SVC(kernel='linear', C=1,gamma=0).fit(X, y)
创建一个网格来进行可视化
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
plt.subplot(1, 1, 1)
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
plt.show()
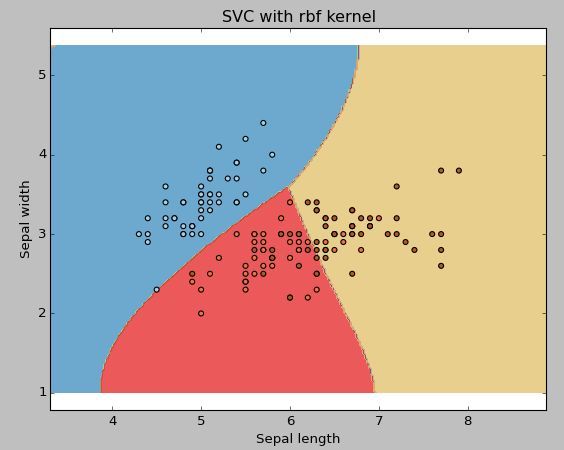
示例:使用RBF内核
将内核类型更改为下面的代码行中的rbf并查看影响。
svc = svm.SVC(kernel ='rbf',C = 1,gamma = 0).fit(X,y)
](
如果你有大量的特征数据(> 1000),那么我建议你去使用线性内核,因为数据在高维空间中更可能是线性可分的。此外,你也可以使用RBF,但不要忘记交叉验证其参数,以避免过度拟合。
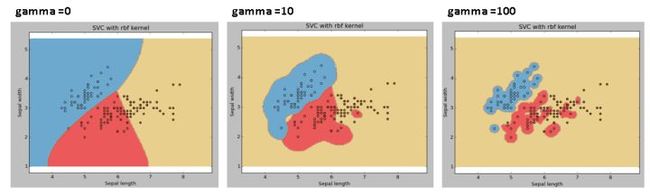
gamma:'rbf','poly'和'sigmoid'的内核系数。伽马值越高,则会根据训练数据集进行精确拟合,也就是泛化误差从而导致过拟合问题。
示例:如果我们使用不同的伽玛值,如0,10或100,让我们来查看一下不同的区别。
svc = svm.SVC(kernel ='rbf',C = 1,gamma = 0).fit(X,y)
C:误差项的惩罚参数C. 它还控制了平滑决策边界与正确分类训练点之间的权衡。
我们应该始终关注交叉验证的分数,以便更有效地组合这些参数并避免过度拟合。
5.SVM的优缺点
优点:
它工作的效果很明显,有很好的分类作用
它在高维空间中同样是有效的。
它在尺寸数量大于样本数量的情况下,也是有效的。
它在决策函数(称为支持向量)中使用训练点的子集,因此它的内存也是有效的
缺点:
当我们拥有大量的数据集时,它表现并不好,因为它所需要的训练时间更长
当数据集具有很多噪声,也就是目标类重叠时,它的表现性能也不是很好
SVM不直接提供概率估计,这些是使用昂贵的五重交叉验证来计算的。它是Python scikit-learn库的相关SVC方法。
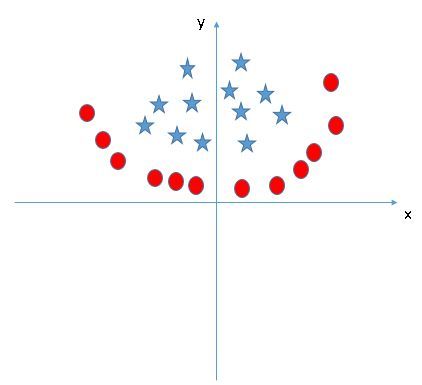
实践问题
找到一个正确的超平面用来将下面图片中的两个类别进行分类
结语
在本文中,我们详细介绍了机器学习算法中的高阶算法,支持向量机(SVM)。我们讨论了它的工作原理,python中的实现过程,通过调整模型的参数来提高模型效率的技巧,讨论了SVM的优缺点,以及最后留下的一个要你们自己解决的问题。我建议你使用SVM并通过调整参数来分析此模型的能力。
支持向量机是一种非常强大的分类算法。当与随机森林和其他机器学习工具结合使用时,它们为集合模型提供了非常不同的维度。因此,在需要非常高的预测能力的情况下,他们就显得非常重要。由于公式的复杂性,这些算法可能稍微有些难以可视化。
Understanding Support Vector Machine algorithm from examples (along with code)
更多精彩内容,可移步:https://www.cda.cn/?seo-jianshu