手把手教你实现一个向量
文章目录
- 什么是向量
- 向量提供哪些接口
- 实现
- 宏定义
- 定义类
- 成员变量
- 构造函数与析构函数
- 构造函数
- 析构函数
- 成员函数
- size()
- get(r)
- put(r, e)
- expand()
- insert(r, e)
- remove(lo, hi)
- remove(r)
- disordered()
- sort(lo, hi)
- find(e, lo, hi)
- search(e, lo, hi)
- deduplicate()
- uniquify()
- 重载 “[]” 运算符
- 结语
什么是向量
对于向量的解释网上已经有很多,我这里就不再赘述,简单来说就是一个加强版的数组,在Java中,向量有另外一个名字——数组列表(ArrayList),向量提供了一些接口,使我们可以很方便地对数组中的元素进行一些操作。如果有读者实在不明白向量的含义,可以读一下下面这段话,知道什么是向量的读者,可以直接跳过。
对数组结构进行抽象与扩展之后,就可以得到向量结构,因此向量也称作数组列表(Array list)。向量提供一些访问方法,使得我们可以通过下标直接访问序列中的元素,也可以将指定下标处的元素删除,或将新元素插入至指定下标。为了与通常数组结构的下标(Index)概念区分开来,我们通常将序列的下标称为秩(Rank)。
假定集合 S 由n 个元素组成,它们按照线性次序存放,于是我们就可以直接访问其中的第一个元素、第二个元素、第三个元素……。也就是说,通过[0, n-1]之间的每一个整数,都可以直接访问到唯一的元素e,而这个整数就等于S 中位于e 之前的元素个数——在此,我们称之为该元素的秩(Rank)。不难看出,若元素e 的秩为r,则只要e 的直接前驱(或直接后继)存在,其秩就是r-1(或r+1)。
支持通过秩直接访问其中元素的序列,称作向量(Vector)或数组列表(Array list)。实际上,秩这一直观概念的功能非常强大——它可以直接指定插入或删除元素的位置。
摘自:简书 作者:峰峰小 链接:https://www.jianshu.com/p/c653a93409b0
向量中有几个常用的概念,这里有必要介绍一下,因为在代码注释中会用到。
- 规模。向量的规模指的是向量中元素的个数。
- 容量。容量指的是向量可容纳的元素的个数。
- 秩。向量的秩本质上就是数组的下标,在访问向量的元素时,我们是通过秩来访问的。长度为n的数组的下标范围是0n-1,那么对应的,规模为n的向量的秩的范围也是0n-1。一般用字母r来表示秩。
- 区间。向量的区间指的是向量中某一段连续的元素序列,一般遵循左闭右开的原则,也就是说如果我们想表示向量 v 的从第2个元素到第5个元素这段区间,我们会写成 v[2, 6),即使 v[6] 是一个不存在的元素。相应的,我们在给函数传参时,如果涉及到区间,也会遵循这个原则。比如下面要讲到的向量类的构造函数,如果用一个数组 A 的第2个元素到第5个元素去初始化一个向量,我们给构造函数传参的形式是:
Vector(A, 2, 6)。注意到了吗?我们给给构造函数传的右边界的值是「6」,而不是「5」。再比如,如果想对向量 v 的第2个元素到第5个元素进行排序,我们应该这样写:v.sort(2, 6)。这就是区间的表达方式。
向量提供哪些接口
| 操作 | 功能 | 适用对象 |
|---|---|---|
| size() | 报告当前向量的规模(元素总数) | 向量 |
| get® | 获取秩为r的元素 | 向量 |
| put(r, e) | 用e替换秩为r的元素的数值 | 向量 |
| expand() | 向量空间不足时扩容,将向量的容量扩大为原来的 2 倍 | 向量 |
| insert(r, e) | e作为秩为r的元素插入,原后继元素依次后移 | 向量 |
| remove(lo, hi) | 删除区间[lo, hi)内的元素,该区间的后继元素整体前移 hi-lo 个单位 | 向量 |
| remove® | 删除秩为r的元素,返回该元素中原存放的对象 | 向量 |
| disordered() | 判断所有元素是否已按非降序排列 | 向量 |
| sort() | 调整各元素的位置,使之按非降序排列 | 向量 |
| find(e, lo, hi) | 在区间[lo, hi)内查找目标元素e | 向量 |
| search(e, lo, hi) | 在区间[lo, hi)内查找目标元素e,返回不大于e且秩最大的元素的秩 | 有序向量 |
| deduplicate() | 剔除重复元素 | 向量 |
| uniquify() | 剔除重复元素 | 有序向量 |
实现
本文中的向量实现代码用C++编写,代码运行环境为Visual Studio 2017 Community。
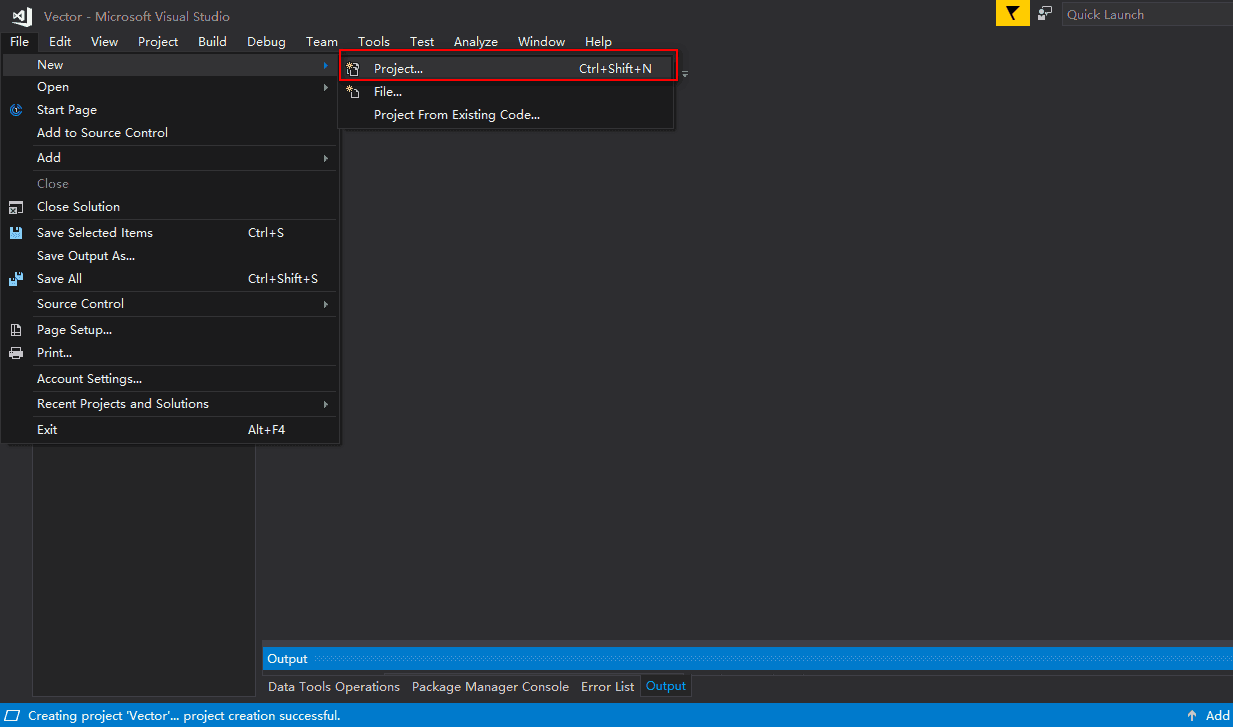
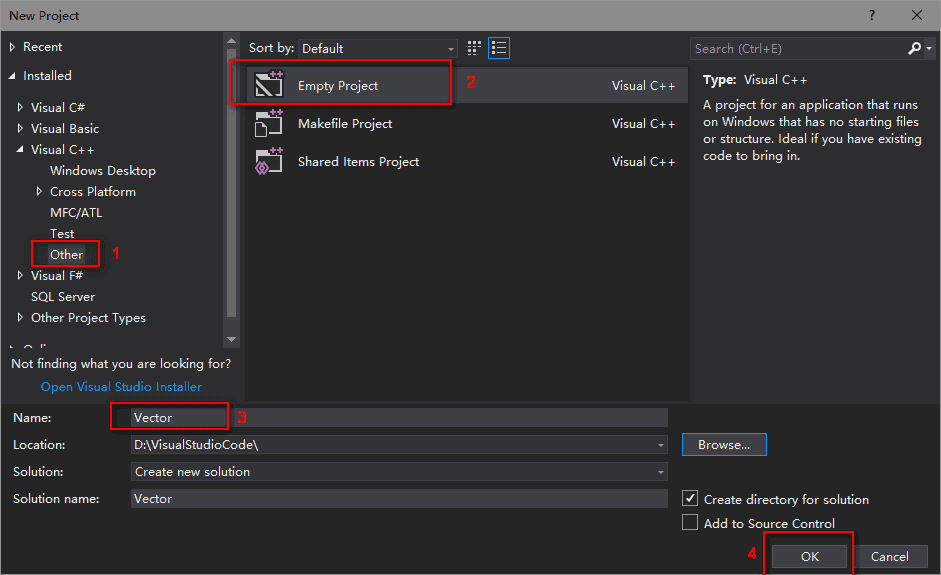
在VS中新建一个项目,点击 File -> New -> Project,为新项目取名为Vector。如下图所示:
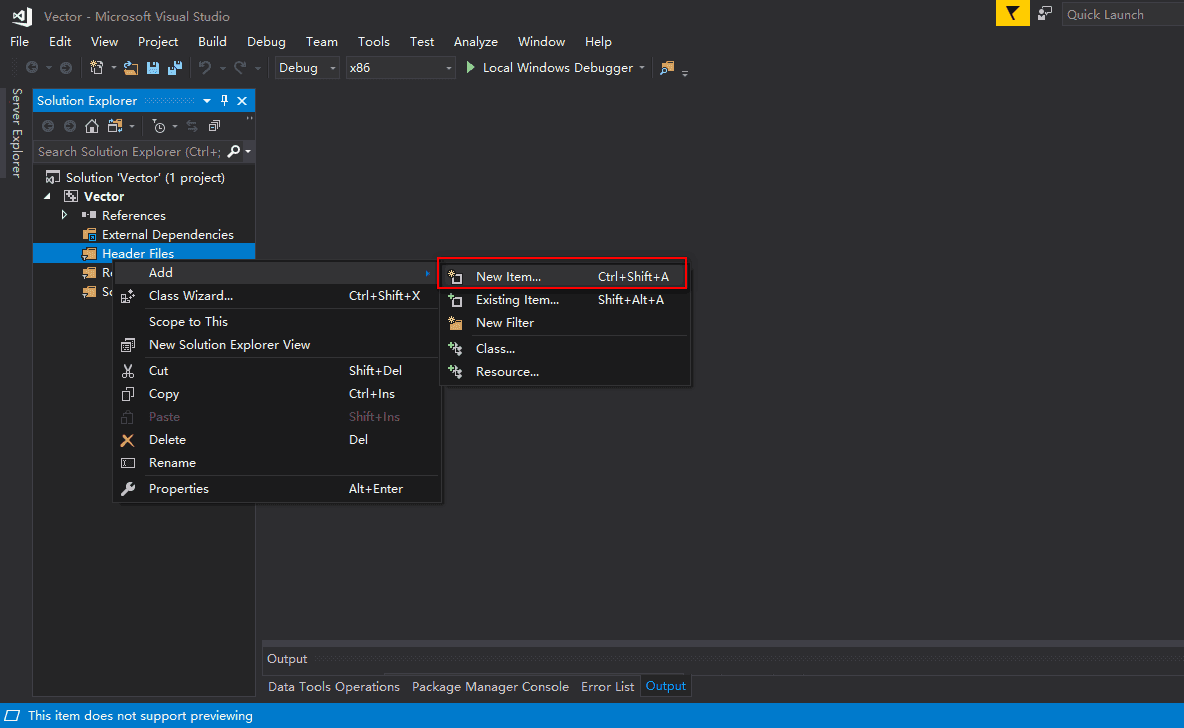
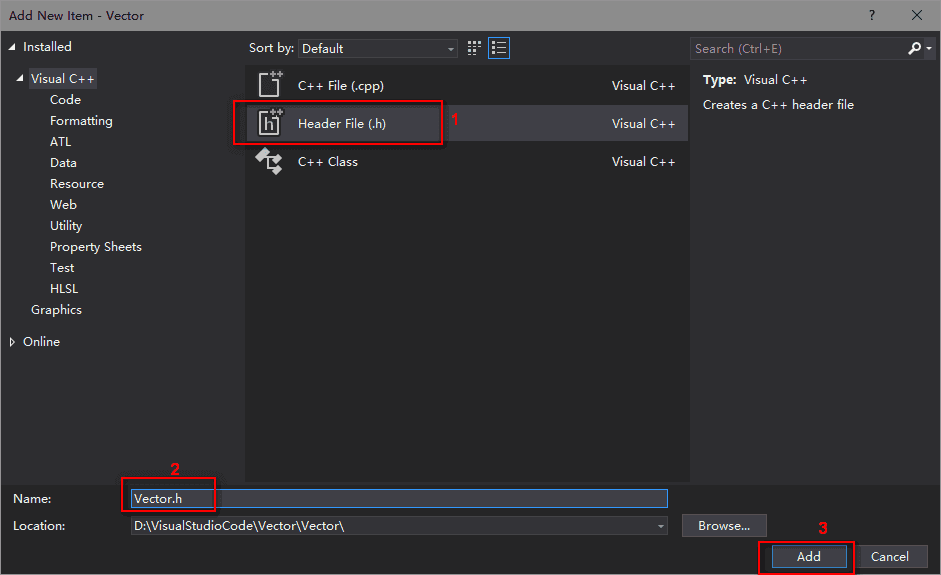
右击项目文件夹Header Files -> Add -> New Item,新建一个头文件,取名为Vector.h,如下图所示:
宏定义
typedef int Rank; //秩
#define DEFAULT_CAPACITY 3 //默认初始容量(实际应用中可设置为更大);
定义类
定义向量类Vector
template <typename T> class Vector{ //向量模板类
};
T是一个泛型类型,代表要放进向量的数据的类型。
成员变量
向量类有三个属性:规模、容量、数据区的首地址。在代码中分别定义如下:
private:
Rank _size; //规模
int _capacity; //容量
T* _elem; //数据区
我们在私有变量前面加了一个下划线,用来区分它们和普通变量的区别,希望读者朋友们也能养成这样一个良好的命名习惯。
此时Vector.h文件的内容应该如下图所示:
构造函数与析构函数
构造函数
所谓构造函数,就是告诉机器,在我声明一个向量的对象时,你应该做什么。这里我们重载了4个构造函数,分别应用于不同的场景。
- 默认的构造函数。
Vector(int c = DEFAULT_CAPACITY),函数返回一个容量为 c 的向量对象。 - 数组区间复制。
Vector(T const * A, Rank lo, Rank hi),函数返回一个容量为 hi-lo 的向量对象,且向量对象的第一个元素到最后一个元素分别等于A[lo] ~ A[hi-1]。 - 向量区间复制。
Vector(Vector,函数返回一个容量为 hi-lo 的向量对象,且向量对象的第一个元素到最后一个元素分别等于const& V, Rank lo, Rank hi) V[lo] ~ V[hi-1]。 - 向量整体复制。
Vector(Vector,函数返回一个和向量 V 一模一样的向量对象。const& V)
有读者可能会问,为什么不能用「数组整体复制」的方式来初始化一个向量呢?类似于这样:Vector(T const * A)?因为数组本身没有长度这个属性,如果只传一个数组给函数,那么在函数内部无法确定数组的长度,那么也就无法确定即将初始化的向量的长度了。如果想用一整个数组来初始化向量,假设数组长度为n,那么你可以这样做:Vector(A, 0, n)。
好了,接下来我们看一下构造函数具体的实现方式。不过,在这之前,我还要说一件事(读者大大们不要嫌我啰嗦)。不知道大家发现了没有,除了第一个构造函数,其余的3个构造函数都有一个相同的操作,那就是复制。因为我们说了,向量的底层也是数组,所以,抽象出来看,这三个构造函数其实都是把一个数组的某一段区间元素复制到另一个数组上去。那么我们可以写一个执行复制操作的函数,让这三个构造函数在初始化向量时都调用这一个函数就可以了,只不过传的参数不一样。来看一下具体代码:
/* T为基本类型或已重载赋值操作符“=”。复制内容为A[lo]至A[hi-1]*/
void copyFrom(T const *A, Rank lo, Rank hi) {
_elem = new T[_capacity = 2 * (hi - lo)]; //分配空间
_size = 0; //规模清零
while (lo < hi) { //A[lo, hi)内的元素逐一
_elem[_size++] = A[lo++]; //复制至_elem[0, hi-lo]
}
}
下面是构造函数的代码实现:
/* 默认的构造函数 */
Vector(int c) {
_elem = new T[_capacity = c];
_size = 0;
}
/* 数组区间复制 */
Vector(T const *A, Rank lo, Rank hi) {
copyFrom(A, lo, hi);
}
/* 向量区间复制 */
Vector(Vector<T> const& V, Rank lo, Rank hi) {
copyFrom(V._elem, lo, hi);
}
/* 向量整体复制 */
Vector(Vector<T> const& V) {
copyFrom(V._elem, 0, V._size);
}
此时 Vector.h 的代码结构应该是这样的:
析构函数
析构函数正好和构造函数相反,析构函数是告诉计算机,在一个向量的对象被销毁时,你应该做什么。当一个向量被销毁时,应该释放它所占用的内存空间,这样才不会导致内存泄漏。下面是析构函数的实现代码:
/* 析构函数,释放内部空间 */
~Vector(){
delete [] _elem;
}
成员函数
接下来所要实现的成员函数都是公有的。
size()
这个函数的返回值是一个非负整数,返回的是当前向量的规模,适用对象是所有的向量。
int size()
{
return _size;
}
get®
获取秩为r的元素,返回值类型是T,适用对象是所有的向量。
//获取秩为r的元素
T get(Rank r) {
return _elem[r];
}
put(r, e)
用e替换秩为r的元素的数值,若 r 是一个合法的值,则返回 r,否则,返回 -1。要求向量中的元素是基本类型或已经重载运算符 “=”。
//用e替换秩为r的元素的数值
Rank put(r, e) {
if (0 <= r < _size) { //判断秩r是否合理
_elem[r] = e;
return r;
}
else return -1; //如果r不合理,返回-1
}
expand()
向量空间不足时扩容,将向量的容量扩大为原来的 2 倍。要求向量中的元素是基本类型或已经重载运算符 “=”。
/* 向量空间不足时扩容 */
void expand(){
if(_size < _capacity) //尚未满员时,不必扩容
return;
_capacity = max(_capacity, DEFAULT_CAPACITY); //不低于最小容量
T* oldElem = _elem;
_elem = new T[_capacity <<= 1]; //容量加倍
for (int i = 0; i < _size; i++)//复制原向量内容
_elem[i] = oldElem[i]; //T为基本类型,或已重载运算符“=”
delete [] oldElem; //释放原空间
}
insert(r, e)
e作为秩为r的元素插入,原后继元素依次后移,函数返回值是新插入的元素的秩。要求向量中的元素是基本类型或已经重载运算符 “=”。
/* 将元素e插入到秩为r的位置,0 <= r <= size */
Rank insert(Rank r, T const & e) {//O(n-r)
expand(); //若有必要,扩容
for (int i = _size; i > r; i--) { //自后向前
_elem[i] = _elem[i - 1]; //后继元素顺次后移一个单元
}
_elem[r] = e;
_size++; //置入新元素,更新容量
return r; //返回秩
}
remove(lo, hi)
多元素删除。删除区间[lo, hi)内的元素,该区间的后继元素整体前移 hi-lo 个单位,返回被删除元素的数目。适用对象是所有的向量。要求向量中的元素是基本类型或已经重载运算符 “=”。
/* 删除区间[lo, hi), 0 <= lo <= hi <= size */
int remove(Rank lo, Rank hi){ //O(n - hi)
if(lo == hi) //出于效率考虑,单独处理退化情况
return 0;
while (hi < _size) //[hi, _size)顺次前移hi-lo位
_elem[lo++] = _elem[hi++];
_size = lo; //更新规模,若有必要则缩容
return hi - lo; //返回被删除元素的数目
}
remove®
单元素删除。删除秩为r的元素,返回该元素中原存放的对象。适用对象是所有的向量。
/* 单元素删除
* 可以视作区间删除操作的特例:[r] = [r, r + 1) */
T remove(Rank r){
T e = _elem[r]; //备份被删除的元素
remove(r, r + 1); //调用区间删除算法
return e; //返回被删除的元素
}
disordered()
判断所有元素是否已按非降序排列,返回值是逆序对的个数,若返回 0,则表示元素已经是非降序排列。适用对象是所有的向量。要求向量中的元素是基本类型或已经重载运算符 “>”。
int disordered() const {
int n = 0; //计数器
for (int i = 1; i < _size; i++) //逐一检查各对相邻元素
n += (_elem[i - 1] > _elem[i]); //逆序则计数
return n; //返回值n是向量中逆序对的个数,当且仅当 n = 0 时向量有序
}//若只需判断是否有序,则首次遇到逆序对之后,即可立即终止
sort(lo, hi)
调整各元素的位置,使之按非降序排列。这里采用的是归并排序。适用对象是所有的向量。要求向量中的元素是基本类型或已经重载运算符 “<”、“=”。算法的原理我之前的一篇文章中提到过,这里不再赘述。感兴趣的读者可以戳这里,归并排序
。
void sort(Rank lo, Rank hi){
mergeSort(Rank lo, Rank hi);
}
void mergeSort(Rank low, Rank high)
{
Rank step = 1;
while (step < high) {
for (Rank i = low; i < high; i += step << 1) {
Rank lo = i, hi = (i + (step << 1)) <= high ? (i + (step << 1)) : high; //定义二路归并的上界与下界
Rank mid = i + step <= high ? (i + step) : high;
merge(lo, mid, hi);
}
//将i和i+step这两个有序序列进行合并
//序列长度为step
//当i以后的长度小于或者等于step时,退出
step <<= 1;//在按某一步长归并序列之后,步长加倍
}
}
void merge(Rank low, Rank mid, Rank high){
T* A = _elem + low; //合并后的向量A[0, high - low) = _elem[low, high)
int lb = mid - low;
T* B = new T[lb]; //前子向量B[0, lb) = _elem[low, mid)
for (Rank i = 0; i < lb; B[i] = A[i++]); //复制前子向量B
int lc = high - mid;
T* C = _elem + mid; //后子向量C[0, lc) = _elem[mid, high)
//第一种处理方式
for (Rank i = 0, j = 0, k = 0; (j < lb) || (k < lc);) { //B[j]和C[k]中小者转至A的末尾
if (j < lb && k < lc) //如果j和k都没有越界,那么就选择B[j]和C[k]中的较小者放入A[i]
A[i++] = B[j] < C[k] ? B[j++] : C[k++];
if (j < lb && lc <= k) //如果j没有越界而k越界了,那么就将B[j]放入A[i]
A[i++] = B[j++];
if (lb <= j && k < lc) //如果k没有越界而j越界了,那么就将C[k]放入A[i]
A[i++] = C[k++];
}
//第二种处理方式
//for (Rank i = 0, j = 0, k = 0; (j < lb) || (k < lc);) { //B[j]和C[k]中小者转至A的末尾
// if ((j < lb) && (lc <= k || B[j] <= C[k])) //C[k]已无或不小
// A[i++] = B[j++];
// if ((k < lc) && (lb <= j || C[k] < B[j])) //B[j]已无或更大
// A[i++] = C[k++];
//}//该循环实现紧凑,但就效率而言,不如拆分处理
delete[] B; //释放临时空间B
}
find(e, lo, hi)
在区间[lo, hi)内查找目标元素e,返回值是一个秩,如果返回的秩小于 lo,意味着查找失败,否则,返回的秩即为 e 的秩。对于无序向量而言,元素应为可判等的基本类型,或已重载操作符 “==” 或 “!=”;对于有序向量而言,元素应为可比较的基本类型,或已重载操作符 “<” 或 “>” 。
/* 查找操作 */
Rank find(T const & e, Rank lo, Rank hi) const{
//O(hi - lo) = O(n),在命中多个元素时,可返回秩最大者
while((lo < hi--) && e != _elem[hi]); //逆向查找
return hi; //hi < lo意味着失败;否则hi即命中元素的秩
}
search(e, lo, hi)
在区间[lo, hi)内查找目标元素e,返回不大于e且秩最大的元素的秩。这里采用的是二分查找法,适用对象为有序向量,要求向量中的元素是基本类型或已经重载运算符 “<”、“=”。有关二分查找的细节我已经在这篇文章里介绍过了,你真的了解二分查找吗?,感兴趣的朋友可以阅读一下。
可能有的读者不明白「返回不大于e且秩最大的元素的秩」这句话是什么意思,或者说有什么作用。举个例子大家就明白了,假设有这样一个元素类型是整数的有序向量:91,92,93,93,93,97,99,当我查找 93 的时候,返回的最后一个 93 的秩,也就是 4,当我查找 98 的时候,由于向量中没有 98,所以会返回不大于98(也就是小于等于98)且秩最大的元素的秩,也就是 97 的秩—— 5。
这样做的目的是为了方便维护有序向量。由于向量的底层是靠数组来实现的,当我们向有序向量中插入元素时,插入操作会移动大量的数据,这个时候我们会希望尽可能少地移动数据,并且希望插入之后向量依然是有序的。比如,还是以上面那个向量为例,当我们想插入一个 93 时,我们会希望在最后一个 93 之后插入 93,这样移动的数据才最少;当我们想插入一个 98 时,我们会希望在 97 之后插入 98,这样向量才能保证有序。
Rank search(T const & e, Rank lo, Rank hi)
{
while (lo < hi) { //不变性:A[0, lo) <= e < A[hi, n)
Rank mid = (lo + hi) >> 1; //以中点为轴点,经比较后确定深入
(e < _elem[mid]) ? hi = mid : lo = mid + 1; //[lo, mid)或(mid, hi)
}//出口时,A[lo = hi]为大于e的最小元素
return --lo; //即lo-1即不大于e的元素的最大秩
}
deduplicate()
剔除重复元素,返回值是被删除元素的数目。适用对象是所有的向量,且对于无序向量而言,元素应为可判等的基本类型,或已重载操作符 “==” 或 “!=”;对于有序向量而言,元素应为可比较的基本类型,或已重载操作符 “<” 或 “>” 。
//唯一化,删除向量中的重复元素,返回被删除元素数目
int deduplicate()
{
int oldSize = _size; //记录原始规模
Rank i = 1; //从 _elem[i] 开始
while (i < _size) { //自前向后逐一考察各元素 _elem[i]
find(_elem[i], 0, i) < 0 ? //在前缀中寻找雷同者
i++ //若无雷同则继续考察其后继
: remove(i); //否则删除雷同者(至多 1 个?!)
}
return oldSize - _size; //向量规模变化量,即删除元素总数
}
uniquify()
剔除重复元素,返回值是被删除元素的数目。适用对象是有序向量,且要求元素类型为基本类型或已重载运算符 “!=”、“=”。
int uniquify() {
if (disordered())
return -1;
Rank i = 0, j = 0; //各对互异“相邻”元素的秩
while (++j < _size) { //逐一扫描,直至末元素
if (_elem[i] != _elem[j]) { //跳过雷同者,发现不同元素时,向前移至紧邻于前者右侧
_elem[++i] = _elem[j];
}
}
_size = ++i;
return j - i; //向量规模变化量,即被删除元素总数
}
重载 “[]” 运算符
使向量对象可以像数组一样通过间接寻址符 “[]” 来获取元素或操作元素。适用于所有向量。
//重载 “[]” 操作符,返回引用,这样才可以对返回值赋值
int& operator[] (int i) {
return _elem[i];
}
结语
以上就是今天我为大家介绍的向量的全部内容,据我所知,向量是大厂面试时常考的内容哦。看了这篇文章,下次面试官再问你向量就不用怕了!关注微信公众号:AProgrammer,在后台回复「向量」可获得本文完整代码。