软件测试缺陷分析方法简介

ODC分析法

　　ODC（正交缺陷分类）分析方法最早由IBM的waston中心推出，是将一个缺陷在生命周期的各环节的属性组织起来，从单维度、多维度来对缺陷进行分析，从不同角度得到各类缺陷的缺陷密度和缺陷比率，从而积累得到各类缺陷的基线值，用于评估测试活动，指导测试改进和整个研发流程的改进；同时根据各阶段缺陷分布得到缺陷去除过程特征模型，用于对测试活动进行评估和预测。

　　无论测试人员还是开发人员在创建和处理一个缺陷时首先都要添加一些字段内容用于后面的ODC分析。

　　创建缺陷人员需要填写的字段内容主要有：发现缺陷活动、功能模块、结果影响、严重程度和缺陷类型等。处理缺陷人员需要填写的字段内容主要有：开发处理决定、缺陷注入阶段等。（字段可以根据分析需要进行扩充、删减）

　　基于这些字段内容便可以对累计的缺陷数据，根据不同需要单独或两两作出不同维度的数据分析。主要通过数据图表的形式来显示分析结果，常用的图表为饼图（单维度）、直方图（多维度）。通过结果评估测试活动，指导测试改进和研发流程改进。

　　单维度分析主要采用饼图反映所选属性中各类缺陷数量所占比例。如对“功能模块”属性进行单维度分析，目的在于通过各个功能模块的缺陷密度，了解各个功能模块的质量状况。生成的饼图如下：

　　多维度分析采用直方图的方式，结合两个或者多个属性对缺陷进行分析。如使用“功能模块”属性结合“严重程度”属性进行二维度分析。目的在于通过各个模块所产生的缺陷的严重级别了解各个模块的开发质量状况。生成的直方图如下：

　　Gompertz分析法

　　软件测试是为了发现软件产品中存在的缺陷，是软件质量保证的重要阶段。质量、进度和成本是软件项目关注的三大要素，它们互相依赖、互相制约。测试的总目标是充分利用有限的人力、物力，高效率、高质量的完成测试。Gompertz分析方法是在利用已有测试数据的基础上，对测试过程进行定量分析和预测，对软件产品质量进行定量评估，对是否结束测试任务给出判断依据。

我们在日常的软件测试过程中会发现，在测试的初始阶段，测试人员对测试环境不很熟悉，因此日均发现的软件缺陷数比较少，发现软件缺陷数的增长较为缓慢；随着测试人员逐渐进入状态并熟练掌握测试环境后，日均发现软件缺陷数增多，发现软件缺陷数的增长速度迅速加快；但随着测试的进行，软件缺陷的隐藏加深，测试难度加大，需要执行较多的测试用例才能发现一个缺陷，尽管缺陷数还在增加，但增长速度会减缓，同时软件中隐藏的缺陷是有限的，因而限制了发现缺陷数的无限增长。这种发现软件缺陷的变化趋势及增长速度是一种典型的‘S’曲线，满足Gompertz增长模型的应用条件。模型表达式为：

　　Y=a*b^(c^T)

　　其中Y表示随时间T发现的软件缺陷总数，a是当T→∞时的可能发现的软件缺陷总数，即软件中所含的缺陷总数。a*b是当T→0时发现的软件缺陷数，c表示发现缺陷的增长速度。我们需要依据现有测试过程中发现的软件缺陷数量来估算出三个参数a，b，c的值，从而得到拟合曲线函数。

　　对于三个参数a，b，c的估算需要大量复杂的数学计算过程，下面通过一个实例来做简单说明：

　　某测试项目，已经执行测试21周，测试数据如下表所示：

　　通过对以上测试数据进行数学计算并采用“非线性回归最小二乘法”，最终估算出a，b，c三个参数分别为448.685，0.078和0.874。则得到的Gompertz增长模型拟合曲线函数为：

　　Y=a*b^(c^T)=448.685*0.078^(0.874^T)

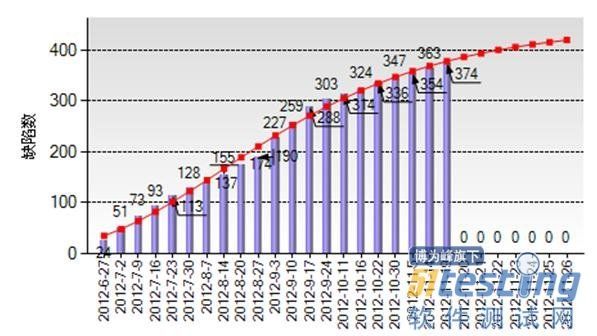
　　生成的曲线图如下：

　　从得到的拟合曲线函数可以看出，该软件产品的总缺陷数估计共有448.685个（极限缺陷数=449）。执行测试21周后，共计发现缺陷数374个，发现缺陷率为83.3%，测试是不充分的。以目前的测试能力来看，若要想将发现缺陷率达到95%，在考虑进一定标准偏差和相关系数前提下，需要发现缺陷数至少达到419.93个。则有：

　　419.93= a*b^(c^T)= 448.685*0.078^(0.874^T)

　　解得T=28，即要测到第28周，还需要再测7周时间可将发现缺陷率提高到95%。之后产品经理就可以根据产品的质量等级、产品成本以及产品进度决定是继续测试还是退出测试。

　　需要说明的是，这个方法使用前提是产品的整个测试活动中测试能力保持相对稳定，同时对测试过程中发现的缺陷只做数量上的处理，不做等级上的划分，这是这个方法的不足之处。

DRE/DRM分析法

　　DRE/DRM分析法是通过已有项目历史数据，得到软件生命周期各阶段缺陷注入和排除的模型，用于设定各阶段质量目标，评估测试活动。

　　缺陷排除效果分析DRE矩阵：

　　DRE主要针对历史数据，矩阵的每一列代表缺陷在何时（什么阶段）引入（产生），每一行代表发现缺陷时开展的工作。矩阵中的数值代表已经发现的缺陷数量。例如：在做代码审查工作时发现1095条缺陷，其中12条是在需求阶段就已经产生，941条是在编码阶段产生。而经过各项测试工作后，发现的缺陷中有1537条是在编码阶段引入。

　　本矩阵的目标是要分别计算出各个阶段的缺陷移除率为后面所用。缺陷移除率的定义为当前阶段工作实际发现的缺陷数量占当前阶段应该发现的缺陷数量的比值。例如：做单元测试时实际发现332条缺陷，在单元测试及之前阶段应该已经发现122+859+939+1537+2=3459条缺陷，而在做单元测试工作之前已经发现730+729+1095=2554条缺陷。就是说单元测试工作本该可以发现到3459-2554=905条缺陷，实际却发现332条缺陷，缺陷移除率为332/905=36.7%。其他阶段的缺陷移除率依此算法都可得到。

　　下面就可以用DRM缺陷排除模型进行项目质量策划。

　　其中“前一阶段泄露的缺陷”等于上一阶段“阶段出口缺陷数”。每个阶段的“注入缺陷”一般来自于历史数据的平均值（经验值）。“缺陷排除有效率”同样来自于对历史数据的计算（前面已经提到）。“排除缺陷数”为我们最终想要的结果，它等于每个阶段还未排除的缺陷数（小计部分）与此阶段的缺陷排除有效率的乘积。从这个结果我们能估算出如果按之前的经验我们在每个阶段应该能发现的缺陷数。如果想降低最终“现场”阶段发现的缺陷，在每个阶段注入缺陷一定的情况下需要提高缺陷排除有效率来达到目的，它的提高意味着每个阶段排除缺陷数量的提高，也是质量目标的提高。