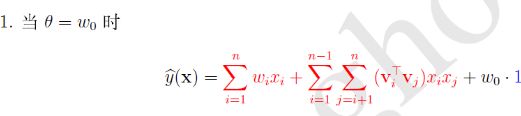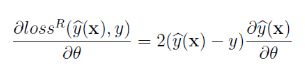个人总结：推荐算法 从MF(LFM) 到 FM FFM Wide&Deep DeepFM

FM

在推荐系统中，经常会碰到电影评分这样高度稀疏的数据，在之前的个人总结：推荐算法篇（附协同过滤等） 综述的基于模型的协同过滤中，提到了FunkSVD(LFM，Latent Factor Model)，通过设置隐含特征，进行矩阵分解，来实现对未知评分的预测。这里FM，和LFM一样，也是隐变量模型。

问题背景

传统逻辑回归认为特征直接是相互独立的，但是很多情况下特征之间的依赖关系不可忽视，因此需进行特征组合，但是大多数业务场景下，类别特征做完onehot后会变得非常稀疏，尤其是特征组合后，特征空间变得很大，而FM就是为了解决特征组合下数据稀疏所带来的问题。

由线性回归说起

一般的线性模型定义如下，很直观可以看出特征均单独出现。

引入二阶多项式，可以引入特征之间的依赖关系

二阶特征的参数共有n(n - 1)/2种，且任意参数间相互独立，并且在进行参数估计时发现，对于这些二次项的参数，都需要大量的非零样本来进行求解，但是很多时候特征空间是相当稀疏的，这种情况下参数的估计值变得相当不准确。

二阶FM原理

FM引入矩阵分解的思路，对交叉项的系数矩阵进行了如下分解：

这个分解的思想是：由于特征之间不是相互独立的，因此可以使用一个隐因子来串联，类似于推荐算法中将一个打分矩阵分解为user矩阵和item矩阵，也就是前面提到的FunkSVD(LFM，Latent Factor Model)，每个user和item都可以用一个隐向量来表示，
FM采用类似思想，将所有二次项系数组成为一个对称矩阵W，W可被分解为V^T*V

V的第j列vj即为第j维特征的隐向量，每一个特征对应一个隐变量，即

特征向量xi和xj的交叉项系数就等于xi对应的隐向量与xj对应的隐向量的内积，即每个参数。

其中为超参数，表示隐向量的长度，因此wij可表示为

两个特征xi和xj的特征组合的权重值，通过特征对应的向量vi和vj的内积表示，这本质上是在对特征进行embedding化表征。

于是模型可以表示为

我们将向量v按行拼成长方阵V

交互矩阵

这里用到了一个结论：当k足够大，对于任意对称正定的实矩阵，均存在实矩阵，使得成立。的对称性可以得到保证，那么如何保证正定性呢？因为我们只关心互异特征之间的相互关系，因此的对角线元素是可以任意取值的，只需将其取的足够大，就可以保证的正定性。

我们希望k取得足够大，但是在高度稀疏的场景下，由于没有足够的样本来估计交互矩阵，因此k通常取得较小。实际上对k（FM的表达能力）的限制，一定程度上可以提高模型的泛化能力。

复杂度分析

直观上看FM的预测复杂度为O(kn^2)，通过化简可以优化至O(kn)

实际应用中，n（特征维数）往往很大，如果是O(kn^2)，就完全没办法被工业界使用了，所以要进行算法复杂度优化。这也是为什么LR（算法复杂度和特征数量n成线性关系）在CTR业界被广泛应用的原因。

在高度稀疏的场景中，特征向量绝大部分分量为0，而关于i的求和只需对非零元素进行，于是复杂度变成了。因此，FM参数训练的复杂度也是O(kn) （一共有n个隐向量，每个隐向量的长度为k，所以参数量是kn，而不是原始的O(n^2)个w，k往往是很小的，远小于n）。

再看看FM的训练复杂度，利用SGD训练模型，模型各个参数的梯度如下：

其中是隐向量的第f个元素，只与f有关，而与i无关，每次迭代过程中，只需计算一次所有f的，就能方便得到所有的梯度。显然计算所有f的的复杂度是O(kn)。已知时，计算每个参数梯度的复杂度是O(1)，得到梯度后，更新每个参数的复杂度是O(1)，模型参数一共有nk+n+1个。因此，FM参数训练的复杂度也是O(kn)。

综上可知，FM可以在线性时间训练和预测，是一种非常高效的模型。

关于隐向量

这里的vi 是xi 特征的低纬稠密表达，实际中隐向量的长度通常远小于特征维度N（一般3、4左右）。在实际的CTR场景中，数据都是很稀疏的category特征，通常表示成离散的one-hot形式，这种编码方式，使得one-hot vector非常长，而且很稀疏，同时特征总量也骤然增加，达到千万级甚至亿级别都是有可能的，而实际上的category特征数目可能只有几百维。FM学到的隐向量可以看做是特征的一种embedding表示，把离散特征转化为Dense Feature，这种Dense Feature还可以后续和DNN来结合，作为DNN的输入，事实上用于DNN的CTR也是这个思路来做的。

多阶FM

可以任意刻画d个特征向量的相互关系

虽然理论上FM可以对高阶特征组合进行建模，但实际上因为计算复杂度的原因一般都只用到了二阶特征组合。

回归与分类

通常优化函数构造为

回归

在回归问题中，一般使用最小平方误差

二分类

1. hinge loss

当y = +1时

当y = -1时

模型训练后用的正负号来预测x的分类。

2. logit loss

在进行二分类时，FM的输出要经过sigmoid变换，这与Logistic回归是一样的。

可见，和越接近，损失越小。

优化方法

目前包括三种

回顾一下模型：

若记模型的参数为

对于任意，存在两个与θ取值无关的函数和。使得成立

具体有

红色部分为，蓝色部分为。

通常计算只用计算，而则利用来计算。

所以关于θ的偏导数为

我们的目标是整体损失函数

于是FM的最优化问题就变为

加入L2正则化，变为

参数集通常较大，如果每个参数都对应一个正则化系数，那么这些正则化系数的确定将会变得很繁琐。因此考虑分组策略，即先对参数进行分组，然后分在同一个组中的参数适用同一个正则化参数，从而减少正则化系数的个数。具体可以：单独一组，按照特征分量的意义可以分成几个组，从而正则化系数集为

表示参数被分到第组。

正则化系数通常通过网格搜索来确定。

使用随机梯度下降训练FM模型，矩阵V的初始化采用符合正态分布的随机初始化。

可见对于一个给定的样本，训练时计算复杂度为。对于一轮迭代计算复杂度就是。

回归时使用均方误差

在分类时使用logit loss

FM与SVM的比较

我们都知道SVM的决策函数为

其中n为样本数量，K为核函数。前面的yi αi以及xi合在一起就是wi。于是线性的SVM决策函数可以写为

如果使用多项式核

当d=2时，模型函数可以表示为

这里就出现了二次项，可以看做是特征组合，和FM的二次项十分相似。但是区别在于，SVM的二元特征交叉参数是独立的，而FM的二元特征参数是由两个向量相乘，由于其他参数也可能用到这两个向量中的某一个，于是该参数就与其他参数相互影响，并非独立，比如和不是相互独立的。

而多项式SVM在稀疏条件下并没有很好的表现，这是因为它需要在训练集上共现才能被学习，而稀疏条件下无法达到这种条件，因此表现不如人意，而FM可以提取更深层次的抽象意义，表现更加良好。同时，FM的训练和预测复杂度是线性的，而二阶多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。

 

从FM到FFM

举个例子，假设有三个字段分别可以代表媒体，广告主和具体商品，性别。其中媒体有5种数据，广告主有10种数据，性别有男女2种，经过onehot后，每个样本有17个特征，其中只有3个特征非空。

如果使用FM，则17个特征，每个特征对应1个隐变量，一共有17个隐变量。我们的W矩阵最后就是这17个隐变量两两相乘而得到。

如果使用FFM，则17个特征，每个特征对应3个隐变量，即每个特征对应每一个类型（field）有一个隐变量，具体来说就是每个特征对应媒体，广告主，性别三个field各有一个隐变量。一共有17x3个隐变量，参数扩大了3倍。

类似FM，可以得出FFM模型

表示特征i与特征j互作用时对应的向量，f_j代表j对应的field。

举个例子：

上图的红色数字对应的field，蓝色对应的是特征，绿色对应的是值（1是因为离散特征被onehot了，连续特征未进行处理，也可以离散化处理）。

损失函数与优化

与FM类似，FFM也可以用于回归和分类问题，当面对回归问题时使用MSE，面对分类问题时使用logistic loss

这里假设是分类问题，于是损失函数可以定义为

同理我们可以采用随机梯度下降来进行优化。

国立台湾大学在Criteo比赛中提出了FFM，并对其进行了C++实现：github。该版本省略了常数和一次项，模型方程如下：

且在该版本中采用Logistic loss以及L2惩罚项作为损失函数，因此该版本只能用于二元分类问题

FFM数据预处理

样本归一化

需对样本进行归一化，防止数据溢出，造成梯度计算失败。即在该版本中设置pa.norm为真。

特征归一化

由于数值特征和类别特征本身处于不同量纲，因此在样本归一化后，容易产生诡异的样本值，如销量5000和性别男性（1），归一化后使得性别的值略小于0.0002，而销量近似1，这使得性别在最后的模型方程中产生很小的作用。因此需要对每个特征再次单独进行归一化。

零值特征

零值特征在模型方程中无法体现作用，因此被省略。这会为稀疏样本的运行提升速度。

 

Wide&Deep

wide&deep主要分为两部分，wide部分就是传统的LR模型，deep部分就是DNN，整个模型结构如下

wide部分是一个LR模型，而Deep部分就是DNN。Wide&Deep将两者的优点结合到一起。

Wide部分

wide输入的特征部分包括基础特征和交叉特征，这里的交叉特征是人工构建的，通过对数据的了解，构建这种特征可以捕捉两个特征间的交互，起到添加非线性的作用。交叉特征可表示为

是布偶变量，两项特征交叉，于是只有该两项特征对应的为1，其余为0，于是只与对应的两项特征的值有关，只有特征值均为1时，才为1。比如性别和语言的交叉特征，我们认定性别为男，语言为中文时，该交叉特征为1，除此之外其他条件均为0。

最后的wide部分的输出为

Deep部分

deep部分先将稀疏高维的类别特征转化为低维的稠密向量，通常也是使用embedding的方式，嵌入向量的维度数量级通常在O(10)到O(100)，然后将得到的嵌入向量输入隐层，进行前向传播，这里用的激活函数一般是ReLU。

l代表层数，f是激活函数。W、a、b分别代表权重，输入以及偏置。最终通过反向传播更新嵌入向量。

Joint of Wide&Deep

从模型的图中，可以很清晰地看出是将Wide与Deep模型进行了融合，其模型为

也就是将两部分的值简单相加，再加入偏置后输入激活函数，就得到了最后的估计值。

联合训练

Wide&Deep使用的是联合训练，而GBDT+LR采用的是集成训练。集成训练是独立训练，也就是说先训练GBDT，再训练LR。而联合训练是同时训练两部分同时产出，然后使用反向传播进行优化。

在训练时，Wide部分主要是为了弥补Deep部分的缺陷，所以主要采用了小规模的交叉特征实现，使用Follow-the-regularized-leader（FTRL）算法以及L1正则化算子。Deep部分使用AdaGrad算法进行优化。

 

从FM和Wide&Deep到DeepFM

由于在Wide&Deep中wide部分需要人工构建交叉特征，而FM的优势就在于能够自动构建交叉特征，所以wide部分直接使用FM，就能省去构建人工特征的部分。

在输入上，FM和DNN共享原始特征，保证模型特征的准确与一致性。下面是DeepFM的基本结构

虽然这里提到了Field，但是纵观论文通篇没有提到FFM，所以这里生成embedding还是使用的FM。这里Field内部的特征为特征进行onehot编码后的表示。

最后输出表示为

FM部分

结合公式来看

Inner Product部分就体现了二阶交叉特征，而Addition部分体现的是一阶特征。

Deep部分

首先看一下子网络细节

每个field在进行onehot后输入网络，由于field特征长度不同，但是子网络输出的向量需具有相同维度，论文中设置的embedding size为5。当输入一个样本时，对于每一个field，我们可以看到，只有在为1的那个特征，会将该特征对应的所有权重（这里是5个）映射为embedding向量，也就是说，训练第一层的权重就是在训练embedding，embedding就隐藏在权重中。

这里需要提醒的是，FM训练的隐向量数量是和onehot后对应的特征数量相同的，所以这里其实就通过每次输入不同的样本，可以训练到不同的隐变量（embedding vector）。

关于初始化，文中没有使用FM预训练embedding的方法，取而代之的是，将FM和DNN整合到一起来对embedding进行训练，它们共享第一层的权重。

将embedding的输出表示为

ei是第i个field的embedding，其中m是fields的数量。将这一层的输出继续输出到深度神经网络中，前向传播的过程为

l代表层的深度。a、W、b分别代表输出，权重和偏置。

效果

在多个数据集对比多个算法，显示出了DeepFM的优越性。

调参

使用不同激活函数的效果

Dropout:神经元被保留在网络中的概率

每层神经元的数量

隐层的数量

网络形状