如何直观的理解傅里叶变换?
文章目录
- 1. 直观解释
- 2. 时域:旋转与傅立叶级数
- 2.1 欧拉公式
- 2.2 火星的轨迹曲线
- 2.3 旋转的傅立叶
- 3. 频域:线性代数与傅立叶级数
- 3.1 线性代数
- 3.2 傅立叶级数的基
- 3.3 傅立叶级数向量
- 3.4 频谱图
- 3.5 应用
- 3.5.1 图像压缩
- 3.5.2 模式识别
- 4 傅立叶级数和傅立叶变换
彩虹,大概是我们在自然界中最容易观察到的傅立叶级数。
1. 直观解释
1666年牛顿发现太阳光经三棱镜的折射后可呈现彩色光,称为光的色散现象:
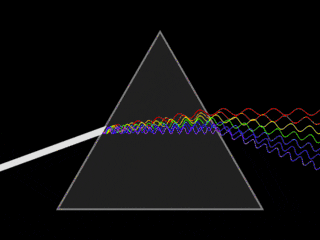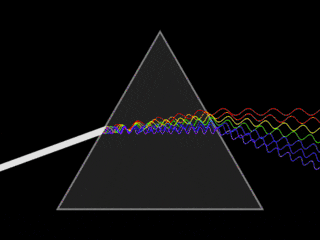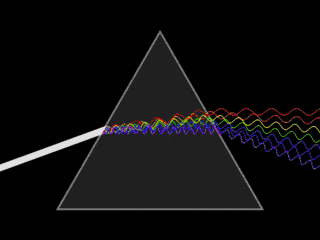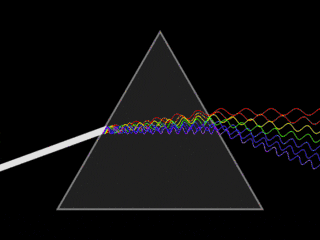
先说一个物理常识,光是一种波,而光的颜色由振幅和频率所决定。
所以色散实际上是,白色的光波被分解为七色光波(实际应该是无数种颜色的光波):

七色光波可以用正弦波 a n s i n ( n x ) a_nsin(nx) ansin(nx)(其中 a n a_n an是振幅, n x n_x nx可以表示频率)来近似。因此上面实际就是傅立叶级数(下面只是傅立叶级数的非常不准确的近似,为了帮助理解简化成了这样子,后面会给出严格定义):
白 色 = ∑ a n s i n ( n x ) 白色=\sum a_n sin(nx) 白色=∑ansin(nx)
雨过天晴,有时就会看见彩虹:

雨后空气中的水分就好像无数的三菱镜,把太阳光拆成了彩色。正是大自然中的色散现象。
这大概是我们在自然界中最容易观察到的傅立叶级数。
2. 时域:旋转与傅立叶级数
更细致的推导,可参考此文:如何理解傅立叶级数公式?。
现在给出傅立叶级数的严格形式,以弥补之前的近似。
假设,f(x)为周期为T的函数,并且满足傅立叶级数的收敛条件,那么可以写作傅立叶级数:
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos ( 2 π n x T ) + b n sin ( 2 π n x T ) ) f(x)={\frac{a_{0}}{2}}+\sum _{{n=1}}^{\infty}\left(a_{n}\cos({\tfrac {2\pi nx}{T}})+b_{n}\sin({\tfrac {2\pi nx}{T}})\right) f(x)=2a0+n=1∑∞(ancos(T2πnx)+bnsin(T2πnx))
其中:
a n = 2 T ∫ x 0 x 0 + T f ( x ) ⋅ cos ( 2 π n x T ) d x b n = 2 T ∫ x 0 x 0 + T f ( x ) ⋅ sin ( 2 π n x T ) d x a_{n}={\frac {2}{T}}\int _{{x_{0}}}^{{x_{0}+T}}f(x)\cdot \cos({\tfrac {2\pi nx}{T}})\ dx\\ b_{n}={\frac {2}{T}}\int _{{x_{0}}}^{{x_{0}+T}}f(x)\cdot \sin({\tfrac {2\pi nx}{T}})\ dx an=T2∫x0x0+Tf(x)⋅cos(T2πnx) dxbn=T2∫x0x0+Tf(x)⋅sin(T2πnx) dx
2.1 欧拉公式
根据欧拉公式:
e i θ = cos θ + i sin θ e^{i\theta } = \cos \theta +i\sin \theta eiθ=cosθ+isinθ
我们可以推出:
sin θ = e i θ − e − i θ 2 i cos θ = e i θ + e − i θ 2 \sin \theta ={\frac{e^{{i\theta }}-e^{{-i\theta }}}{2i}} \\ \cos \theta ={\frac{e^{{i\theta }}+e^{{-i\theta }}}{2}} sinθ=2ieiθ−e−iθcosθ=2eiθ+e−iθ
根据上式,我们可以写出傅立叶级数的另外一种形式:
f ( x ) = ∑ n = − ∞ ∞ c n ⋅ e i 2 π n x T f(x)=\sum _{{n=-\infty}}^{\infty}c_{n}\cdot e^{{i{\tfrac {2\pi nx}{T}}}} f(x)=n=−∞∑∞cn⋅eiT2πnx
其中:
c n = 1 T ∫ x 0 x 0 + T f ( x ) ⋅ e − i 2 π n x T d x c_{n}={\frac{1}{T}}\int _{{x_{0}}}^{{x_{0}+T}}f(x)\cdot e^{{-i{\tfrac {2\pi nx}{T}}}}\ dx cn=T1∫x0x0+Tf(x)⋅e−iT2πnx dx
看到复数也不要怕,根据之前的文章“如何通俗易懂地解释欧拉公式?”,看到类似于 e i θ e^{i\theta} eiθ这种就应该想到旋转:

从这角度来看,傅立叶级数:
f ( x ) = ∑ n = − N N c n ⋅ e i 2 π n x T \displaystyle f(x)=\sum _{{n=-N}}^{N}c_{n}\cdot e^{{i{\tfrac {2\pi nx}{T}}}} f(x)=n=−N∑Ncn⋅eiT2πnx
实际上就是说,曲线可以理解为无数旋转的叠加,这怎么理解呢?看下面的例子。
2.2 火星的轨迹曲线
比如这是地球上观察到的火星运行的轨迹:

可以通过两个圆周运动的叠加来模拟出这个曲线:

其实这就是地心说,感兴趣可以看下“爱因斯坦和牛顿是否被严重高估了?”。
通过这种圆环套圆环的做法,可以模拟各种复杂的图形,比如可以画出辛普森。
注(多圆环嵌套画出辛普森):
YouTube地址:
https://www.youtube.com/watch?v=QVuU2YCwHjw;
腾讯视频地址:
https://v.qq.com/x/page/t0567u5oy2g.html
2.3 旋转的傅立叶
所以,傅立叶级数实际上就是把f(x)看作是圆周运动的组合。
只是x是不断变大的,而不是绕着圆变换的,所以就画出了函数曲线:
不断增大的x就好像是时间流逝,永不回头,所以也称为“时域”。
3. 频域:线性代数与傅立叶级数
时域是现实存在的,频域却是生造的了,理解起来更加抽象。
但,频域是傅立叶级数(变换)更本质的内容。
把傅立叶级数(变换)视作圆周运动的组合,是比较粗浅的看法,是买椟还珠的作法。
而把傅立叶级数(变换)看作频域,等于直接把它绑上了线性代数的战车,把它从固定在发射井中的常规核武器变成了游走不定更具威力的核潜艇、核卫星。
3.1 线性代数
线代的最基本的研究对象就是向量,带箭头的一根直线:

线代的基本操作就是把向量分解为基的合成:

即:
u ⃗ = a i ⃗ + b j ⃗ \vec{u_{}}=a\vec{i_{}}+b\vec{j_{}} u=ai+bj
这么做的好处很多,比如物理中,分析各个方向上的受力,然后进行合成:

比如,如果a >> b,我们就可以知道, i ⃗ \vec{i_{}} i上的分量更重要, j ⃗ \vec{j_{}} j方向上的分量可以丢掉。(关于这个内容可以参看“如何通俗地理解奇异值?”)。
线性代数还有很多好处,在使用傅立叶级数的时候就会感受到。
3.2 傅立叶级数的基
傅立叶级数(变换)本身是线性的(这个就是比较抽象的线性了),因此可以把线性代数在傅立叶级数上进行推广。
让我们先找到傅立叶级数的基是什么。
为了说明方便,假设f(x)的周期 T = 2 π T=2\pi T=2π,那么有:
f ( x ) = ∑ n = − ∞ ∞ c n ⋅ e i n x f(x)=\sum _{n=-\infty}^{\infty}c_{n}\cdot e^{inx} f(x)=n=−∞∑∞cn⋅einx
其中,以下无穷集合:
{ e i n x } , n ∈ N \{e^{inx}\},n\in\mathbb{N} {einx},n∈N
是无限维向量空间中的一组基,而且还是正交单位基。
可是,函数为什么可以做基啊?怎么有无限个基啊?无限维向量空间又是什么啊?这个可以看另一篇文章的具体推导。
3.3 傅立叶级数向量
f(x)可以写作:
f ( x ) = ⋯ + c − 1 e ( − 1 ) ⋅ i x + c 0 e ( 0 ) ⋅ i x + c 1 e ( 1 ) ⋅ i x + c 2 e ( 2 ) ⋅ i x + ⋯ f(x)=\cdots+c_{-1}e^{(-1)\cdot ix}+c_{0}e^{(0)\cdot ix}+c_{1}e^{(1)\cdot ix}+c_{2}e^{(2)\cdot ix}+\cdots f(x)=⋯+c−1e(−1)⋅ix+c0e(0)⋅ix+c1e(1)⋅ix+c2e(2)⋅ix+⋯
因为 { e i n x } , n ∈ N \{e^{inx}\},n\in\mathbb{N} {einx},n∈N是基,所以可把f(x)表示为一个向量:
f ( x ) = ( ⋯ , c − 1 , c 0 , c 1 , c 2 , ⋯ ) f(x)=(\cdots, c_{-1}, c_0, c_1, c_2, \cdots) f(x)=(⋯,c−1,c0,c1,c2,⋯)
这个向量其实就是傅立叶级数的向量。
因为基 { e i n x } , n ∈ N \{e^{inx}\},n\in\mathbb{N} {einx},n∈N实际上反映了周期运动的频率,我们以频率为基,所以这样看待傅立叶级数的方式就是“频域”。
3.4 频谱图
对于:
f ( x ) = ∑ n = − ∞ ∞ c n ⋅ e i n x f(x)=\sum _{n=-\infty}^{\infty}c_{n}\cdot e^{inx} f(x)=n=−∞∑∞cn⋅einx
我们用 ( n , c n ) (n,c_n) (n,cn)来描点作图,就得到频谱图。
下面是一个周期矩形波的频谱图:

3.5 应用
3.5.1 图像压缩
在“如何通俗地理解奇异值?”一节,里面就说过图像压缩的问题。
傅立叶级数通过同样的原理也可以做图像压缩,比如JPG就是用傅立叶进行图片压缩的。
原理可以大概这么理解,哪些基上的坐标值特别小,就可以丢掉,这样就可以压缩图像。
这就是把函数分解到正交基上的好处,我们可以用线性代数中的知识直接去处理。
信号处理中还有不少类似的分解,比如小波变换。所以掌握数学思想尤为重要。
3.5.2 模式识别
类似的图像,通过傅立叶变换,转换到频域之后看起来确实比较类似,比如下面这幅图,A的频域看起来就挺像,而A、B、C、D之间看起来就不太一样:
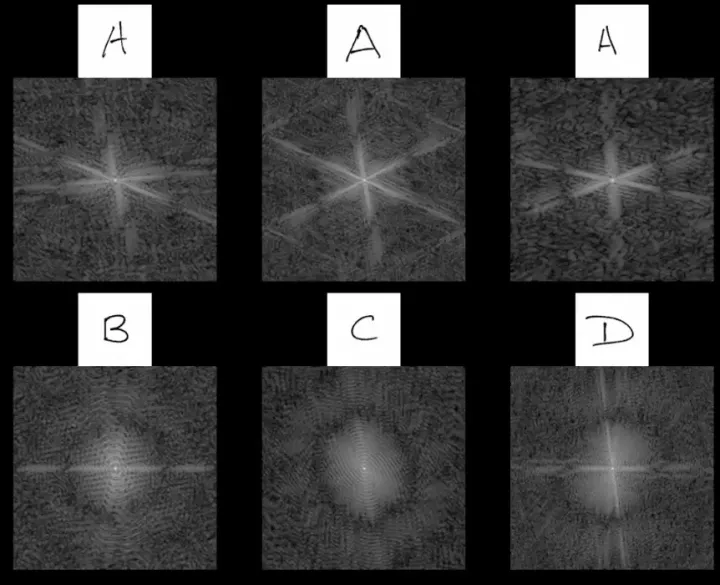
我们人眼观察图片的方法对计算机并不适用,似乎对于计算机而言,频域更能揭示“特征”。
4 傅立叶级数和傅立叶变换
傅立叶级数是基于周期函数的,如果把周期推广到 ,那么也就变为了非周期函数,这就是傅立叶变换。
两者的频谱图对比,可以看到傅立叶变换的频谱图是连续的(上面是周期函数的傅立叶级数分解,下面是非周期函数的傅立叶变换):

最后,介绍一个可以完成傅立叶级数的机械装置,非常好玩:
视频地址:https://v.qq.com/x/page/v05675wtvhj.html
来源:马同学高等数学
https://www.matongxue.com/