数据结构之Java实现底层BinarySearchTree

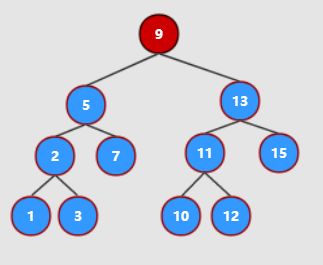
数组、栈、队列和链表都是一种线性数据结构，树形数据结构是一类重要的非线性数据结构。树形数据结构可以表示数据表素之间一对多的关系。其中以树与二叉树最为常用，树是以分支关系定义的层次结构。树只有一个根结点，对于二叉树父结点至多有两个子结点，每个子结点只有父结点，结点的无子结点，表明此结点是叶子结点，对于二叉树每一个结点都有左右子结点称为满二叉树。二分搜索树是二叉树的一种，其要求左子树比根结点的值都要小，左子树比父结点值都要小，而对于右子树都要比根结点都要大，右子树比父结点都要大，结构如下图

对于二分搜索树的数据结构的实现采用了递归思想，对于每一个结点来说都是一棵子树，下面是主要实现代码

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

//二分搜索树是有一定顺序存储数据(有明确的比较规则)，所以数据类型必须实现Comparable接口
public class BST> { 
 private class Node {  //定义了一个私有的结点内部类
  public E e;    //声明存储数据
  public Node left, right;//声明左右结点

  public Node(E e) {  //有参构造函数，根据传入数据生成结点
   this.e = e;
   left = null;
   right = null;
  }
 }

 private Node root;   //声明根结点
 private int size;   //声明树大小

 public BST() {    //无参构造函数，根节点为空，大小为0
  root = null;
  size = 0;
 }

 public int size() {   //返回树大小
  return size;
 }

 public boolean isEmpty() { //判断树是否为空
  return size == 0;
 }

 public void add(E e) {      //向树中添加一个元素，内部是调用一个私有重载函数
  root = add(root, e);
 }
 
 //添加元素时真正调用的函数，无需对用户开放，采用递归的思想
 private Node add(Node node, E e) {
  //递归终止条件，当节点为空时，将待插入元素形成一个新节点返回
  if (node == null) {
   size++;
   return new Node(e);
  }
  //如果插入元素比该结点值小，向左子树搜索
  if (e.compareTo(node.e) < 0) {
   node.left = add(node.left, e);
  }
  //如果插入元素比该结点值大，向右子树搜索
  else if (e.compareTo(node.e) > 0) {
   node.right = add(node.right, e);
  }
  return node; 
 }

 public boolean contain(E e) {  //查看树中是否包含输入元素，内部是调用一个私有重载函数
  return contain(root, e);
 }
 
 //判断是否包含元素时真正调用的函数，无需对用户开放，采用递归的思想
 private boolean contain(Node node, E e) {
  //当搜索到结点为空时，递归终止，返回false
  if (node == null) {
   return false;
  }
  //当输入元素与结点值相等，则返回true
  if (e.compareTo(node.e) == 0)
   return true;
  //输入元素比结点值要小，向左子树递归搜索
  else if (e.compareTo(node.e) < 0) {
   return contain(node.left, e);
  }
  //否则，向右子树递归搜索
  else {
   return contain(node.right, e);
  }
 }
 
 public void preOrder() {  //前序遍历二分搜索树
  preOrder(root);
 }
 
 //私有化该前序遍历函数，采用递归思想
 private void preOrder(Node node) {
  //递归终止条件
  if (node == null)
   return;
  //首先使用当前结点元素，再遍历左子树，右子树
  System.out.println(node.e);
  preOrder(node.left);
  preOrder(node.right);
 }

 public void preOrderNR() {  //采用非递归方式前序遍历
  //定义一个栈，将根结点压入栈中
  Stack stack = new Stack<>();
  stack.push(root);
  //遍历整个栈
  while (!stack.isEmpty()) {
   //弹栈赋给当前结点
   Node cur = stack.pop();
   System.out.println(cur.e);
   //由于栈是先进后出，先要入栈的是右结点，后面是右结点，在出栈时是左结点先出
   if (cur.right != null)
    stack.push(cur.right);
   if (cur.left != null)
    stack.push(cur.left);
  }
 }

 public void inOrder() {  //中序遍历，可以对树排序输出
  inOrder(root);
 }

 //私有化该中序遍历函数，采用递归思想
 private void inOrder(Node node) {
  //递归终止条件
  if (node == null)
   return;
  //递归遍历左子树，再使用当前元素，最后遍历右子树
  inOrder(node.left);
  System.out.println(node.e);
  inOrder(node.right);
 }

 public void inOrderNR() { // 采用非递归方式中序遍历
  //创建一个栈
  Stack stack = new Stack<>();
  //生成一个结点指向根结点
  Node cur = root;
  //开始遍历整个树
  while (cur != null || !stack.empty()) {

   //将树最左边元素依次压入栈中
   while (cur != null) {
    stack.push(cur);
    cur = cur.left;
   }
   //弹栈赋给当前结点
   cur = stack.pop();
   //使用当前结点
   System.out.print(cur.e + " ");
   //将当前结点指向当前结点的右结点
   cur = cur.right;
  }
 }

 public void postOrder() {  //后序遍历
  postOrder(root);
 }

 //私有化该后序遍历函数，采用递归思想
 private void postOrder(Node node) {
  //递归终止条件
  if (node == null)
   return;
  //遍历左子树，然后遍历右子树，最后使用当前元素
  postOrder(node.left);
  postOrder(node.right);
  System.out.println(node.e);
 }

 public void postOrderNR() { // 采用非递归方式后序遍历
  Stack stack = new Stack<>(); //创建一个栈
  Node pre = null; //创建一个前驱结点
  Node cur = root; //创建当前结点指向根结点
  //循环遍历整棵树
  while (cur != null || !stack.empty()) {
   //将最左边元素依次压入栈中
   if (cur != null) {
    stack.push(cur);
    cur = cur.left;
   }
   else
   { //弹栈赋给当前结点
    cur = stack.pop();
    //如果当前结点右结点为空或者前驱结点为右节点，那么就使用当前结点，前驱结点赋给当前结点
    if (cur.right == null || pre == cur.right) {
     System.out.printf(cur.e + " ");
     pre = cur;
     cur = null;
    }
    //否则将当前结点压入栈中，指向当前结点的右节点
    else {
     stack.push(cur);
     cur = cur.right;
    }
   }
  }
 }

 //层序遍历，广度优先准则，使用队列完成层序遍历
 public void levelOrder() {
  //生成一个队列
  Queue q = new LinkedList<>();
  q.add(root);  //根结点入队
  //循环遍历整个队列
  while (!q.isEmpty()) {
   //出队赋给当前结点，并使用
   Node cur = q.remove();
   System.out.println(cur.e);
   //左结点非空则入队，右结点非空则入队
   if (cur.left != null)
    q.add(cur.left);
   if (cur.right != null)
    q.add(cur.right);
  }
 }

 //采用两个函数实现获取树中最小元素，从根结点一直往左延伸，直到某个结点左结点为空
 public E minimum() {
  return minimum(root).e;
 }

 private Node minimum(Node node) {
  if (size == 0)
   throw new IllegalArgumentException("BST is empty!");
  if (node.left == null)
   return node;

  return minimum(node.left);
 }

 //采用两个函数实现获取树中最大元素，从根结点一直往右延伸，直到某个结点右结点为空
 public E maximum() {
  return maximum(root).e;
 }

 private Node maximum(Node node) {
  if (size == 0)
   throw new IllegalArgumentException("BST is empty!");
  if (node.right == null)
   return node;

  return maximum(node.right);
 }

 //删除最小值函数
 public E removeMin() {
  E ret = minimum();
  root = removeMin(root);
  return ret;
 }

 private Node removeMin(Node node) {
  if (node.left == null) {
   Node rightNode = node.right;
   node.right = null;
   size--;
   return rightNode;
  }
  node.left = removeMin(node.left);
  return node;
 }

 //删除最小值函数
 public E removeMax() {
  E ret = maximum();
  root = removeMax(root);
  return ret;
 }

 private Node removeMax(Node node) {
  if (node.right == null) {
   Node leftNode = node.left;
   node.left = null;
   size--;
   return leftNode;
  }
  node.right = removeMin(node.right);
  return node;
 }

    public void remove(E e){ //实现任意元素删除
        root = remove(root, e);
    }
 
    //删除元素真正调用函数
 private Node remove(Node node, E e) {
  //递归终止条件
  if (node == null)
   return null;
  //输入元素比该结点元素值小，向左子树递归
  if (e.compareTo(node.e) < 0) {
   node.left = remove(node.left, e);
   return node;
  }
  //输入元素比该结点元素值大，向右子树递归
  else if (e.compareTo(node.e) > 0) {
   node.right = remove(node.right, e);
   return node;
  }
  //输入元素与该节点元素相等
  else {
   // 待删除节点左子树为空的情况
   if (node.left == null) {
    Node rightNode = node.right;
    node.right = null;
    size--;
    return rightNode;
   }

   // 待删除节点右子树为空的情况
   if (node.right == null) {
    Node leftNode = node.left;
    node.left = null;
    size--;
    return leftNode;
   }
   //左右子树都非空
   Node successor = new Node(minimum(node.right).e);
   size++;

   successor.right = removeMin(node.right);
   successor.left = node.left;

   node.left = node.right = null;
   size--;

   return successor;
  }
 }

 @Override
 public String toString() {
  StringBuilder res = new StringBuilder();
  generateBSTString(root, 0, res);
  return res.toString();
 }

 private void generateBSTString(Node node, int depth, StringBuilder res) {
  if (node == null) {
   res.append(generateDepthString(depth) + "null\n");
   return;
  }
  res.append(generateDepthString(depth) + node.e + "\n");
  generateBSTString(node.left, depth + 1, res);
  generateBSTString(node.right, depth + 1, res);
 }

 private String generateDepthString(int depth) {
  StringBuilder res = new StringBuilder();
  for (int i = 0; i < depth; i++) {
   res.append("--");
  }
  return res.toString();
 }
}

以上就是二分搜索树整个实现过程。