一、感知机
感知机(perceptron)由美国学者Frank Rosenblatt在1957年提出的。
1、感知机的定义
接收多个输入信号,输出一个信号。
感知机与神经元(节点)的区别:
感知机由神经元构成。
感知机的多个输入信号都有各自的权重,权重发挥控制各个信号的重要性的作用。
2、简单逻辑电路
与门:两个输入均为1时输出1,其他输出0
与非门:两个输入均为1时输出0,其他输出1
异或门:两个输入信号不相同时,输出1,其他输出0
权重w1,w2是控制输入信号的重要性的参数
偏置是调整整个神经元被激活的容易程度的参数。如b=-20.0,则输入信号的加权总和必须超过20.0,神经元才会被激活。
import numpy as np
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))
用单层感知机无法实现异或门。
使用与门、与非门、或门实现异或门。与门、或门是单层感知机,异或门是2层感知机。
import numpy as np
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def XOR(x1,x2):
s1 = NAND(x1,x2)
s2 = OR(x1,x2)
y = AND(s1,s2)
return y
print(XOR(0,0))
print(XOR(1,0))
print(XOR(0,1))
print(XOR(1,1))
二、神经网络
神经网络由输入层、输出层、中间层(隐藏层)组成。有2层包含权重的,称为2层网络。
激活函数:将输入信号的总和转换为输出信号。感知机和神经网络的主要区别就在激活函数上。
1、阶跃函数
def step_function(x):
if x > 0:
return 1
else:
return 0
用numpy实现阶跃函数
x = np.array([-1.0,1.0,2.0])
y = x > 0
y = y.astype(np.int)
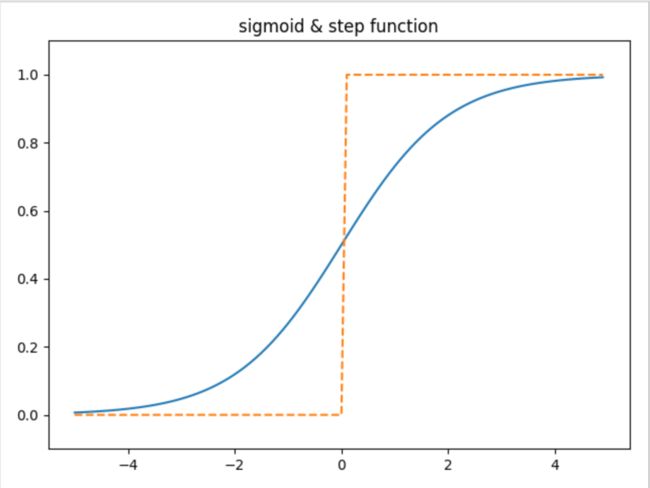
2、sigmoid函数实现
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
def step_function(x):
return np.array(x>0,dtype=np.int)
x = np.arange(-5.0,5.0,0.1)
y1 = sigmoid(x)
y2 = step_function(x)
plt.plot(x,y1,label="sigmoid")
plt.plot(x,y2,linestyle="--",label="阶跃函数")
plt.ylim(-0.1,1.1)
plt.show()
神经网络的激活函数必须使用非线性函数。原因1:线性函数使加深网络层数无意义,多层神经网络,总能找到与之等效的无隐藏层神经网络。
3、ReLU函数
def relu(x):
return np.maximum(0,x)
4、内积
import numpy as np
X = np.array([1,2])
W = np.array([[1,3,5],[2,4,6]])
Y = np.dot(X,W)
print(Y)
5、符号定义
(1)代表第1层权重,2代表前一层的第2个神经元,1代表后1层的第1个神经元。
用公式表示神经网络
第一层使用矩阵乘法的加权和表示:
两层神经网络的代码实现
import numpy as np
from deeplearning.sigmoid import *
def init_network():
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def identity_function(x):
return x
def forward(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1)+b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)
机器学习的问题大致分为两类:分类、回归。分类使用softmax函数,回归用恒等函数。为什么分类问题会用softmax,因为softmax函数的特征,就是输出的总和为1,选中其中概率最高的作为分类结果。
实现softmax函数
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
将数据限定到某个范围内的处理,称作正规化。
三、神经网络的学习
神经网络的特征就是可以从数据中学习。数据是机器学习的核心。
实际的神经网络中国,参数的数量成千上万。
如何识别手写5的数字?从图像中提取特征量,学习特征量的模式,特征量指可以从输入数据中准确提取本质数据的转换器。
机器学习,特征量由人工设计。
神经网络,重要的特征量都是由机器学习的。
泛化能力,处理未被观察过的数据的能力。获得泛化能力是机器学习的终极目标。避免过拟合是机器学习的一个重要课题。
神经网络中用于表示学习拟合程度指标是,损失函数。
损失函数:均方误差
表示神经网络的输出,表示进度数据
均方误差实现
def mean_squared_error(y,t):
return 0.5 * np.sum((y-t)**2)
交叉熵误差
神经网络学习中,不能用识别精度作为指标的原因是,参数的导数在绝大多数地方会变为0。调整参数,变化是不连续的、离散的值。
为什么不能用阶跃函数作为激活函数,原因就是阶跃函数不平滑,不能做到连续的微调。sigmoid的导数则是连续变化的。
导数实现
def function_1(x):
return 0.01*x**2 + 0.1*x
y = numerical_diff(function_1,5)
print(y)
机器学习的主要任务是在学习时,寻找最优参数。
梯度下降实现
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
超参数:学习率等参数,由人工设定。
极小值,是某个范围内的最小值。
鞍点:某个方向看是最小值,从另一个方向看是最大值的点。