算法入门---java语言实现的二分搜索树小结
图片均来自慕课网,仅仅为了学习记录。
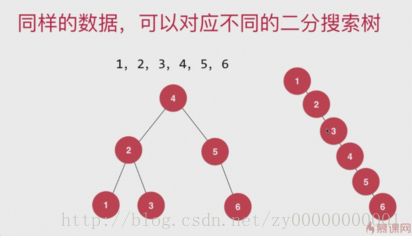
1、二叉查找树(Binary Search Tree)
也可叫做二分查找树。它不仅可以查找数据,还可以高效地插入、删除数据。
特点:
每个节点的key值大于左子节点,小于右子节点。注意它不一定是完全的二叉树。
所以节点的key是唯一的,我们就是通过它来索引key对应的value,注意图中标注的都是key哦。

所以二叉搜索树也不适合用数组来表示,一般都是用node节点来表示。
相比数组的数据结构的优势:

2、实现。
先实现每一个节点:
节点的要素有key、value、左子节点、右子节点。
public class Node { //Node的key private int mKey; //Node对应的value值 private int mValue; //左子节点和右子节点,初始状态的时候都为null. private Node mLeftChild; private Node mRightChild; public Node(int key,int value){ mKey = key; mValue = value; mLeftChild = null; mRightChild = null; } public int getValue(){ return mValue; } public Node getLeftChild(){ return mLeftChild; } public Node getRightChild(){ return mRightChild; } public void setValue(int newValue) { mValue = newValue; } public void setLeftChild(Node left) { mLeftChild = left; } public void setRightChild(Node right) { mRightChild = right; } public int getKey(){ return mKey; }}
二叉查找树的基本实现
package com.zy.serch;/** * 二分查找树 * @author Administrator * */public class BinarySearchTree { //根节点. private Node mRoot; //还应该有个来记录数量的值,每插入一个就应该数据加1. private int mCount; public int getSize(){ return mCount; } //判空 public boolean isEmpty(){ return mCount == 0; } }
插入数据的实现
/** * 供用外部调用的 * @param key 外部要存储的数据的key * @param value 外部要存储的数据的值 */ public void insert(int key,int value){ //进一步调用内部的insert,把当前的key和value放入到以mRoot为根节点的树当中。 mRoot = insert(mRoot, key, value); } /** * 插入一个节点. * 核心思想:从根节点开始找插入的位置,满足二叉搜索树的特性,比左子节点大,比右子节点小. * 步骤: * 1、从根节点开始,先比较当前节点,如果当前节点为null那么很明显就应该插入到这个节点。 * 2、如果上面的节点不是null,那么和当前节点比较,如果小于节点就往左子树放,如果大于节点就往右子树放。 * 3、然后分别对左子树或者右子树递归的递归进行如上1、2步骤的操作 * * 此时就用到了递归,那么递归是对某一个问题,它的子问题需要是同样的模型。 * 此处的一个小的问题就是:对某个node,然后进行操作,所以参数应该有个node才能实现循环起来。 * 此处向以node为根的二叉搜索树中,插入节点(key, value).此处就都用int类型了,外部的用户是 * 不需要了解node的概念.它们只需要知道传入的的key和value就行。 * 暂时的设计便于理解传入用户自己的key和value,到时候也方便用于自己根据key进行所以. * * @param node 因为要使用递归的思想,此时是要插入的节点。 * @param key 外部传入的key * @param value 外部传入的value * @return 返回的是新插入二叉树节点后,二叉树的跟。 */ private Node insert(Node node,int key,int value){ //如果要插入的节点是null,那么证明我们找到这个位置了,放在这即可 if(node == null){ //数量加1 mCount++; //但是接下来当是第一次插入的这个位置的时候,就返回它 return new Node(key, value); } //如果当前节点已有节点(没考虑重复吗?) //此处我们设计比较的是value的值 if(key < node.getKey()){ //此时应该在左节点递归处理.把插入的节点最终放入到了左子节点 //最终关联到左子树上. Node left = insert(node.getLeftChild(), key, value); node.setLeftChild(left); }else if(key > node.getKey()){ // //此时应该在左节点递归处理.把插入的节点最终放入到了右子节点 Node right = insert(node.getRightChild(), key, value); node.setRightChild(right); }else{ //等于的时候直接更新数值 node.setValue(value); } return node;//返回根节点 }
查询数据的实现:
/** * 根据键值来找对应的value。 * @param key 要进行查找的key * @return 返回key对应的value,如果查找失败返回null。 * */ public int serch(int key){ //调用内部函数递归的进行。 return serch(mRoot,key); } /** * * @param node 第一开始传入的是根节点,从根节点开始索引,搜索完后,传入的是下一个要搜索的节点。 * @param key 要查找的键值。 * @return 返回查找的key对应的value. */ private int serch(Node node,int key){ //证明没有找到,直接返回未找到时候的处理 if(node == null){ return (Integer) null;//?没找到返回什么比较好? } //下面就是依次对比要搜索的key和当前Node的key对应的值: // 如果相等:那证明找到了直接返回当前的值 // 如果要搜索的key小于当前节点的key:那么去当前节点的左子节点去递归的进行搜索。 // 如果要搜索的key大于当前节点的key:那么去当前节点的右子节点去递归的进行搜索。 if(node.getKey() == key){ return node.getValue(); //看它这样子key是唯一并且右边的key也大于左边?你没有猜错,哈哈哈,一开始理解错了,图里 //面都是key的值不是value }else if (key < node.getKey()){ //左侧处理,继续处理左子节点的数,找到后就直接返回。(此处理解的还是不太好) //此处这个函数就可以返回了,直接进入到下一个函数递归去查找了,这个函数的返回值就是一 //下一个函数的返回值,如此递归下去。 return serch(node.getLeftChild(), key); }else{ return serch(node.getRightChild(), key); } }
查询是否包含某个数据
/** * 判断当前的key对应的键值对是否存在二叉搜索树中 * @param key 要查找的key * @return 存在返回true,不存在返回false. */ public boolean contain(int key){ return contain(mRoot,key); } //实现思路和搜索一样,毕竟看看有没有在其实就是搜索的过程 private boolean contain(Node node,int key){ if(node==null){ return false; } if(node.getKey() == key){ return true; //看它这样子key是唯一并且右边的key也大于左边? }else if (key < node.getKey()){ //左侧处理,继续处理左子节点的数,找到后就直接返回。(此处理解的还是不太好) return contain(node.getLeftChild(), key); }else{ return contain(node.getRightChild(), key); } }
慕课网测试的时候是以,字符串为key,出现的次数为value来设计的。这种二叉树的搜索方式,比顺序在while中循环搜索块了
很多。
二叉搜索树的遍历。
遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。二叉树的遍历有三种:
前序遍历(Preorder Traversal):先访问当前节点,再依次递归访问左右子树
中序遍历
(Inorder Traversal)
:先递归访问左子树,再访问自身,再递归访问右子树
后序遍历
(Postorder Traversal)
:先递归访问左右子树,最后再访问当前节点。
上面第一种的递归访问怎么理解那?比如中序遍历,任何节点的左子节点未访问完,继续访问它的左子节点,直到左子节点完
全遍历完毕,接下来才会从最先访问完的那个节点,进行中序遍历,然后依次往上。
这三种的前序中序后序,是说的当前节点的顺序(也就是中间那个)
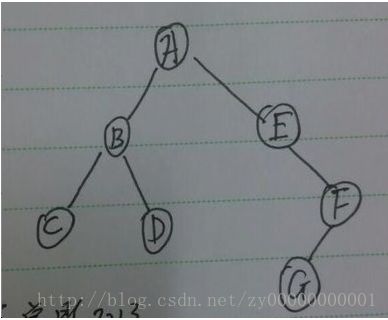
找到的百度上面的图:

前序遍历:A B C D E F G
中序遍历:C B D A E F G
后序遍历:C D B G F E A
可以看到总的来说前中后这个顺序,它是相对于当前节点的,而且还会递归深入直到最后一层的节点。然后从最下面一层
的节
点每个节点都按照某个指定的顺序依次执行。
最后一种层序遍历:按照从上到下、从左到右进行遍历。
层序遍历:A B E C D F G
前序遍历:
/** * 前序遍历 * 遍历这块就用递归的思想很容易实现,那么最小的规模就是对一个节点,函数应该带有参数Node. */ public void perTravelsal(){ //从根节点开始遍历 perTravelsal(mRoot); } private void perTravelsal(Node node){ //直到节点是null就不用再往下走了 if(node != null){ //对于每个节点都是先遍历当前节点. //遍历就进行简单的打印key值吧 System.out.print(node.getKey()+" "); //然后就去递归执行左子树,注意不用判断是否有,因为进去后自会判断 perTravelsal(node.getLeftChild()); //递归执行右子树 perTravelsal(node.getRightChild()); } }
中序遍历
/** * 中序遍历,中序遍历的一个应用就是遍历完毕后就是有序的。 */ public void inorTravelsal(){ //调用内部的递归实现. inorTravelsal(mRoot); } //具体的递归实现 private void inorTravelsal(Node node){ if(node!=null){ //先遍历左节点 inorTravelsal(node.getLeftChild()); //然后当前节点 System.out.print(node.getKey()+" "); inorTravelsal(node.getRightChild()); } }
后序遍历
/** * 后序遍历 */ public void postTarvelsal(){ //道理同前两个 postTarvelsal(mRoot); } private void postTarvelsal(Node node){ if(node!=null){ //先遍历左节点 postTarvelsal(node.getLeftChild()); //然后右子节点 postTarvelsal(node.getRightChild()); //最后才是当前节点 System.out.print(node.getKey()+" "); } }
层序遍历
/** * 层序遍历 * 我们前面提到的都是通过递归实现的深度优先遍历,只要往下的节点还有符合要求的条件,那么就会继续西先往下执行 * 而层序遍历是一种广度优先的遍历方式,先遍历根节点这一层,再遍历第二层,依次这样从上到下,从左到右. * 此处实现的思想:利用队列的先入先出的特性.(由于对队列的具体实现不清楚,暂时只理解此处的思想). * 在队列不为空的时候,开始进行操作,队列不为空那么root节点是肯定存在的,先把root * 入队,然后开始循环判断:判断条件队列为kong,先遍历处理当前节点,然后出队,(此时队列为空了) * 然后看看这个节点有没有左右子节点,如果有入队(这样就又不为空了,并且往下走了一层),左右子 * 节点处理完毕的时候.再继续循环做同样的操作。 */ public void levelTravelsal(){ //需要队列配合,先实例化一个队列 Queue<Node> queue = new BlockingQueue<Node>() { //...... }; //如果没有元素直接返回. if(isEmpty()){ return; } //有元素证明最起码root节点不为null.先入队.循环退出条件? //队列中没有元素?一层层的处理? //先把根结点入队 queue.add(mRoot); while(!queue.isEmpty()){ //只要不为空,那么就先处理当前节点,取出队列中最前面的元素. Node node = queue.poll(); //出队时做遍历操作 System.out.print(node.getKey()+" "); //当左节点不为null的时候把左节点加入队列 if(node.getLeftChild()!=null){ queue.add(node.getLeftChild()); } //当左节点不为null的时候把右节点加入队列 if(node.getRightChild()!=null){ queue.add(node.getRightChild()); } //这样至此假如当前节点有左右节点的话,队列就又不为null了, //继续循环到前面的时候,先取出最前面的节点(我们是按照左右依次放进去的), //所以下次循环的时候也是先取出当前节点出队列,遍历操作,接下来右节点出队列遍历操作, //然后继续看看有没有左右节点,这样就实现了层序遍历 } }
获取最大值和最小值
/** * 找到值最小的节点,此处返回的是找到的节点的key,毕竟用户传入的是key和value. * 找不到是返回null. * @return 值最小的节点对应的key. */ public int getMinmum(){ if(isEmpty()) return (Integer) null; //递归调用内部的实现. Node min = getMinmum(mRoot); return min.getKey(); } private Node getMinmum(Node node){ /*//不用担心node为null,以为假如是root根节点那么根本进入不到这里, //假如不是根节点的时候,在left为null的时候我们直接返回了。 Node left = node.getLeftChild(); if(left != null){ //不为null的时候递归的进行处理. getMinmum(left); }else{ //当前节点的左子节点为null,证明已经找到了最小值 return node; } return node;*/ //下面是大神的简洁代码!虽然意思一样 Node left = node.getLeftChild(); if(left == null){ return node; } //否则的话递归调用,去执行它的左子节点 return getMinmum(left); } //获取最大值节点,和最小值节点一样,根据特性 //找到右子树的最下层的子节点。 /** * 获取值最大的节点 * @return 值最大的节点对应的key. */ public int getMammum(){ if(isEmpty()) return (Integer) null; Node max = getMammum(mRoot); return max.getKey(); } private Node getMammum(Node node){ Node right = node.getRightChild(); if(right == null){ return node; } return getMammum(right); }
删除二叉搜索树的最大值和最小值.
删除最小节点
//删除二叉搜索树的最小值。此处先学习删除最大值和最小值 //因为最大值和最小值删除的时候,当前节点也就是最大/小的节点不会有两个子节点 //当时删除最小值的时候,要么当前节点没有子节点,要么当前节点只有一个右子节点。(有左子节点的时候就不是最小了) //当删除最大值的时候,要么当前节点没有子节点,要么当前节点只有一个左子节点。(有右子节点的时候也就不是最小了) /** * 从二叉树中给删除最小的节点 * */ public void removeMin(){ /*//首先应该找到最小节点 Node min = getMinmum(mRoot); if(min == null) return; //如果当前节点有右子节点,把这个节点放到最小节点的父节点的索引上 if(min.getRightChild()!=null){ //怎么得到最小节点的父节点那?此时节点我们又没有设置父节点的属性,那么就还需要一点点的查找。 //这个方案不行。 }*/ //所以只能再进行搜索,然后搜索到的时候就删除 //还需要查找,还是继续用递归比较好理解,下面调用内部的删除函数 if(isEmpty()){ return; } removeMin(mRoot); } /** * * @param node 一开始传入根节点,一次镜像操作,一值传入的是左子树上的节点, * 直到删除最小节点的时候把右子树的节点设置进来,返回给父节点。 * (其实理解的还不够好) * * @return 返回删除节点后新的二分搜索树的根,其实就是最开始传入的二叉树的节点的根. */ private Node removeMin(Node node){ Node left = node.getLeftChild(); if(left == null){//证明找到了最小节点 //开始进行删除工作,感觉java这啥也不用管啊,释放节点?, //应该先把右边的子节点拿到,无论有没有,没有就是拿到一个null嘛. Node right = node.getRightChild(); node = null;//释放当前节点的内存 mCount--;//节点数量-- //注意此处的返回值不会影响最终函数的返回值,这块的返回值仅仅是走到最小节点的时候 //把当前最小节点的右子树返回回去,然后配合(注意是在上一个函数调用中,也就是最小节点的父节点)下面 //的setLeftChild来实现把这个右子树的节点设置到父节点的左子树的节点。 return right; } //下面的递归,在没有到最小节点的时候会一直卡在此处注意不会走到return node, //卡在此处的时候然后一值传入的是当前节点的left节点,一直设置的也是left节点 //直到进入到最小节点,返回最小节点的右子节点,然后一层层设置。最后返回的是根节点root. Node temp = removeMin(left); node.setLeftChild(temp); return node; }
删除最大节点
/** * 移除最大节点,道理同移除最小节点 */ public void removeMax(){ if(isEmpty()){ return; } removeMax(mRoot); } /** * * @param node 需要进行removeMax()函数操作的当前节点. * @return 返回的是移除的节点所在的二叉树的根节点,其实就是最开始传入的二叉树的节点的根. */ private Node removeMax(Node node){ //获取右子节点 Node right = node.getRightChild(); //等于null的时候证明找到了最大的 if(right == null){ //取出来它的左子节点,无论有没有 Node left = node.getLeftChild(); node = null;//删除当前节点 mCount--; return left;//返回这个用于父节点设置右子节点 } Node temp = removeMax(right); node.setRightChild(temp); return node; }
删除任意节点:
/** * 删除任意节点:由Hibbard提出的一种方法,称为Hubbard Deletion *删除任意节点和删除最小、最大节点的区别就是,删除任意节点的时候有可能左右两个都有子节点。 *首先我们不可以简单的把左子节点或者右子节点,直接放到当前删除的节点的位置,因为这样 *很容易导致不满足二叉搜索树的特性,我们应该找到当前述的前驱或者后继放入当前位置,前驱:前面 *一个比它小的元素;后继:后面一个比它打的元素。比如一种方法,我们找到它的右子节点中所有的节点 *中的最小的节点,然后把这个最小的节点放入到删除的节点中,此时仍然满足二叉搜索树的特性,左子节点 *都小于它,右子节点都大于它。还一种中类似的就是找左子树中所有节点的最大的节点. *在找到要删除的节点时候删除步骤:(只有左子节点或者只有右子节点的时候,使用以前的,确定左右都有节点的时候) * 1、找到右子节点的最小值,删除它。 * 2、然后把这个删除的节点放到找到的这个节点位置。 * 就是把找到的节点的右子节点和左子节点分别赋值给删除的这个节点. * 3、最后这个节点还应该赋值给删除的节点的父节点的正确的位置. *以上都是通过边查找边实现的,你不能直接调用接口找到要删除的节点,这样此处无法拿到 *它的父节点无法关联. * @param key 要删除的节点的key,此处是由于我们设计key为int型 * */ public void remove(int key){ //内部还是调用递归的思想来实现 mRoot = remove(mRoot,key); } private Node remove(Node node,int key){ //第一个加入的节点,调用内部remove()的时候依然传入的是root //如果是空节点证明找到了最下层没找到. if(node == null){ return null;//直接返回空即可. } //注意是从根节点一边搜索的。 //如果发现比右子节点大,那么继续去右子节点找 if(key > node.getKey()){ //应该递归的去右边,下面整体理解的不到位。 Node right = node.getRightChild(); //继续传入右节点,此时和前面一处最大/小的理解方式是一样的, //当没有走到底,的时候是在父节点层:一直把右边的子节点传入,然后 //返回的值设置为当前有右子节点(因为这个函数返回的是当前节点,而我们传入的是右子节点) //此处一直在这循环递归直到: // 1、我们没有找到要删除的节点,那么最终会走到node == null的时候,也就是最后一层 // 返回的是null赋值给父节点的right、然后依次往上层递归返回,直到最开始传入节点那一层. // 都是在设置它们的右子节点没什么毛病.(结合上左节点一个道理) // 2、当我们找到要删除的那个节点的时候,此处假设这个节点叫D.那么再最后一层就不会走到这这个判 // 断,而会走到我们下面设计的相等时的判断中,在那个判断里面我们会返回找到的前驱或者后继,然后 // 这个节点就会被挂载到它的父节点的right子节点下。这样完成整个二叉树的链接。 Node temp = remove(right, key); node.setRightChild(temp); return node;//返回当前节点,此时是最开始传入的node。 }else if(key < node.getKey()){ //道理等同于上面 Node left= node.getLeftChild(); Node temp = remove(left, key); node.setLeftChild(left); return node; } else {//此时就是找到要删除的节点了。 //还会有三种情况: //第一种:找到的节点没有左子节点,此时就类似于删除最小值 //此时node就是代表要删除的节点 if(node.getLeftChild() == null){ //直接获取右节点,返回,让它们再去一层层赋值即可,不用管是否为null Node right = node.getRightChild(); mCount--; node = null; return right; } //第二种:找到的节点没有右子节点,此时类似于删除最大值 if(node.getRightChild() == null){ //道理同上 Node left = node.getLeftChild(); mCount--; node = null; return left; } //第三种:当左右都有子节点的时候,此时就是我们的Hubbard deletion了. //此处我们用的找删除节点的后继,也就是右子树的最小值. //所以应该先找到右子树的最小节点,复用getMinmum(node),传入当前node的右子节点。 Node min = getMinmum(node.getRightChild()); //然后复用removeMin,去删除node,此时不要传入root节点,传入当前节点的右子节点, //这样就会去删除以当前节点右子节点为根的所有子树中最小的节点的值,返回传入的右子节点. //内部会将二叉树中的那个节点的索引置为null,但我们前面拿到新索引,也是指向那个地方的. Node rightRoot = removeMin(node.getRightChild()); //正好把这个右子节的根基诶单点赋值给找到的min的右子节点 min.setRightChild(rightRoot); //然后还需要把已删除的节点的左子节点连接到找到的节点的左子节点。 //此时node就是要删除的节点 min.setLeftChild(node.getLeftChild()); node = null; //mCount--; //此时感觉会多减一个啊,在前面remove的时候减了找的那个最小的,那此时又减去当前节点 //但是把找到的最小的节点连接到二叉搜所树中的时候没有mCount++; //mCount++;//索性就不--了呗。 return min;//返回用于最前面的判断key的那两个左右子节点的判断。 } }
删除二叉搜索树的任意一个节点的时间复杂度O(logn)、顺序表中删除一个节点的时间复杂度是O(n)
3、拓展知识
关于二叉搜索树的顺序性。
前驱和后继:
关于某个数的前驱:predecessor [ˈpri:dɪsesə(r)] 前任/辈.
关于某个数的后继:
successor [səkˈsesə(r)] 继承人
对于一个数的前驱后继,是需要这个数存在的,实现前驱和后继函数时需要考虑:
1)、当前节点是否是最小值,最小值时没有前驱;同理是否为最大值,最大值没有后继。
2)、是否有左右两个子节点,如果有那么,前驱就去左子节点找最大值、后继就去右子节点找最小值。
3)、尴尬分析不出来了,左右子节点不全或者都没有时,感觉还挺麻烦,你的考虑当前节点是在父节点的那个子节点,害的
考虑父节点少子节点情况,好乱。暂不懂,不过最终也是按照key的顺序进行排列,也好找吧?
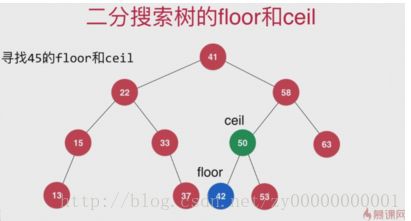
floor和ceil
floor和ceil函数不需要要查找的key存在,如果存在这两个函数的值就是返回的本身。
floor:不大于传入的key对应的值是
ceil:不小于传入的key对应的值是
floor的实现
/** * 根据传入的节点的key,来获得对应的floor操作后的节点的key * * @param key 要进行floor操作的节点的key * @return 对应的floor的结果节点的key,如果不存在返回null. */ public int floor(int key){ //如果二叉树中的mCount为0,或者小于最下值,那么没有前驱 if(mCount==0||key < getMinmum()){ return (Integer) null; } //调用内部实现的floor. Node node = floor(mRoot, key); return node.getKey(); } // 在以node为根的二叉搜索树中, 寻找key的floor值所处的节点. private Node floor(Node node, int key){ //当前节点为null的时候直接返回null. if( node == null ) return null; // 如果node的key值和要寻找的key值相等,则node本身就是key的floor节点 if( node.getKey() == key ) return node; // 如果当前node的key值比要寻找的key值大,那么就说明前驱一定是在左节点当中。 if( node.getKey() > key ) //去左节点进行递归查找 return floor( node.getLeftChild() , key ); // 走到此处的时候就是当前节点的key小于要查找的key.此时两种情况: // 1)、此时这个node就是key节点对应的floor // 2)、此时的node不是key节点对应的floor,因为在当前node的右节点中有比这个节点的key小的值。 // 也就是存在比node->key大但是小于key的其余节点. // 需要尝试向node的右子树寻找一下,总的来说理解的还是不深,但是整体感觉应该用递归的思想 // 只考虑当前节点的情况,不要试图去一层又一层的往内部进去考虑,只考虑当前时,就是去右节点再递归找找 // 如果找到了那么就返回它,如果没找到。证明当前节点(比key小)就是对的。那么就返回当前节点 Node tempNode = floor( node.getRightChild() , key ); //如果找到了证明存在比它小的直接返回小的 if( tempNode != null ) return tempNode; //走到此处的时候组恒明满足node.getKey() < key,并且在这个节点的右子树中不存在更小的了! return node; }
ceil的实现,到了等同于floor
public int ceil(int key){ //如果二叉树中的mCount为0,或者小于最下值,那么没有前驱 if(mCount==0||key > getMammum()){ return (Integer) null; } //调用内部实现的floor. Node node = ceil(mRoot, key); return node.getKey(); } private Node ceil(Node node ,int key){ //当前节点为null的时候直接返回null. if(node == null){ return null; } if(key == node.getKey()){ return node; } //当key大于当前节点的key的时候,说明应该去右子树查找,找大于key的最小值 //你不能小于key啊. if(key > node.getKey()){ return ceil(node.getRightChild(), key); } //看看左节点有没有大于key但小于当前节点的key的 Node tempNode = ceil( node.getLeftChild() , key ); if( tempNode != null ) return tempNode;//如果有返回这个 //否则返回当前节点. return node; }
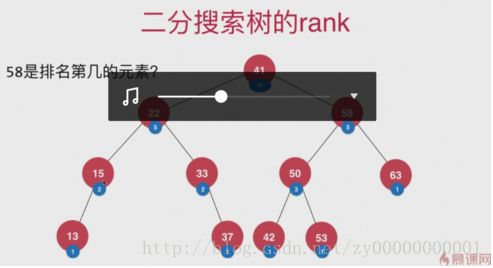
二叉搜索书的排名rank
想要知道二叉搜索树中的某个key在书中排名第几?
一种实现方法:为每个树的节点,添加一个域,这个域来标记当前节点有多少个子节点,然后就可以通过简单的逻辑和计算得
出排名第几了。
注意类似这种添加一个域记录东西的,最难的在insert和remove的时候对相应的域进行维护,一定不要忘记了。
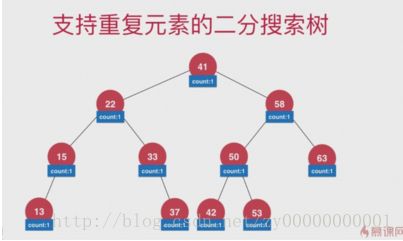
支持重复元素的二叉搜索树
第一种实现:把大于节点的放在右子节点、小于等于当前节点的放在左子节点。但这种当有大量重复元素的时候浪费空间
第二种实现:也是重新为Node加一个域,这个域用来标记当前节点的个数。
二叉搜索树的局限性。
当数据的插入顺序接近有序的时候,二叉搜索树就有可能退化成链表此时的时间复杂度从logn又变成了n
但是我们也不能一次性打乱元素,因为有可能数据时一点点你输入的,你无法拿到全部的元素。此时就改进的二叉树了:
平衡二叉树的实现有:
1)、红黑树
2)、2-3 tree
3)、AVL tree
4)、Splay tree
5)、Treap 平衡二叉树和堆的结合.
Balanced Binary Tree 具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树.
以上都是一些概念,还有很多东西要学,等第二遍的时候要深入的详细的研究了。还有trie树,单词查找树.
还有其它各种各样的树:
KD树 :(k-dimensional树的简称),是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索(如:范
围搜索和最近邻搜索)。K-D树是二进制空间分割树的特殊的情况。
区间树:区间树是在红黑树基础上进行扩展得到的支持以区间为元素的动态集合的操作,其中每个节点的关键值是区间
的左端点。
哈夫曼树:给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉
树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
各种游戏的解等就是用的二叉树的搜索